四邊形分類教學中存在問題的成因與對策

　　在討論小學數學教學問題時，我們多涉及教法與學法而較少論及教材，在論及教材時，又多涉及教材的編排與解讀而較少論及小學數學的知識體系。其實，認真鉆研教材、創造性地使用教材也是新課程理念的一個重要方面。現在廣泛使用的“人教版”小學數學教材，適當地淡化了數學概念，在第一學段的教材中很少出現數學概念的描述，但數學概念卻始終伴隨著小學數學教學，細細地鉆研、品味小學數學教材，就會發現教材中還存在著一些人們習以為常但需要進一步推敲的問題。我們在深入小學聽課的過程中，發現小學數學教師在使用教材進行分類教學時確實遇到了問題。本文中涉及的小學教材為人民教育出版社出版的小學數學教科書。
　　一、 四邊形分類教學時出現的問題
　　在《數學（四年級上冊）》中，第四單元的教學內容為平行四邊形與梯形，其中的第一部分列出了三個學習的步驟：
　　（1）畫出形狀和大小不同的四邊形。
　　（2）標出你知道的圖形的名稱。
　　（3）討論：四邊形可以分成幾類？
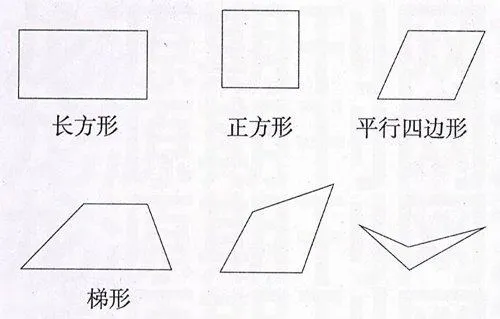
　　接著，教科書中又說：“同學們畫出的四邊形有以下幾類”。教科書中畫出了六種形狀不同的四邊形，并且在其中的四種圖形下面標注了相應的圖形名稱：
　　一方面，按照教科書的原意，四邊形可以分為長方形、正方形、平行四邊形、梯形等6類。另一方面，教科書又給出了各種四邊形之間的關系圖，采用的是集合的文氏圖，圖中顯示平行四邊形集合包含了長方形集合，長方形集合又包含了正方形集合。
　　將兩者聯系起來考慮，籠統地將四邊形分為長方形、正方形、平行四邊形、梯形等6類是錯誤的。因為我們知道，“分類”既是一個心理學概念，也是一個邏輯學概念，還是一個分類學概念，當然也是一個重要的數學概念。對于不同的教學對象，數學概念可以采取不同的呈現形式，但前后不能相悖，這是數學教學遵循的一個基本原則。因此，小學數學中無論采取怎樣的策略來進行“分類”的教學，也不能與分類的數學定義相悖。按照分類的定義，每一個四邊形必須屬于某一個類，且只能屬于其中的某一個類，不能同時屬于兩個或兩個以上的類。這樣就產生了一個邏輯問題，因為一個正方形既屬于長方形集合，又屬于平行四邊形集合，這顯然不符合分類的要求。
　　二、 問題產生的原因與對策
　　上述問題的產生，源于小學數學概念體系的不完善，許多數學對象缺乏專有的數學名詞。比如，《數學（一年級上冊）》的第四單元“認識物體和圖形”中，呈現的“長方形”不包括“正方形”，專指“長與寬不等的長方形”，但后來又把“正方形”看作是“特殊的長方形”，使“長方形”這一概念的外延進一步擴大，這就造成了在討論問題時，前后提到的“長方形”意義可能不同，有時指“所有的長方形”， 由于沒有為“長與寬不等的長方形”規定與之對應且表述簡潔的專有數學名詞，有時“長方形”又單指“長與寬不等的長方形”，這就造成了邏輯上的混亂。可以這樣設想，把“長方形”規定為“長與寬不等的長方形”的專用數學名詞，再把“長方形”與“正方形”通稱為矩形，在這一前提下，“正方形”集合就不是包含于“長方形”集合內的子集，而是包含于“矩形”集合之中，這樣就可以擺脫分類時的邏輯混亂。
　　同樣的問題還存在于“平行四邊形”的概念，最初引入的是形如“ ”的“這樣的平行四邊形”， “這樣的平行四邊形”內角都不是直角，后來又把“正方形”與“長方形”看作特殊的“平行四邊形”， “平行四邊形” 這一概念的外延也同樣擴大了，同樣在討論問題時，前后提到的“平行四邊形”意義可能不同，有時指“所有的平行四邊形”，有時又單指“這樣的平行四邊形”，同樣也造成了邏輯上的混亂。也可以這樣設想， “平行四邊形”單指“所有的平行四邊形”，而把“這樣的平行四邊形”稱為“斜平行四邊形”，同樣可以擺脫分類時的邏輯混亂，這樣還能夠引發小學生的進一步聯想，還有“直的平行四邊形”嗎？再介紹長方形、正方形都是平行四邊形就更為自然了。
　　在這樣的設想下，教科書中“四邊形的分類”略作修改就可以成立了。在形成共識之前，還有另一種規避錯誤的策略，就是把“同學們畫出的四邊形有以下幾類？”這句話改為“同學們畫出的四邊形有以下幾種類型？”。因為 “類”和“類型”是兩個不同的概念，“類”是數學概念，而“類型”是生活詞語。它們在意義上是有一定區別的。“分類”是數學方法，有嚴格的要求，而分“類型”則可以歸屬于生活的范疇，要求就相對低一些。
　　三、 四邊形的分類問題
　　四邊形的分類問題因涉及數學概念較多，是一個比較復雜的問題，在四邊形的分類過程中，長方形、正方形、平行四邊形、梯形這些概念并不一定具有同等的地位，也就是說，它們不一定能成為具有相同層級的類。
　　首先，四邊形可以按照其內角是否都小于180°分為凸四邊形和凹四邊形兩類，即內角都小于180°的四邊形為一類稱作凸四邊形；有一個內角大于180°的四邊形為一類稱作凹四邊形。教科書上畫出的四邊形中，前面5種類型的四邊形屬于凸四邊形這一類，第6種四邊形屬于凹四邊形這一類。
　　在此基礎之上，對于凸四邊形，又可以進一步地分類，按照平行邊的組數分成不規則凸四邊形、梯形、平行四邊形三類，沒有平行邊的凸四邊形稱為不規則凸四邊形，只有1組平行邊的凸四邊形是梯形，有兩組平行邊的凸四邊形是平行四邊形（這里指所有平行四邊形）。
　　由此可見，在凸四邊形的分類中，不規則凸四邊形、梯形和平行四邊形可以作為地位平等的類。因為它們都不是凹四邊形，所以它們也可以一起代替凸四邊形，成為四邊形分類中地位平等的類，但它們不能成為四邊形分類中與凸四邊形地位平等的類。因為它們都是凸四邊形集合的子集。因此，四邊形也可以分為四類：凹四邊形、不規則凸四邊形、梯形、平行四邊形。
　　對于平行四邊形，又可以按照內角中是否有直角分為有直內角的矩形和無直內角的斜平行四邊形兩類，
　　在平行四邊形的分類中，矩形和斜平行四邊形是兩個地位平等的類，但它們不能和平行四邊形成為四邊形分類中地位平等的類，因為它們都是平行四邊形集合的子集。它們可以一起代替平行四邊形，成為四邊形分類中地位平等的類。因此，四邊形也可以分為五類：凹四邊形、不規則凸四邊形、梯形、斜平行四邊形、矩形。
　　對于矩形，又可以按照鄰邊是否相等分為鄰邊不相等的矩形——長方形和鄰邊相等的矩形——正方形兩類。
　　在矩形的分類中，長方形和正方形是兩個地位平等的類，它們不能和矩形一起成為四邊形分類中地位平等的類，但它們可以一起代替矩形，成為四邊形分類中地位平等的類。因此，四邊形也可以分為凹四邊形、不規則凸四邊形、梯形、斜平行四邊形、長方形、正方形六類。
　　四邊形的分類問題確實是一個較為復雜的問題，但像教科書那樣，籠統地說四邊形可以分為那樣的6類確有不妥之處。我們應該認識到，對四邊形進行分類，對于小學四年級的學生來說，是有相當難度的，教材中提出這樣的問題，是值得我們去研究和思考的，也希望就這一問題與廣大的一線教師進行交流，以探索更為合理的解決問題的方法。當然，作為一名小學數學教師，也應該對分類及四邊形的分類問題有一個全面而深刻的認識。
　　新課程理念告訴我們，教科書只是課程的背景材料之一，廣大小學數學教師，在具體的教育教學過程中，要科學地認識教材，創造性地使用教材，同時也要敢于對教材提出質疑，不斷地進行研究，避免誤導學生，使小學數學教學日趨合理。同時也希望有關專家在修訂小學數學教材時對這些司空見慣又困擾大家的問題有所考慮，使小學數學概念體系更加完善合理。