基于填充墻對框架結構影響的抗震分析

王玨

(太原市龍城發展投資有限公司，山西太原 030000)

0 引言

從2008年的汶川地震以及過去的大量震害資料中可以看出:建筑中由于填充墻的破壞而造成的損失不可忽視。盡管填充墻常常被視為非結構構件，在體系中只起圍護與隔斷的作用而不能用來承重、抗剪。對于帶有填充墻的框架結構，規范中通常是在純框架設計的基礎上，把填充墻以荷載的形式加入結構中去，單一地考慮其周期折減，而沒有合理地考慮填充墻自身剛度對結構體系的影響。對此，基于科技工作者的研究之上，本文采用框架—填充砌體剪力墻的模型并借助于MIDAS/GEN分析軟件來研究填充墻對結構的影響。簡單的說，框架—填充砌體剪力墻模型的原理是:把填充墻看作是可以抵抗水平地震作用的剪力墻，并與框架并聯計算，且采用填充墻計算剛度，即取用填充墻自身開裂后的剛度(填充墻初始剛度值的0.2～0.3)為計算剛度。在《底層框架和后砌填充墻共同作用的試驗研究》一文中王春武等人在對先澆框架而后砌筑填充墻的試驗基礎上，研究分析了框架與填充墻共同工作的全過程及機理，提出了底層框架承擔的地震剪力設計值可以按照抗震規范所規定的方法進行計算。也就是按照底層框架剪力墻的有效剛度(框架剛度不進行折減，磚墻取其彈性剛度的20%)來進行分配。

本文采用框架—填充砌體剪力墻模型，借助MIDAS分析軟件來研究填充墻數量對框架抗震性能的影響，并與現行的規范設計方法進行比較，其中，填充墻取20%的彈性剛度作為自身的有效剛度。

1 模型的建立

為了便于計算分析，本文擬采用8層三跨的填充墻框架結構，其中X方向上的跨度均為6.3 m，Y方向上跨度分別為5.4 m，2.7 m，5.4 m，層高均為3.3 m，如圖1所示。柱子采用混凝土C35，截面尺寸為600 mm×600 mm，梁采用 C30，截面尺寸為300 mm×500 mm。假定場地類別為Ⅱ類，地震設防烈度為8度(0.2g)，分組為第一組。填充墻所取材料參數為選取混凝土空心砌塊，等級為MU15，砂漿等級為Mb7.5，厚度為240 mm，彈性模量為5 776 MPa，線性膨脹系數為10×10-6，重度為11.8 kN/m3，當填充墻以荷載形式加入結構時，梁上荷載為:11.8×3×0.24≈8.496 kN/m。

為了研究填充墻從數量上來說對框架的影響，本文采用框架—砌體剪力墻模型，考慮填充墻的剛度效應(取填充墻剛度的20%)，建立模型A(假定填充率為100%)，B(填充率75%)，C (填充率為50%)，同時為了與規范法進行對比，建立模型D與模型A進行比較。模型見圖2～圖5。

圖1 結構平面布置圖

圖2 模型A

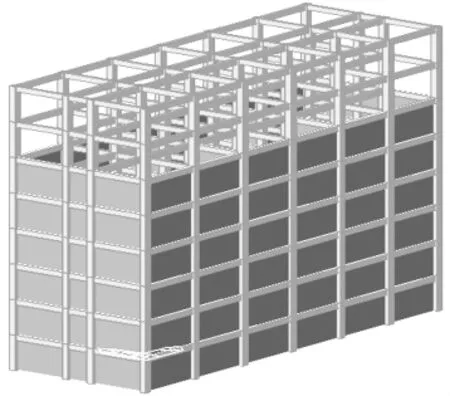
圖3 模型B

圖4 模型C

圖5 模型D

2 模型分析與結果

在MIDAS結構分析軟件中，對模型A，B，C，D進行模態分析、反應譜分析，從所得結果中選取模型A，B，C進行對比，研究填充墻的數量對框架結構的影響;選取模型A與模型D進行對比，來研究采用本文提出的框架—框架填充砌體剪力墻模型考慮剛度的方法與規范法計算結果之間的關系。

2.1 模態分析

各模型在模態分析中采用子空間迭代法，選取振型數量為12來進行分析，其自振周期結果見表1。從表1中選取A，B，C三模型的結果進行對比，并繪制圖6。選取模型A和模型D進行對比，并繪制圖7。

從表1中的計算結果以及圖6可以看出:隨著填充墻剛度效應的加入，結構自振周期減小，而且隨著填充墻的數量增大，周期降低的幅度逐漸增大。

從表1及圖7所示可以看出:模型A采用考慮剛度的方法計算的自振周期要比規范法所得結果明顯減小。

圖6 模型A，B，C周期對比圖

圖7 模型A，D周期對比圖

表1 各模型的自振周期 s

2.2 反應譜分析

模態分析下各模型的層位移、層間位移見表2及表3，并分別在層位移和層間位移上對A，B，C三個模型以及模型A和D進行對比，并且繪制圖表，見圖8～圖11。

表2 各模型的層位移 mm

表3 各模型的層間位移 mm

在模態分析中，從表2所示計算結果以及圖8中可以看出:填充墻數量不一樣的時候，層位移也不相同，對于頂層最大位移有隨著填充墻數量的增大而顯現出遞減的趨勢。從表2以及圖9中可以看出:兩種方法計算的層位移有明顯的差別，同時，本文采用的考慮剛度法計算結果要比規范法明顯小。可見填充墻的剛度效應在計算中有很大的影響。

從表3及圖10中可以看出:填充墻從數量上來說對結構層間位移的影響，模型A剛度上下比較均勻，層間位移變化比較平緩，模型B和C由于填充墻布置樓層發生變化，相應的有剛度突變現象，從而導致層間位移發生突變，突變位置分別為第六層、第四層。

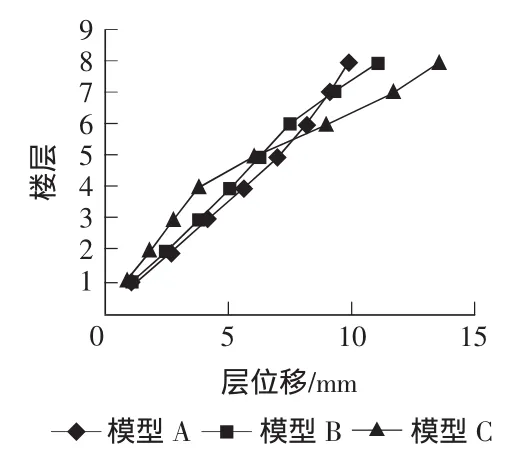
圖8 模型A，B，C層位移對比圖

圖9 模型A，D層位移對比圖

圖10 模型A，B，C層間位移對比圖

圖11 模型A，D層間位移對比圖

3 結語

通過模態分析，對各模型下的自振周期進行比較，從中可以看出:填充墻數量不同的時候，對結構周期影響也不同，而且隨著填充墻數量增多，自振周期有遞減的趨勢;兩種方法進行對比，自振周期有明顯的不同，而且考慮剛度法要比規范法計算的結果明顯減小。

通過反應譜分析，從各模型的層位移及層間位移對比來看:填充墻剛度效應的加入，對結構有明顯的影響，對于頂層位移有隨著填充墻數量增大而減小的趨勢;填充墻樓層變化處，造成的剛度突變，從而引起層間位移上明顯的突變。可見，填充墻的剛度效應在結構計算中有很大的影響，今后的工程設計中，可以對其進行合理的考慮。

［1］ 吳綺蕓，田家驊，徐顯毅.磚墻填充框架在單向及反復水平荷載作用下的性能研究［J］.建筑結構學報，1980，1(4)：38-44.

［2］ 王春武.鋼筋混凝土框架—砌體墻結構性能的試驗研究［J］.工業建筑，2002，32(7)：71-73.

［3］ 劉鳳誼，王金鳳.填充墻對結構剛度的影響［J］.山西建筑，2007，33(9)：93-94.

［4］ GB 50011-2010，建筑抗震設計規范［S］.