不憤不啟,不悱不發

楊詩鳴

啟發性教學原則是最早也是最重要的教學原則. 在我國，最早源于孔子的《論語·述而》：“不憤不啟，不悱不發.”它代表著科學、民主的教育思想，使學生更好地掌握知識、發展智力、提高分析和解決問題的能力，同時使學生得到全面發展. 所以，它有著旺盛的生命力，經久彌香.

啟發性教學原則如何在課堂上貫穿體現，如何設置數學問題與活動，如何把啟發性原則滲透于各種教學手段中，是值得廣大教師深入思考的問題，在此筆者結合人教版九年級教材中《圓周角》一課的實際教學案例談談體會與經驗.

一、引入問題

師：工廠需要生產半圓形零件，利用直角曲尺檢驗零件的凹面，如何檢測可以得到合格的零件？

通過創設情景問題，設置懸念凸現知識落差，激發學生的學習興趣，從而引入課題.

二、新課講授

理解圓周角概念：頂點在圓周上，并且兩邊都和圓相交的角叫做圓周角.

１. 概念的辨析

師：① 你認為概念中有哪些需要注意之處？② 比較圓周角概念與圓心角概念的區別與聯系.

生Ａ：頂點位置不同. 生Ｂ：角的大小不同. 生Ｃ：兩邊都與圓相交. ……

評：師在設疑中應用了以“類比”為目標的啟發方法，其特點是學生的認識活動是以確定各種對象或者現象之間在某些特征或關系上的相似為基礎的. 與學生已經熟悉的圓心角知識上，通過對與圓心角概念的比較，引導學生尋找類比物的相似屬性、現象或性質，訓練學生對知識點的遷移與聯系的思考. 加深對圓周角兩個特征：“頂點在圓上，兩邊與圓相交”的理解與記憶.

２. 通過實驗理解概念

師：讓學生自己動手制作圓周角.

生：用圖釘把橡皮筋的中間一點固定在圓上一點，再用圖釘固定橡皮筋的兩邊在圓上兩點.

師：讓學生利用自己制作的圓周角模具討論回答以下設問：

① 同一條弧所對的圓心角有多少個，圓周角又有多少個？

② 圓心與圓周角有幾種不同的位置關系？

③ 若圓心角與圓周角都對著同一條弧，彼此之間是否存在著一定的關系？

生：在圓形紙板上用圖釘固定圓上兩點，拉動橡皮筋改變頂點位置，分別置于圓心與圓上，觀察圓心角與圓周角，研究發現只要與圓的交點不變，圓周角的頂點改變位置就可以出現無數個. 還有學生興奮地說到：有無數個并且都是相等的. 很快，順著老師的問題，學生繼而發現了，有時圓心在角的內部，有時在角的外部，還會出現在角的邊上.

評：此過程應用“操作實驗”活動來體現啟發性原則，學生通過對相對抽象的數學概念的具體表現形式的操作與觀察，實現數學的發現. 同時，學生發現圓心與圓周角的三種位置關系，為后面定理的證明理下非常重要的伏筆.

三、證明定理

１. 創設特殊情景問題

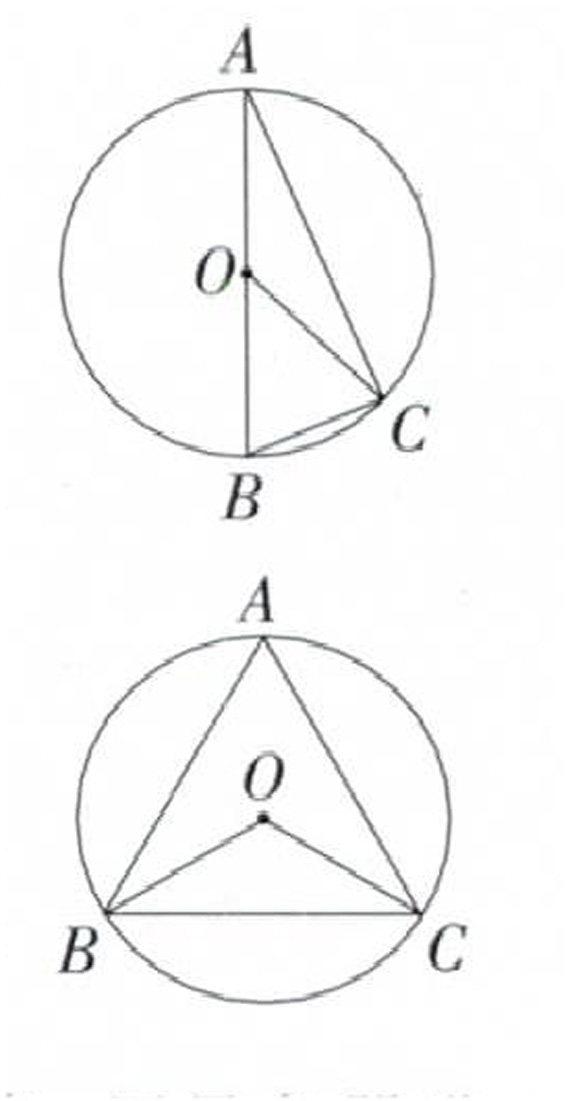
師：① 在⊙Ｏ中，∠A = 30°，∠ACB = 90°，∠BOC = （６０°）。

問：此圖中弧ＢＣ所對的圓心角與圓周角有何關系？

② 在⊙Ｏ中，有內接正三角形△ABC，∠BOC =（１２０°）.

問：此圖中弧ＢＣ所對的圓心角與圓周角有何關系？

生：通過計算得到答案后，發現圓心角是圓周角的兩倍.

２. 歸納結果，提出猜想

師：① 從特殊圖形中發現的對著同一弧的圓周角與圓心角的關系是否也存在于一般的圖形中？

生：應用自己的模具，找到圓周角與圓心角，用量角器進行大小角度的測量，接著變動頂點與交點的位置，再進行測量. 于是就有學生一邊點頭，一邊低聲討論出自己的猜想.

師：② 教師使用幾何畫板，拉動頂點位置，讓學生觀察圓周角與圓心角的大小關系，驗證猜想.

評：此過程教師采用引導學生“歸納”的方法體現啟發思想，是以歸納過程為支配地位的一種啟發方法. 立足學生的認知規律，心理特征與思維方式，采用觀察探究的教學法，滲透從特殊到一般的思想方法. 創設特殊的情景問題，作為教學的出發點，從特殊的圖形中幫助學生找準知識的連接點，啟發學生的思考方向. 同時，此過程也在引導學生進行實驗操作過程中實現啟發，讓學生發揮主觀能動性，大膽猜想.

３. 定理的證明

師：① 引導學生根據命題畫圖，寫出已知求證，再由學習小組自行討論證明.

生：由于有前面探究的基礎，學生畫圖的時候就會出現比較開闊的思路，三種情況都有同學畫出，并低聲討論到：應該要分情況討論才可以.

師：② 對三種情況的證明教師各收集一份展示給同學看，并分別由這三名同學進行講解. 然后提出：思考：“產生不同證明過程的原因是什么？”從而讓學生明白，圓周角與圓心不同的位置關系需要分情況證明.

③ 教師明確指出分情況討論的必要性與全面性.

評：此過程教師是在“演繹”定理的證明過程中體現啟發性原則的，它是以演繹過程為支配地位的一種啟發方式. 先指明學生欲要解決的問題，產生自己的問題空間，然后運用數學邏輯和抽象概括進行演繹. 指在滲透完全歸納法和分類思想，讓學生充分體會分類討論的必要性與全面性，才能真正理解此方法，突破此難點.

三、總結

此課例中，教師重組了教材的內容，為實現突破定理證明這個難點，主要在類比、實驗、歸納、演繹四種教學活動過程中，體現啟發性教學原則的應用，實現對學生學習過程的啟發、體現以學生為主體的學習思想；教師不直接地把現成的知識傳授給學生，而是引導學生自己獨立地發現相應的結果；課堂教學不是教師教學生學，而是通過教師啟發、誘導，主要依靠學習者自身的活動來實現教學目標，師生共同活動、民主相處，教學相長；學生不是消極地接受知識，而要靠自己動手、動口、動腦來獲得知識；激發學生對知識本身的興趣，并進一步培養學生對真知的探索和追求；學生在學習的過程中，感受自己的重要性，收獲成功的喜悅感.