熱毛細對流模式轉換及溫度振蕩特征

朱 鵬 段 俐 康 琦

(中國科學院力學研究所國家微重力實驗室，北京100190)

空間微重力環境為晶體生長提供了良好條件.人們開展了多次空間晶體生長實驗，結果表明雖然微重力環境基本克服了密度分層、浮力對流等對晶體生長的不利影響，但是最終生成的晶體質量不總是盡如人意.其原因在于熱毛細對流的不穩定性.在某些情況下晶體熔融體內的對流會發展為非穩態的振蕩對流，隨之而來的溫度脈動使生成的晶體內部出現和地面情況類似的條紋缺陷［1］.如何抑制振蕩熱毛細對流的產生，從而避免條紋缺陷，成為提高空間與地面晶體生長質量和效率亟待解決的問題，有必要對熱毛細對流開展深入研究.

文獻［2］利用線性穩定性分析了薄層流體熱毛細對流的熱毛細穩定性，得到2種熱毛細對流不穩定性:定常的縱向渦胞排列和非定常的熱流體波.之后，關于熱毛細對流的理論分析，文獻［3］增加考慮了重力的影響，文獻［4］考慮了自由面的熱耗散，文獻［5］考察了三維的對流流動狀態.除了理論研究，人們還對熱毛細對流進行了不少實驗研究.1998年，文獻［6］實驗研究了矩形液池中液層浮力-熱毛細對流的熱流體波以及它的各種特性.2001年，文獻［7］對不同長高比矩形液池中浮力-熱毛細對流的不穩定性進行了實驗研究.2007年，文獻［8］利用實驗和數值模擬的方法研究了薄液層中的熱流體波，并發現與液橋中的自由面溫度行波具有相似性.

熱毛細對流是空間環境中自然對流的主要形式，但是人們對其流動規律，特別是其振蕩機理的認識仍然很有限.本文的研究目標是通過實驗觀測熱毛細對流的溫度振蕩現象和數值模擬微重力條件下的熱毛細對流，分析振蕩特征和機理.研究內容包括利用熱電偶溫度測量系統，實時測量流體的溫度演變過程.然后改變實驗參數，獲得各種實驗條件下溫度振蕩的臨界條件.另外，利用flow3d數值模擬軟件，仿真微重力條件下的熱毛細對流的流動.

1 實驗模型及方法

本文作者在實驗室設計了一個熱毛細對流控制系統，圖1是該系統的簡化圖.矩形液池的右壁面是貼有電熱膜的6 mm厚的銅塊，左壁面是粘有半導體制冷片的同樣也是6 mm厚的銅塊.半導體制冷片的外面貼有散熱片能夠加速散熱.液池的前后面和底面都是6 mm厚度的K9玻璃.實驗中，實驗介質采用0.65號和1號硅油.直流電源和2個溫控儀能夠控制電熱膜和半導體制冷片的工作，從而使2個銅片之間產生溫差.隨著兩端溫差的增加，液池中硅油液層內的對流就會失穩，出現振蕩的現象.

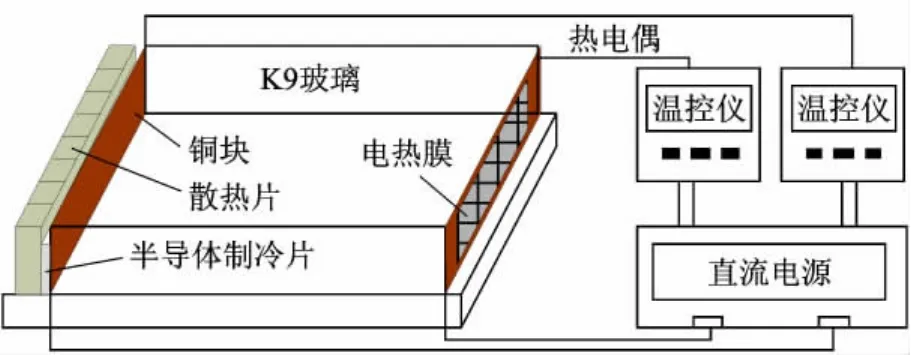
圖1 熱毛細對流控制系統

為了測量并記錄液層中流體溫度在一段時間的演變，設計了一個溫度測量系統.如圖2所示，這個系統主要由T型熱電偶、納伏表和數據采集電腦3部分組成.系統中的傳感器是直徑為60 μm的T型熱電偶.實驗中，熱電偶先將溫度信號轉變為能夠被納伏表識別的電壓信號，然后根據溫度和電動勢之間的關系演算出對應的溫度值，再實時地記錄在電腦中.該系統的分辨率可以達到0.001℃，工作時的采樣率是5 Hz.

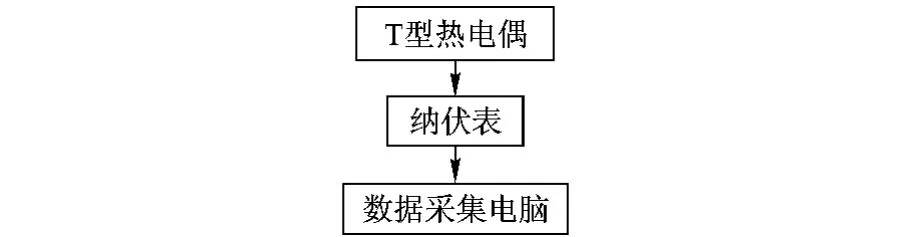
圖2 溫度測量系統

2 實驗結果及分析

對于矩形液池中液層的熱毛細對流，當兩端溫差比較小的時候，流動對應著層流的流動狀態，對應的液層中一點的溫度是一個確定的數值;隨著兩端溫差的增加，當其超過某一臨界值，流體的溫度就開始發生明顯的振蕩;隨著溫差的進一步增加，溫度的振蕩會逐漸演變為混沌，而同時流體的流動也會演變到湍流的流動狀態.本文實驗將主要關注溫度發生振蕩的臨界條件，以及起振之后溫度振蕩的一些特征.

溫度的時間曲線反應了對流的流動模式.圖3a給出了兩端溫差ΔT=12℃時，液層中測量點溫度隨時間的變化.可見，溫度只是在上下±0.01℃的范圍內隨機地變化，這些只是由于環境擾動和測量儀器導致的噪聲所引起的.所以此時應該對應著層流的流動狀態，流動還沒有發生振蕩.在圖3b中，兩端溫差ΔT=15℃，此時測量點的溫度在一個平均值附近周期性地來回振蕩，振蕩的幅度達到±0.05℃.所以此時應該對應了對流第一次模式轉變之后的流動狀態.圖3c中，當液層兩端溫差達到ΔT=43℃時，流體的溫度振蕩變得不再規則，振幅達到±1℃.此時，液層的流動已經發展到湍流的流動狀態.

圖3給出了臨界溫差前后溫度的時間曲線，逐漸縮小范圍就可以得到臨界溫差.在實驗中，對0.65號和1號硅油進行了溫度振蕩的觀察，得到了不同液層厚度條件下溫度振蕩的臨界條件，見表1.對于6 mm高的液池，本文只是在一定的液層厚度范圍內觀察到溫度的振蕩.當厚度太小，液層內部很難建立比較好的流動;當厚度太大，自由面很接近液池頂部，液體很容易順著直角和蓋子爬出液池.

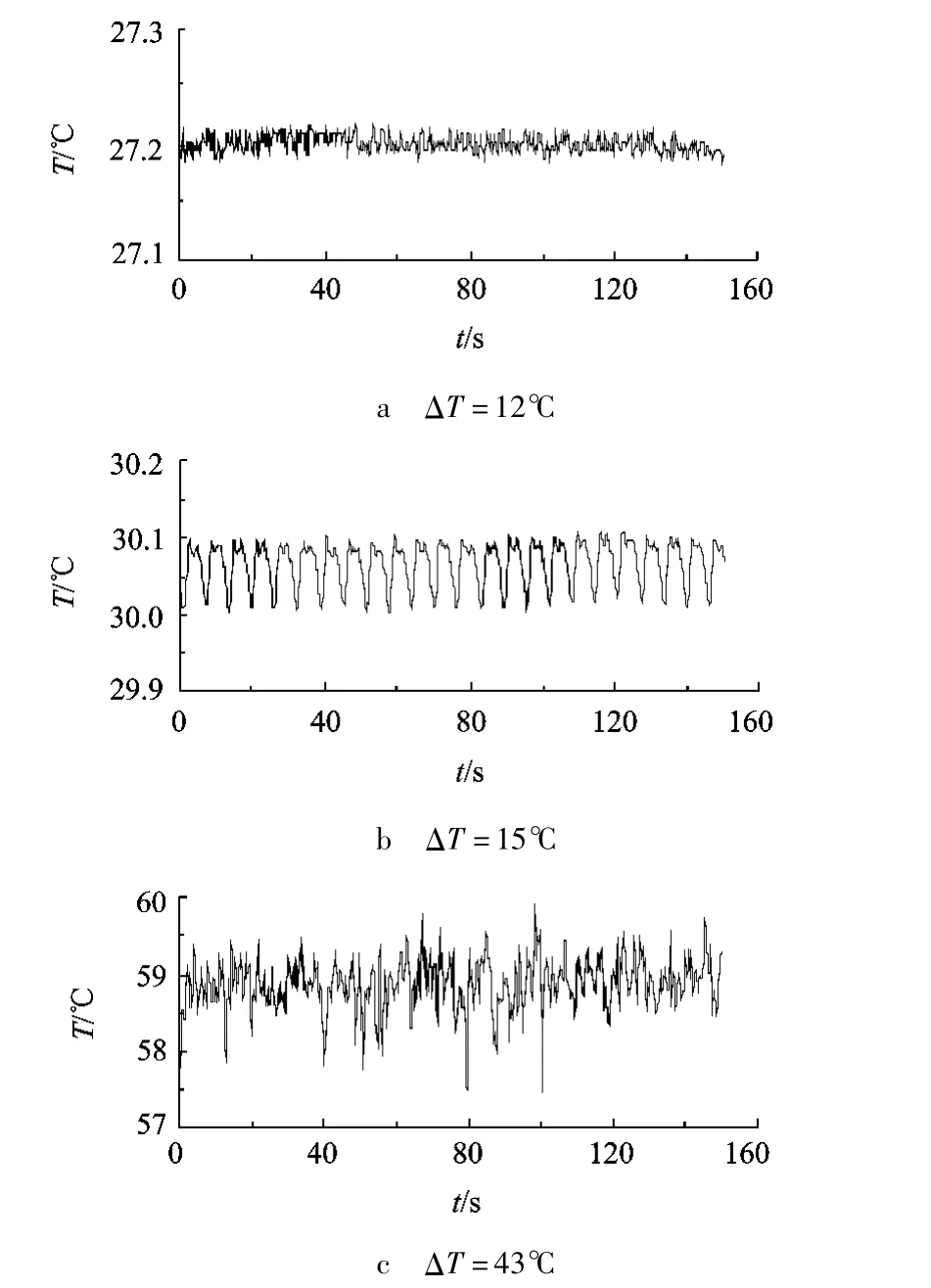
圖3 溫度曲線

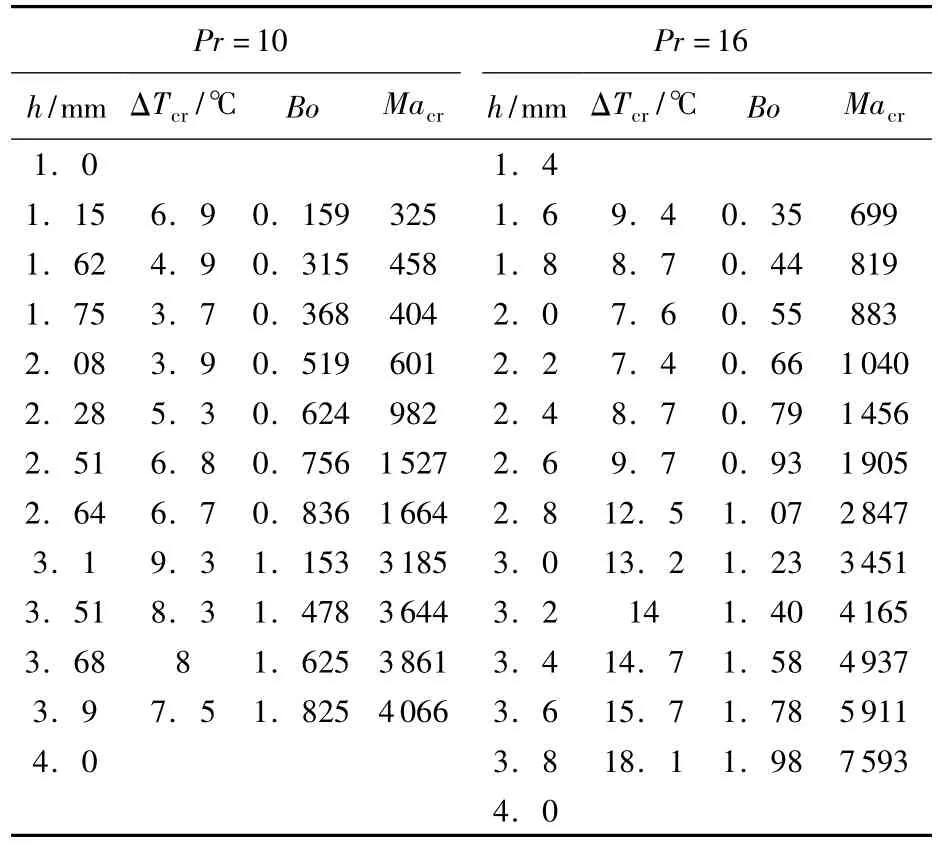
表1 0.65號和1號硅油臨界條件

為了對實驗結果進行討論，把實驗條件無量綱化.用式 (1)來表征溫度振蕩的起振，用式(2)來描述重力和熱毛細力的相對強弱.

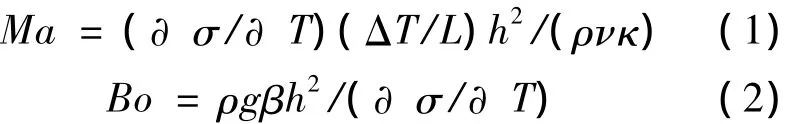
式中，σ為表面張力;T為流體溫度;L為液層橫向長度;ρ為實驗流體密度;ν為實驗流體動力粘度;κ為熱擴散系數;g為重力加速度;β為熱膨脹系數;Bo為Bond數.

圖4給出了2種硅油Macr-Bo曲線.可見，對于同一種硅油，Macr隨著Bo的增加而變大，說明重力的增強使對流的流動變得更加穩定.對比2種Pr的硅油，當Bo＜1.2時，兩者的變化曲線基本一致;當Bo＞1.2時，對于同樣的Bo，高Pr的硅油對應的Macr更大，即高Pr的硅油更加穩定.

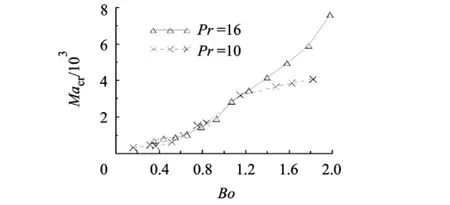
圖4 0.65號和1號硅油Macr-Bo關系曲線

在一些數值模擬結果［9］中，包括本文用flow3d的仿真結果，熱流體波都是先在某些局部區域起振，然后才擴展到整個流場.為了檢驗這種現象，實驗中用2套設備同時測量并記錄了液層中不同位置的溫度振蕩.由圖5可見，隨著兩端的連續升溫，測量點的溫度也會增加，隨后都會發生溫度的振蕩.為了更加清楚地觀察它們的起振過程，用小波變換的方法從原始信號中提取出溫度振蕩的信號.從2個測量點的振蕩信號可以看到，它們幾乎是同時起振.實驗中，當任意更換2個測量點的位置，也都是同樣的結果.由此可以得到，在實驗中，液層中的熱毛細對流一旦發生溫度的振蕩，整個流場范圍內幾乎同時起振.

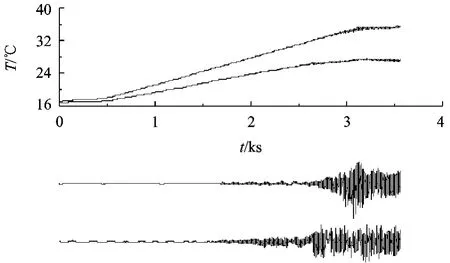
圖5 不同位置溫度振蕩對比

3 數值模擬結果及討論

為了探討微重力條件下的熱毛細對流，用flow3d軟件數值模擬了零重力時相同尺寸液池中熱毛細對流的流動狀況，發現了一種自由面晃蕩的現象.在一開始溫差建立的階段，在自由面，由于水平溫度梯度引起的表面張力梯度會驅使自由面的流體從熱端流向冷端.由于缺少了重力的下拉作用，流體會明顯地在冷端堆積，從而使自由面產生明顯的變形.在經歷了一段時間充分發展之后，自由面就發生一種晃蕩的現象.如圖6所示，它給出了橫向自由面變形在半個周期內的變化情況.自由面大概以中間的虛線為平衡位置來回地晃蕩.本文認為這種晃蕩的現象主要是由自由面的變形和液層流場的相互作用導致的.當自由面到最大變形處時，熱端液層變薄，流體運動到冷端時的流速變小，流速對應的動壓不足以與自由面的張力相平衡，自由面就會趨向平衡位置.隨著自由面變形的減小，液層內部的流速又會恢復，直到自由面越過平衡位置到達最小變形處，恢復的流速對應的動壓又會使自由面加大變形.如此反復，就會產生這種自由面晃蕩的現象.

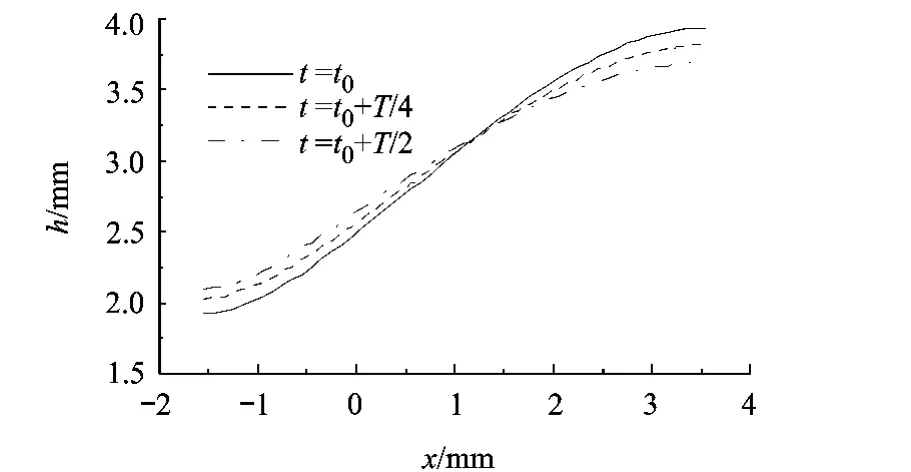
圖6 自由面變形

圖7是提取出微重力條件下熱毛細對流演變過程中冷端接觸點位置隨時間的變化.可見，對于3 mm厚度的液層，自由面的最大偏移是1.2 mm，晃蕩的振幅達到0.2 mm，周期約為6.5 s.圖8是相同條件下液層中某一點的溫度隨時間的變化.同樣可見，振蕩的周期也約為6.5 s，振幅達到0.18℃.

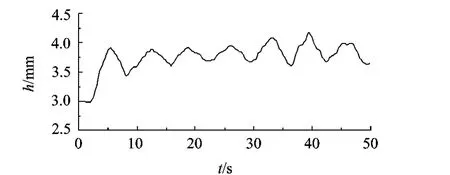
圖7 冷端接觸點偏移

圖8 微重力條件下熱毛細對流溫度振蕩

4 結論

本文通過實驗和數值模擬的方法研究了矩形液池中由于自由面水平溫度梯度導致的熱毛細對流.首先定量地測量了各種穩態條件下熱毛細對流液層中溫度的演變過程，觀察到了熱毛細對流的溫度振蕩現象，并且獲得了各種實驗條件下溫度振蕩的臨界條件，討論了它與Pr和Bo之間的關系.與很多數值模擬結果不同的是，實驗中溫度的振蕩在整個流場中幾乎同時起振.另外，數值模擬了微重力條件下的熱毛細對流，發現了一種由自由面變形和液層流場相互作用導致的晃蕩的現象.

References)

［1］Jakeman E，Hurle D T J.Thermal oscillations and their effect on solidification processes［J］.Review of Physics in Technology，1972，3(1):3－30

［2］Smith M K，Davis S H.Instabilities of dynamic thermocapillary liquid layers part 1:convective instabilities［J］.Journal of Fluid Mechanics，1983，132(7):119－144

［3］Parmentier P M，Regnier V C，Lebon G.Buoyant-thermocapillary instabilities in medium-prandtl-number fluid layers subject to a horizontal temperature-gradient［J］.International Journal of Heat and Mass Transfer，1993，36(9):2417 －2427

［4］Mercier J F，Normand C.Buoyant-thermocapillary instabilities of differentially heated liquid layers ［J］.Physics of Fluids，1996，8(6):1433－1445

［5］Kuhlmann H C，Albensoeder S.Three-dimensional flow instabilities in a thermocapillary-driven cavity［J］.Physical Review E，2008，77(3):036303

［6］Riley R J，Neitzel G P.Instability of thermocapillary-buoyancy convection in shallow layers part 1:characterization of steady and oscillatory instabilities ［J］.Journal of Fluid Mechanics，1998，359(3):143－164

［7］Burguete J，Mukolobwiez N，Daviaud F.Buoyant-thermocapillary instabilities in extended liquid layers subjected to a horizontal temperature gradient［J］.Physics of Fluids，2001，13(10):2773－2787

［8］Kawamura H，Tagaya E，Hoshino Y.A consideration on the relation between the oscillatory thermocapillary flow in a liquid bridge and the hydrothermal wave in a thin liquid layer ［J］.International Journal of Heat and Mass Transfer，2007，50(7/8):1263－1268

［9］Tang Z M，Hu W R.The hydrothermal wave of large-Prandtlnumber fluid in a shallow cavity［J］.Science in China Series G:Physics，Mechanics ＆ Astronomy，2007，50(6):787－796