守恒律方程的導數人工壓縮法

董海濤 劉福軍 韓 沖

(北京航空航天大學 航空科學與工程學院，北京100191)

流體力學方程組解的間斷性在早期是一個主要難點，所有二階以上的經典格式 (如 Lax-Wendroff格式)在激波等間斷處會不可避免地出現偽振蕩.之后，由于TVD(Total Variation Diminishing)判據及限制器技術的出現，產生了一批無振蕩高精度格式，如TVD，ENO(Essentially Non-oscillatory)，NND(Non-Oscillatory and Non-free-parameter Dissipation)，無振蕩緊致格式、熵條件格式等，統稱為高分辨率格式，對激波的模擬取得了較好結果.許多復雜流動問題，流動參數變化劇烈，除可能存在激波間斷外，還有帶極值點的渦結構等，尤其對低速問題 (定常)沒有激波間斷，更多的 (高雷諾數)是極值點.而現有高分辨率格式若嚴格要求無振蕩，則都存在極值點精度退化問題，為了更好地模擬復雜流動問題，須考慮提高極值點處的精度.目前，對這個問題的研究還較少，本文提出的導數人工壓縮，就是為了解決20世紀80年代以來這些高階格式在極值點降階的問題，以提高對極值點的分辨率.本文先進行了導數人工壓縮方法的推導，并構造了人工壓縮和導數人工壓縮結合的混合格式，然后用單個標量方程的多極值間斷初值問題和Shu-Osher激波管算例進行了數值驗證，極值點處的精度得到較好的改善.

1 導數人工壓縮法的思想和推導

1977年文獻 ［1］提出人工壓縮方法并在1983年用于Harten-TVD［2］格式，以提高接觸間斷分辨率，本文受此啟發，獲得了導數人工壓縮方法構造思路.考慮守恒律方程初值問題

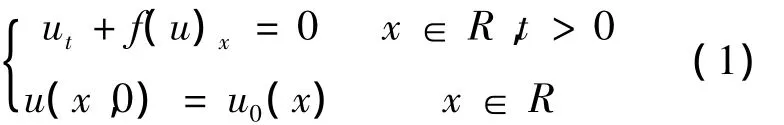
1.1 Harten的人工壓縮法

Harten的原始二階TVD格式為

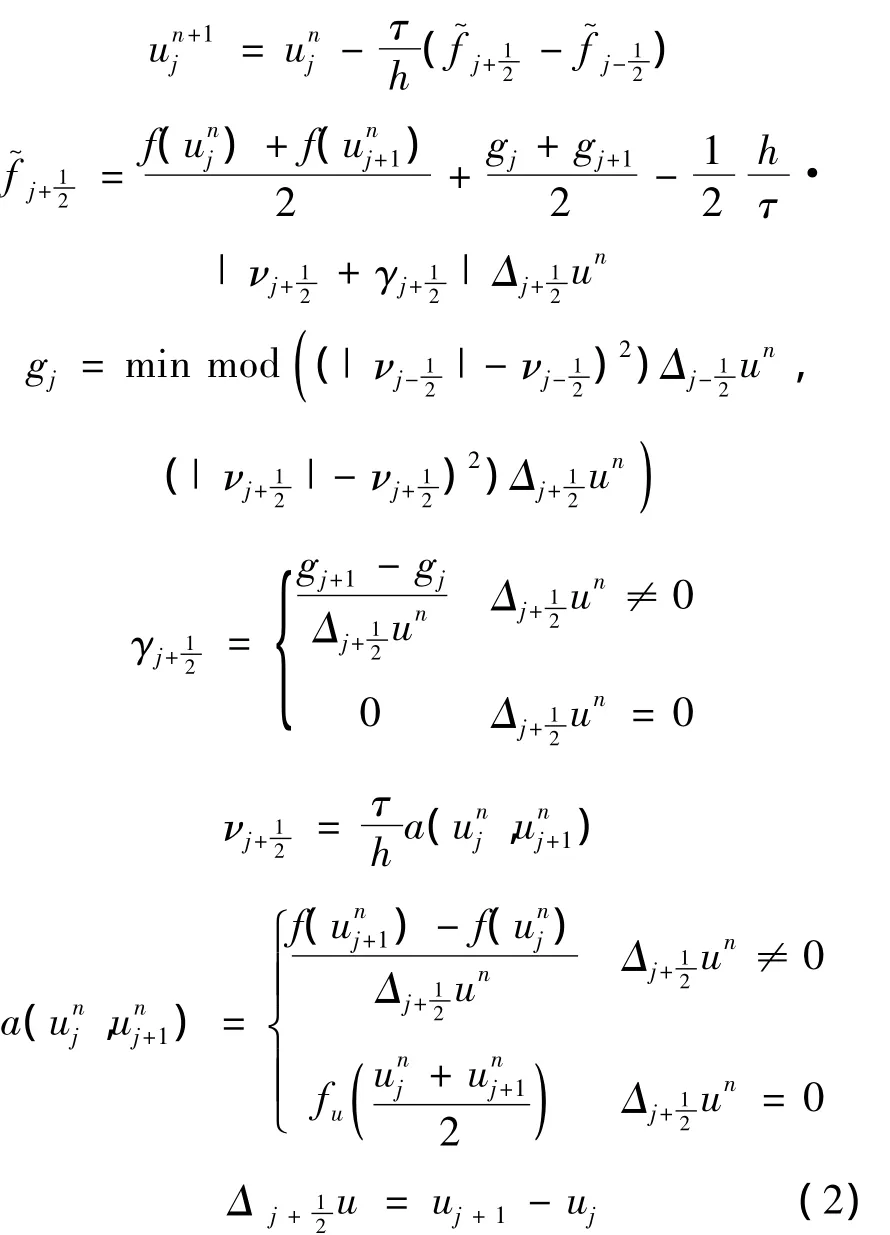
其中絕……