交替LU分裂算法及其在CFD中的應用

相 倩 吳頌平

(北京航空航天大學 航空科學與工程學院，北京100191)

徐 悅

(中國航空研究院 航空數值模擬技術研究應用中心，北京100012)

隨著CFD(Computational Fluid Dynamics)模擬能力的提高，計算中需要求解的方程組的規模也急劇增加.快速求解大型方程組已經成為CFD計算的瓶頸之一［1］.迭代算法是求解大型方程組的有效方法，其收斂速度依賴于方程組系數矩陣的性質.針對超聲速流動離散方程組系數矩陣往往是本質正定的這一特點，本文提出了一種迭代算法，稱為交替LU分裂 (ALUS，Alternating Lower-Upper Splitting)算法.該算法計算量小，易于實現，且具有很好的魯棒性，可大大節省計算時間.

1 迭代算法

常用的迭代算法分為兩類.一類是基于系數矩陣分裂的古典迭代方法，例如Jacobi方法，Gauss-Seidel方法，松弛法 (SOR，Successive O-ver Relaxation)等.其中交替方向算法因其簡單容易實現，在實際計算中有著廣泛的應用［2］.近些年逐步發展起來的HSS(Hermitian and skew-Hermitian Splitting)方法［3］和 PSS(Positive definite and skew-Hermitian Splitting)方法［4］及其擴展算法也可以看作是廣義的交替方向算法，具體參見文獻［5］.另一類算法是基于變分極值原理的迭代算法，其中最具代表性的有適用于對稱正定系統的共軛梯度法 (CG，Conjugate Gradient)以及適用于非對稱正定的廣義極小殘量法 (GMRES，Generalized Minimal Residual).

1.1 交替方向算法

設矩陣A∈Cn×n，考慮線性方程組

若A可以分解成A=Q+S，則迭代算法

稱為交替方向算法.該算法亦可以寫成

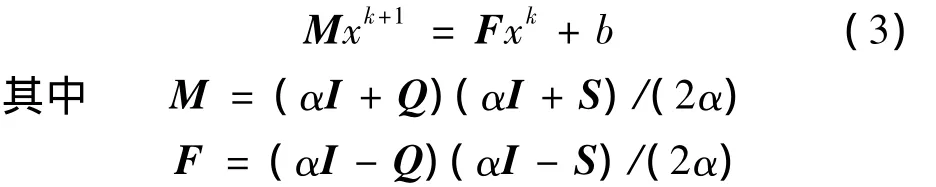
并且A=M－F.由式 (3)可知，矩陣M可以看成是一個預處理算子.一個好的預處理算子M應該構造簡單易于求逆，并且譜半徑ρ(M－1F)應該盡可能小.

對于交替方向算法式 (2)，有以下定理成立.

定理1 對任意的正實……