基于混合可靠性分析的協同優化方法

王星皓 馬紀明 曾聲奎 趙雪梅

(北京航空航天大學 可靠性與系統工程學院，北京100191)

多學科設計優化(MDO，Multidisciplinary Design Optimization)是工程領域一種新的優化設計方法，其主要思想是通過充分利用各個學科之間相互作用的協同效應，獲得系統整體的最優解［1］.目前，MDO已經廣泛地應用于航空航天、機械制造等領域.其中，協同優化方法(CO，Collaborative Optimization)是 Kroo［2］等人在一致性約束優化算法基礎上提出的一種多級MDO算法，由于其結構簡單且算法收斂性比較可靠，因此得到了較廣泛的重視和應用.在MDO中，當輸入變量發生波動，仿真模型產生不確定性時，系統的輸出和學科間的耦合也就成為了隨機變量，就產生了如何取得MDO可行解的問題，解決這樣的問題稱之為基于可靠性的多學科設計優化(RBMDO，Reliability-based Multidisciplinary Design Optimization).

國內外眾多學者對RBMDO中高效的可靠性分析方法和協調方法進行了研究.文獻［3］提出了用系統輸出的響應面模型代替高計算成本的約束函數，基于響應面約束來進行最可能點(MPP，Most Probable Point)的搜索;文獻［4］使用 ATC(Analytical Target Cascading)算法將RBMDO分解為多個基于可靠性的設計優化(RBDO，Reliability-based Design Optimization)問題，對每個RBDO問題采用順序優化與可靠性分析(SORA，Sequential Optimization and Reliability Assessment)方法來解決;文獻［5］提出了采用并行子空間方法的RBMDO方法，利用并行子空間來進行MPP的搜索和整個問題的優化;文獻［6］等提出了一種MDO框架下的SORA方法，實現了可靠性分析與多學科優化的解耦;文獻［7］提出了一種基于改進一次二階矩方法的并行子空間優化方法，該方法由于不在優化過程中執行MPP的計算，因此效率更高.文獻［8］等提出了可靠性分析的分層混合策略，在MDO的頂層和底層采用不同的可靠性分析方法，從而提高可靠性分析的效率.

針對不確定性MDO中計算成本高的問題，本文將協同優化方法與兩種在計算精度和成本上各有優勢的可靠性分析方法相結合，提出一種基于混合可靠性分析的協同優化方法.該方法在傳統嵌套循環算法的基礎上，通過估算優化迭代點與約束邊界的距離，選擇精度不同的可靠性分析方法，僅對靠近約束邊界的點進行基于一次可靠性方法(FORM，First Order Reliability Method)的可靠性分析，其余點僅采用均值法粗略計算其可靠度.從而在保證分析精度的前提下，避免了在優化初期高成本的可靠性分析，有效地降低了計算成本，提高了計算效率.

1 現有可靠性分析方法

1.1 均 值 法

均值法［9］是在機械結構可靠性研究初期提出的一種方法，其基本思想是首先將非線性狀態函數在隨機變量的均值點處作泰勒級數展開并保留至一次項，近似計算狀態函數的平均值和標準差.

假設狀態函數g(X)是光滑的并且在均值處可以泰勒展開，在均值點處的狀態函數可以表示為

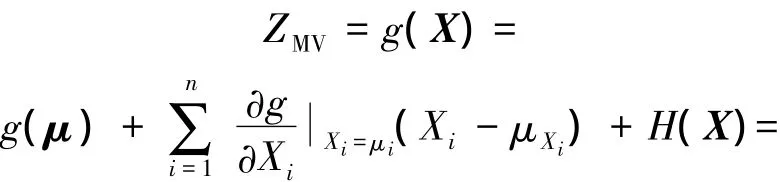
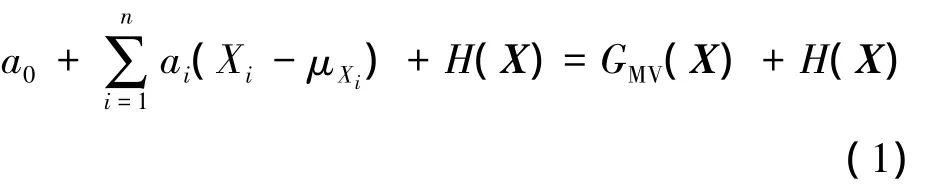
式中，GMV代表一次項之和;H(X)代表高階項系數ai通過數值微分或者最小平方法來計算，用數值微分方法估算Z函數，最少次數為n+1次.

只保留一次項，假設都為獨立隨機變量，Z的均值和方差可以近似為

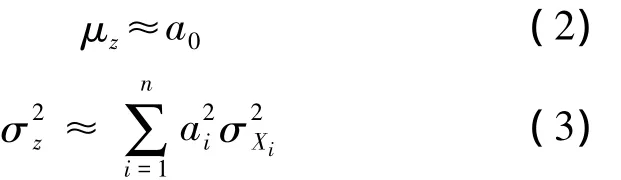
可靠性指標可以表示為

從計算可靠性指標所需的系統分析次數來看，該方法是約束可靠性分析中效率最高的.但對于非線性的狀態函數，均值法計算結果不夠精確.

1.2FORM 法

1974年 Hasofer和 Lind［9］更加科學地對可靠性指標進行了定義，并引入了驗算點的概念，提出了改進的FORM方法.該算法使用當量正態法將狀態函數g(X)變換為g'(u).此時，設計驗算點u*到坐標原點的距離為坐標原點到極限狀態曲面(g(u)=0)的最短距離β，定義該值為可靠性指標.驗算點法算法步驟為:

1)假定初始驗算點.

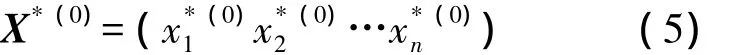
2)根據設計驗算點，計算非正態隨機變量的等效正態分布參數.

3)計算可靠性指標.

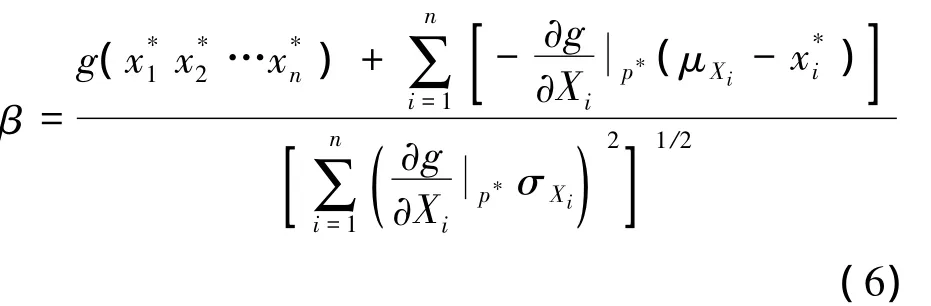
4)計算重要度系數.

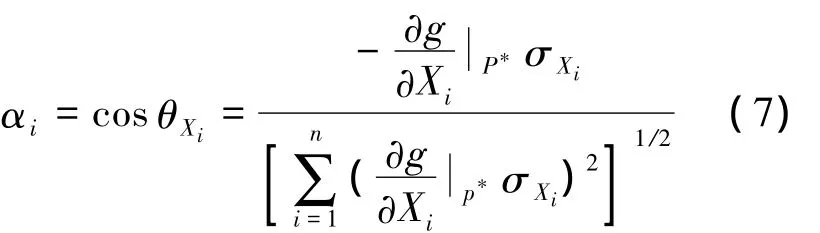
5)計算新的驗算點.

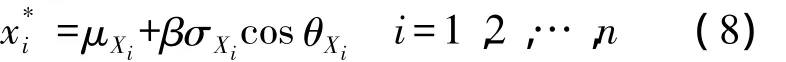
FORM法能對可靠性指標進行精度較高的計算，是一種應用較為廣泛的可靠性分析方法，但其計算成本較高.

2 基于混合可靠性分析的協同優化

本文提出的基于混合可靠性分析的協同優化方法是在標準的協同方法上提出的，仍具有協同優化各個學科自治性較高的優點，并針對每個子學科進行基于可靠性的設計優化過程進行了改進.

基于混合可靠性分析的協同優化方法的數學模型可描述如下:

系統級優化問題:

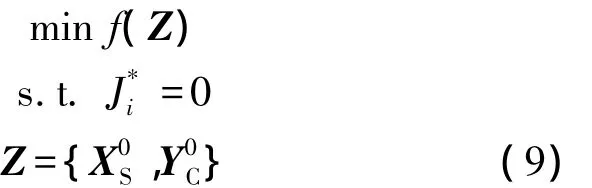
式中，f(Z)是整個系統的目標函數;Ji是第i個一致性等式約束，也是第i個子系統的目標，系統級設計變量包括學科之間的共享設計變量{}和學科間的耦合狀態變量{}.

子系統的優化模型為:

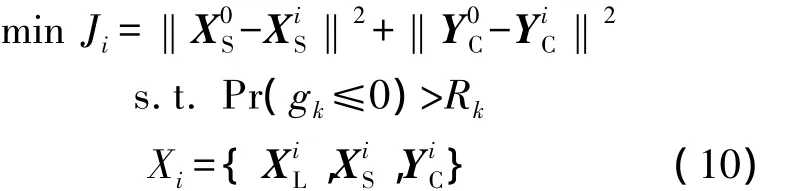
式中，gk表示第p個可靠性約束條件;Rk為該可靠性約束的可靠度要求，子系統級的設計變量包括該子系統的局部設計變量{}、共享設計變量{}和耦合狀態變量{}.

考慮到優化過程是一個從初始點逐步迭代，收斂到約束邊界的過程，通過每次分析得到的可靠性值來判斷該設計點與約束邊界的距離，并以此為依據在下一迭代點的可靠性分析中選擇合適的算法.通過在遠離邊界時選用效率較高的均值法，在邊界附近選用精度較高的FORM法，在不影響最終優化結果可靠性精度的前提下，提高了效率.基于混合可靠性分析方法的系統級優化與標準的協同優化過程基本相同，其子系統進行優化的流程如圖1所示.

1)在初始點處使用均值法進行粗略的可靠性分析，得可靠度R0;

2)初始點一般無法滿足收斂條件，優化迭代產生新的設計點;

3)在對新的設計點進行可靠性分析之前，通過判斷上次可靠性分析的結果來選擇本次可靠性分析的方法.若滿足|Rn－1－Rreq|＜ε 且Rn－1≠1，則轉步驟4)，否則轉步驟5).其中Rreq為該可靠性約束的可靠度要求，ε為均值法分析可能產生的最大誤差，實際工程中可以根據經驗取值;

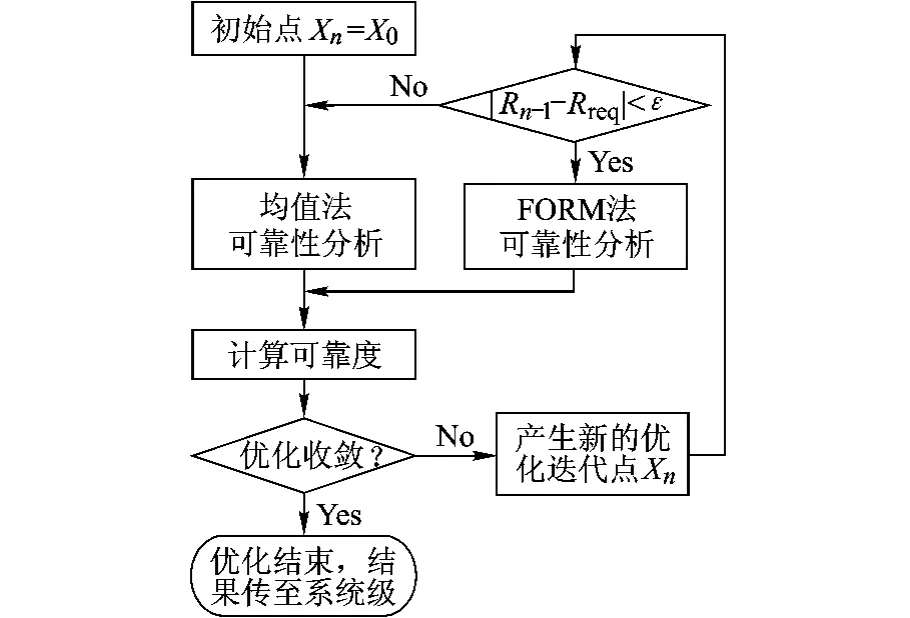
圖1 子系統級優化流程

4)采用FORM法進行可靠性分析，計算可靠性指標

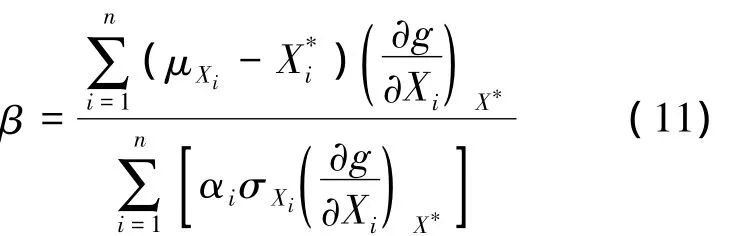
式中，Xi為經多次迭代得到的MPP點，轉步驟6);

5)采用均值法進行可靠性分析，計算可靠性指標為

式中，μz和σz為用近似方法得到的均值和方差，轉步驟6);

6)計算可靠度

式中Φ(·)為標準正態分布函數;

7)判斷本次優化是否滿足收斂條件及可靠性約束，若滿足就結束子系統級優化，否則優化迭代產生新的設計點，轉步驟3)，繼續優化和可靠性分析，直至滿足收斂條件為止.

3 算例試驗

減速器優化算例是 NASA(National Aeronautics and Space Administration)評估多學科設計方法性能的10個標準算例之一［10］.減速器多學科設計優化的目標是在滿足減速器中轉軸和齒輪大量約束的同時，使得減速器體積最小(即質量最輕).該優化問題有7個設計變量，其中x1為齒面寬度，x2為齒輪模數，x3為小齒輪齒數，x4，x5為軸承間距，x6，x7為大小齒輪軸的直徑.

數學模型為

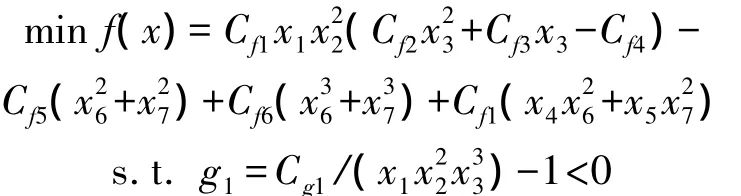
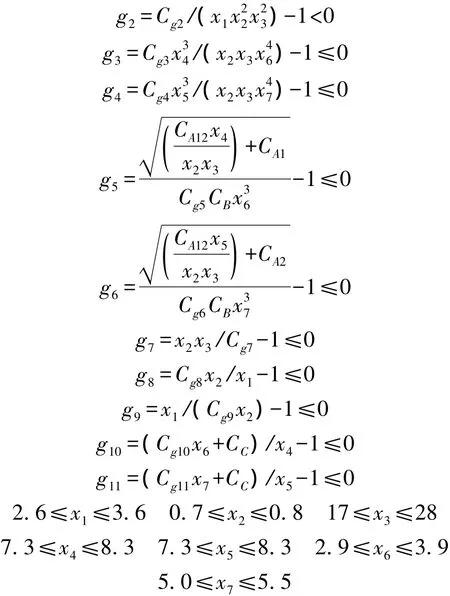
其中，g1為輪齒的最大彎曲應力;g2為輪齒最大接觸應力;g3和g4為軸的橫向最大撓度;g5和g6為軸內最大應力;g7，g8和g9為尺寸和空間限制;g10和g11為軸尺寸計算的經驗公式.為了驗算本文提出的算法，將x1－x2，x4－x7作為服從正態分布的隨機變量，將g1－g4作為可靠性約束，取可靠度要求為95%，建立基于可靠性的協同優化數學模型，分別采用均值法、FORM法以及混合可靠性分析方法來進行可靠性分析.

系統級優化模型為

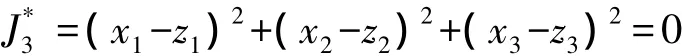
子系統1優化模型為

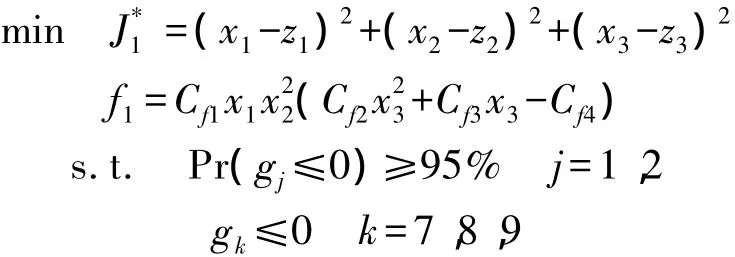
子系統2優化模型為

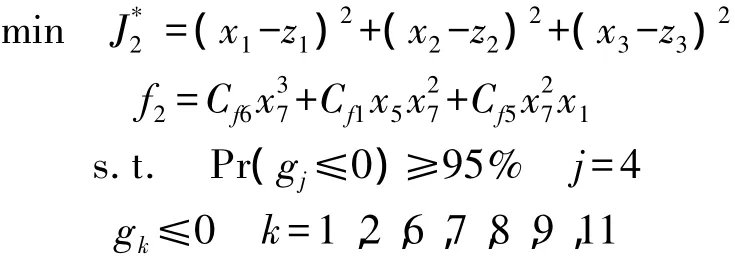
子系統3優化模型為

在優化過程中，系統級變量設為確定性變量，子系統級為服從實際分布規律的隨機變量，分別以各設計量的上下限的中值點作為初始點，分別采用不同的可靠性分析方法進行優化，其計算成本和優化結果如表1和表2所示，并對約束的可靠性采用Monte-Carlo方法進行了分析，各個約束可靠性分析結果如表3所示.

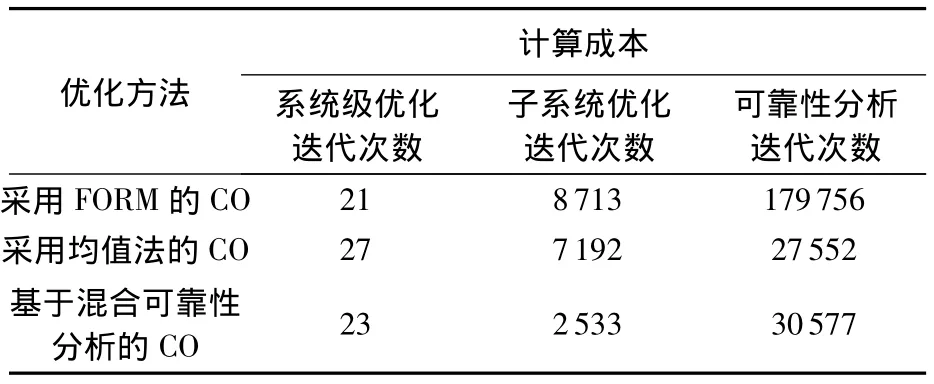
表1 循環次數對比

表2 優化結果對比

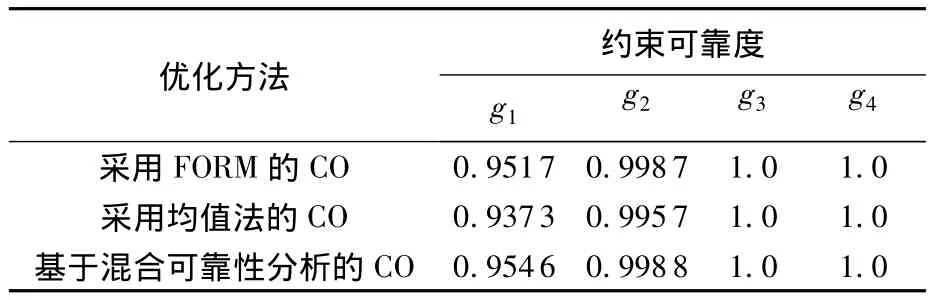
表3 約束的可靠性分析

可以看到采用均值法的CO方法雖然計算成本較低，但部分約束(如本例中g1)不滿足可靠性要求.基于混合可靠性分析的CO與采用FORM方法的CO得到的優化結果都滿足要求，但基于混合可靠性分析的CO計算成本更低.

4 結論

1)將協同優化與兩種基本可靠性分析方法相結合，提出了基于混合可靠性分析的協同優化的數學模型和計算流程，并通過算例驗證其可行性.

2)基于混合可靠性的協同優化方法在保證可靠性精度的同時，有效減少了計算成本，有一定的工程應用價值.

References)

［1］Sobieszczanski-Sobieski，J，Haftka R T.Multidisciplinary aerospace design optimization:survey of recent developments［J］.Structural Optimization，1997，14(1):1－23

［2］Kroo I M，Manning Valerie.Collaborative optimization:status and directions［C］//Proc ofthe 8th AIAA/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization.Long Beach:AIAA，2000

［3］Sue R H，Oakley D R，Rhodes G S.Multidisciplinary stochastic optimization［C］//Proc of the 10th Conference on Engineer Mechanics Part 2，Vol 2.Boulder，CO:ASME，1995:934－937

［4］Liao G，Kim H M，Ha C.Multilevel optimization considering variability in design variables of multidisciplinary system［C］//Proceedings of the 11th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization.Portsmouth，Virginia，USA:AIAA，2006

［5］Padamanabhan D，Batill S M.An iterative concurrent subspace robust design framework［C］//Proc of 8th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization.Long Beach，California:AIAA，2000:133－138

［6］Fan Hui，Li Weiji.An efficient method for reliability-based multidisciplinary design optimization ［J］.Chinese Journal of Aeronautics，2008，21(4):335－340

［7］Du Xiaoping，Guo Jia，Beeram Harish.Sequential optimization and reliability assessment for multidisciplinary systems design［J］.Struct Multidisc Optim，2008，35:117－130

［8］Li Liansheng，Jing Shikai，Liu Jihong.A hierarchical hybrid strategy for reliability analysis of multidisciplinary design optimization［C］//Proceedings of the 2010 14th International Conference on Computer Supported Cooperative Work in Design.Shanghai:IEEE，2010:525－530

［9］張建國，蘇多，劉英衛.機械產品可靠性分析與優化［M］.北京:電子工業出版社，2008

Zhang Jianguo，Su Duo，Liu Yingwei.Reliability analysis and optimization of mechanical products［M］.Beijing:Publishing House of Electronics Industry，2008(in Chinese)

［10］Kodiyalam S.Evaluation of methods for multidisciplinary design optimization(MDO)，PhaseI［R］.NASA/CR-1998-208716，1998