一個多介質流體的Baer－Nunziato修正模型及其Lax－Wendroff格式

吳 強， M.A.烏拉赫

（1.上海大學 數學系，上海 200444；2.合肥工業大學 數學學院，安徽 合肥 230009；3.吉大港大學 數學系，吉大港 4331，孟加拉國）

一個多介質流體的Baer－Nunziato修正模型及其Lax－Wendroff格式

吳 強1，2， M.A.烏拉赫3

（1.上海大學 數學系，上海 200444；2.合肥工業大學 數學學院，安徽 合肥 230009；3.吉大港大學 數學系，吉大港 4331，孟加拉國）

文章在BN模型基礎上，提出了一個描述可壓縮多介質流體的介質界面的修正模型，并且給出了該模型的具有二階精度的Lax－Wendroff格式。無論模型和格式，都保證了總質量和分質量守恒、總動量和總能量守恒。更重要的是它消除了速度和壓力在介質界面處的偽振蕩，數值算例表明這一算法是有效的。

守恒律；多介質流；偽振蕩；Lax－Wendroff格式

可壓縮多介質流體流動的模擬及其數值方法是近年來計算流體力學中的一個研究熱點［1－2］。該問題在流體力學、材料科學、天體力學以及武器物理、慣性約束聚變（ICF）、載人航天與探月工程等前沿科學領域和國家重大工程中有著廣泛而重要的應用背景和實際意義。

多介質流體流動的模擬存在許多困難，其中最主要的困難是如何建立數學模型，以及由該模型所建立的數值方法可能造成速度和壓力在介質界面附近的偽振蕩［1，3－4］。

文獻［2］提出了一個雙密度、雙速度和雙壓力的模型，然而該模型過于復雜難以用于實際計算。人們提出了許多簡化或修正模型［5－7］，但這些模型依然無法消除多介質流體，特別是強激波情況下，速度和壓力在介質界面附近的偽振蕩。本文同樣對BN模型［2］進行簡化和修正，提出了多介質流體模型。

1 數學模型

本文以2種流體為例，提出多介質流體的數學模型，即在整個一維空間x軸方向上流動著2種流體，其形式為：

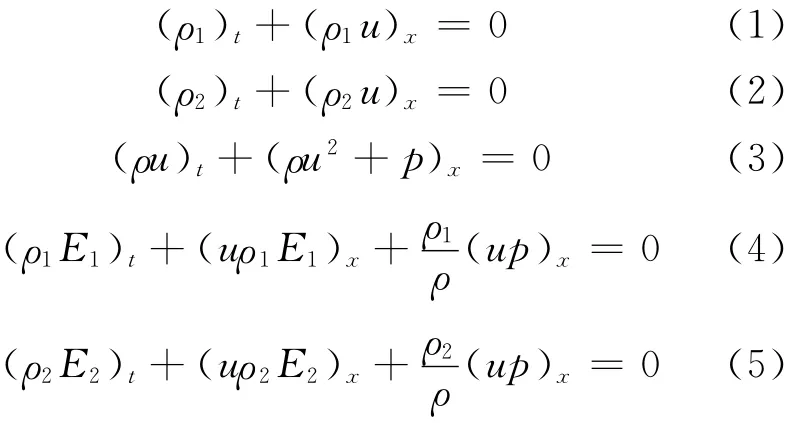
其中，ρ1、ρ2分別表示2種流體的密度；ρ為總密度；u為流體的速度；p為流體的壓力；ρ1E1、ρ2E2分別為2種流體的能量。

此外，本文也采用了組份模型方程來描述物質界面的演化過程，即

其中，0≤α≤1。然而，和BN模型不同的是這里的組份α是用來計算總壓力的，即

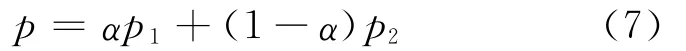
其中，p1、p2分別表示2種流體的壓力，且分別具有狀態方程，即

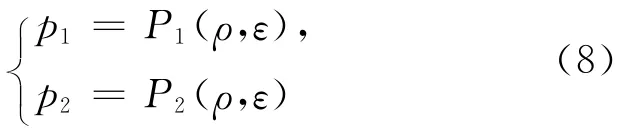
且滿足：

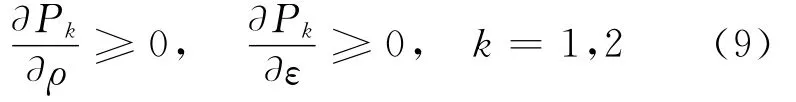
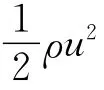
這樣，（1）～（7）式構成了多介質流體流動的數學模型，可以把（1）～（6）式寫成矢量形式，即

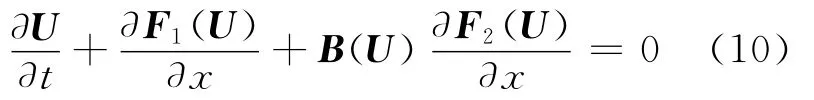
其中

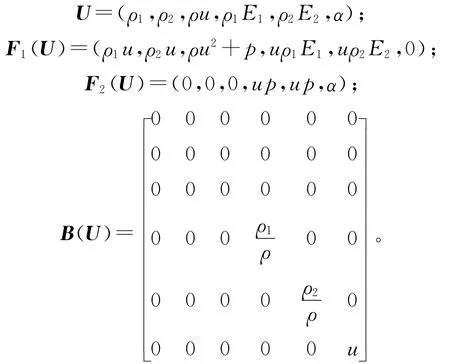
定理1 數學模型（1）～（7）式滿足流體的分質量守恒、總質量守恒、總動量守恒和總能量守恒。

證明 （1）式、（2）式分別表明2種流體的分質量守恒；將（1）式和（2）式相加，可以得到流體總質量守恒；（3）式表明流體的總動量守恒；將（4）式和（5）式相加，可以得到流體總能量守恒。證畢。

定理2 數學模型（1）～（7）式是雙曲型的。

證明 可以將方程組（9）式改寫成非守恒量W＝（ρ1，ρ2，u，p1，p2，α）的擬線性形式，即

很容易得到A（W）的特征值為：

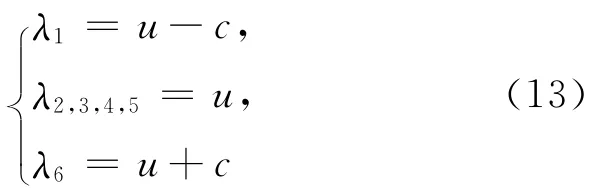
其中（14）式為流體聲速，即

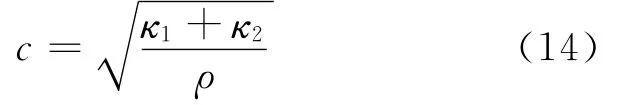
這樣，由ρ1、ρ2、p和α的非負性和（8）式可得c為實數，即數學模型是雙曲型的。

針對多流或多相流的數值模擬中速度和壓力會出現偽振蕩，文獻［9］提出了關于模型及其離散形式有效性的一個準則，即“一個兩相流體，其速度和壓力如果在初始時刻是一致的，那么隨著時間發展，它們依然是一致的”，稱之為UPV（uniform in pressure and velocity）準則；同時指出，產生速度和壓力的偽振蕩的原因，就是這些模型及其數值方法破壞了UPV準則。下文給出的模型能夠消除速度和壓力在介質界面處的偽振蕩的原因，就是模型滿足該準則。

定理3 模型（1）～（7）式滿足UPV準則。

證明 假設一多介質流體的初始速度和壓力分別為常數，u（x，0）≡u0和p（x，0）≡p0。

（1）將（1）式、（2）式代入（3）式，可得：

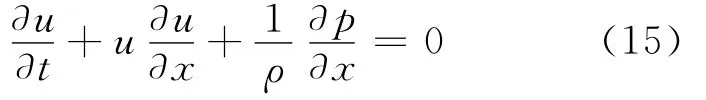
（2）由（11）式可得p1和p2的發展方程，將2個方程相加，可得：

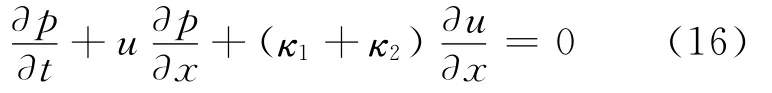
（3）由u和p的初值，可得（15）式、（16）式的唯一解，分別為u（x，t）≡u0和p（x，t）≡p0。證畢。

2 數值方法

采用文獻［4］的方法，給出模型（1）～（6）式二階精度的Lax－Wendroff格式，即

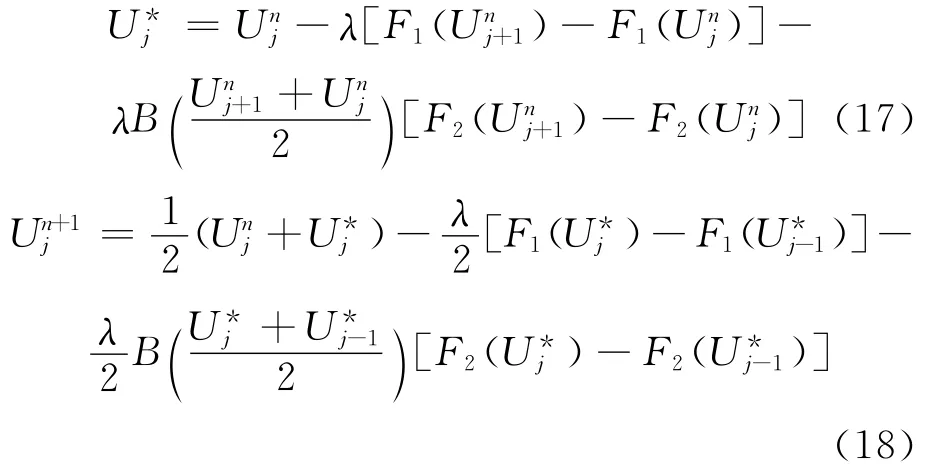
其中，j為空間網格；n為時間網格；λ＝τ／h；h為空間步長；τ為時間步長，并且滿足如下CFL條件：

其中，c為流體聲速。網格上總壓力計算為：

分壓力為：

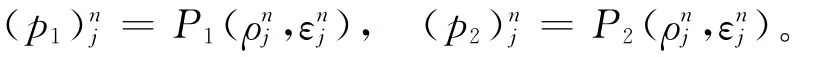
如果將（17）式、（18）式寫成分量形式，并且和定理1的證明類似，則很容易得到如下定理。

定理4 當CFL條件（19）式成立時，（17）式、（18）式滿足分質量守恒、總質量守恒、總動量守恒和總能量守恒。

配電網N-1安全性準則是配電網規劃和運行的重要準則，它規定了在配電網中主變壓器或線路發生故障時，線路或主變壓器所帶負荷可通過與之聯絡的線路進行轉供，即不對外停電。

定理5 （17）式、（18）式滿足 UPV準則。

3 數值算例

通過2個算例來驗證（17）式、（18）式在數值模擬多介質流體流動的有效性，其中實線代表通過求解Riemann問題的精確解，點代表Lax－Wendroff格式的數值解。

算命1 考慮不同理想氣體的激波管問題，初始間斷在x＝0.5位置，初值如下：

當0＜x＜0.5時，ρ1＝1.0，u1＝0，p1＝1.0，γ1＝1.6，α＝1.0；當0.5＜x＜1.0時，ρ2＝0.125，u2＝0，p2＝0.1，γ2＝1.2，α＝0。

本算例選自文獻［1］，這是著名的Sod激波管問題，很多流體力學計算的論文都用它來驗證自己的計算格式，理想氣體的狀態方程為p＝（γ－1）ρε。

算例2 考慮stiff氣體和van der Waals氣體的激波管問題，初始間斷在x＝1位置，初值如下：

當0＜x＜1時，ρ1＝103，u1＝0，p1＝109，γ1＝4.4，π＝6×108，α＝1；當1＜x＜2時，ρ2＝50，u2＝0，p2＝105，γ2＝1.4，a＝5，b＝10－3，α＝0。

圖1 算例1的計算結果

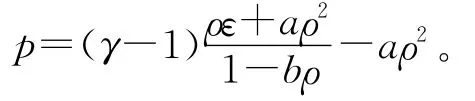
在區間［0，2］上，網格區間數為1 000，時間為0.000 24時的總密度、速度、總壓力和總能量的計算結果［11］，如圖2 所示。

本算例中左邊stiff氣體的π＝6×108，a＝5，b＝10－3，表明是剛性氣體，相當于液體，而且兩邊壓力很大，為強激波。計算結果表明，對于此數值算例，速度和壓力的數值解和精確解也是非常吻合的。

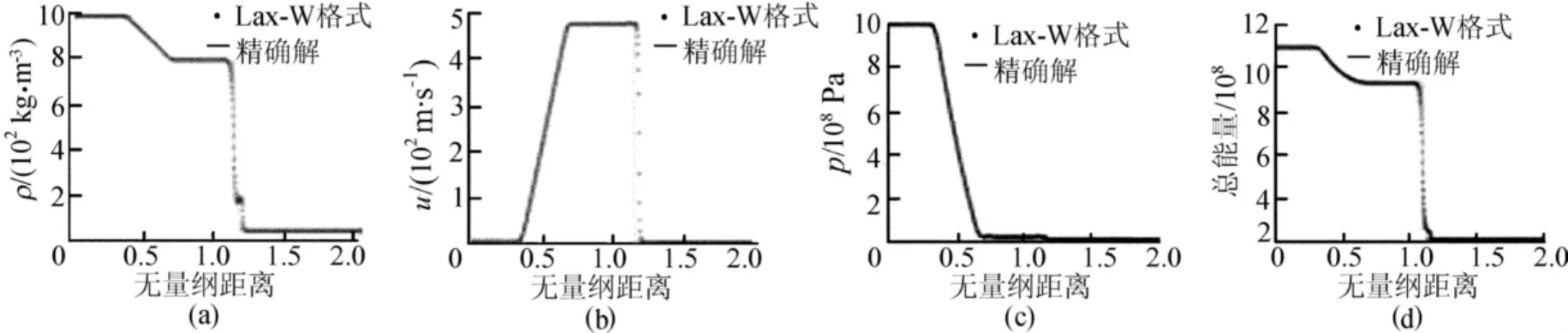
圖2 算例2的計算結果

4 結束語

本文提出了BN模型的一個簡化和修正模型，并采用文獻［4］的方法給出了該模型的具有二階精度的Lax－Wendroff格式，該模型是雙曲型的，而且無論模型和格式都保證了總質量和分質量守恒、總動量和總能量守恒。數值算例表明它有效地模擬可壓縮多介質流體的介質界面的運動，更重要的是它能有效地消除多介質流體，特別是強激波情況下，速度和壓力在介質界面處的偽振蕩。

［1］Abgrall R，Karni S.Computation of compressible multifluid［J］.Journal of Computational Physics，2001，169：594－623.

［2］Baer M R，Nunziato J W.A two－phase mixture theory for the deflagration－to－detonation transition（DDT）in reactive granular materials［J］.International Journal of Multiphase Flow，1986，12：861－889.

［3］Chargy D，Abgrall R，Fezoui L，et al.Comparison of several upwind schemes for multicomponent one－dimensional inviscid flows［R］.INRIA report，1253，1990.

［4］MacCormack R W.The effect of viscosity in hypervelocity impact cratering［J］.Journal of Spacecraft and Rockets，1969，40（5）：757－763.

［5］Allaire G，Clerc S，Kokh S.A five－equation model for the simulation of interfaces between compressible fluids［J］.Journal of Computational Physics，2002，181：577－616.

［6］Berthon C，Nkonga B.Multifluid numerical approximations based on a multipressure formulation［J］.Computers and Fluids，2007，36：467－479.

［7］Saurel P，Petitpas F，Berry R A.Simple and efficient relaxation methods for interfaces separating compressible fluids，cavitating flows and shocks in multiphase mixtures［J］.Journal of Computational Physics，2009，228：1678－1712.

［8］Fedkiw R，Aslam T，Merriman B，et al.A non－oscillatory Eulerian approach to interfaces in multimaterial flows（the Ghost Fluid Method）［J］.Journal of Computational Physics，1999，152：457－492.

［9］Saurel P，Abgrall R.A multiphase Gogunov method for compressible multifluid and multiphase flows［J］.Journal of Computational Physics，1999，150：425－467.

［10］Shyue K M.A fluid－mixture type algorithm for compressible muilticomponent flow with van der Waals equation of state［J］.Journal of Computational Physics，1999，156：43－88.

［11］沃恒洲，姚智華，王國豐，等.發動機噴嘴內部空化流動的數值模擬研究［J］.合肥工業大學學報：自然科學版，2011，34（5）：651－654，670.

A modified Baer－Nunziato model of multifluid flow and its Lax－Wendroff scheme

WU Qiang1，2， M.A.Ullah3
（1.Dept.of Mathematics，Shanghai University，Shanghai 200444，China；2.School of Mathematics，Hefei University of Technology，Hefei 230009，China；3.Dept.of Mathematics，Chittagong University，Chittagong 4331，Banglandesh）

This paper proposes a modified Baer－Nunziato model and its Lax－Wendroff scheme with the second order accuracy for the simulation of material interface of different compressible multifluid flow.Both the model and the scheme fully guarantee the total and individual mass conservation as well as the total momentum and total energy conservation.And the spurious oscillation of velocity and pressure across the material interface is eliminated.Numerical examples verify the effectiveness of the algorithm.

conservation law；multifluid flow；spurious oscillation；Lax－Wendroff scheme

O241.82

A

1003－5060（2012）03－0417－04

10.3969／j.issn.1003－5060.2012.03.029

2011－06－25；

2011－08－12

國家自然科學基金資助項目（10971132）；安徽省自然科學基金資助項目（11040606M06）

吳 強（1973－），男，安徽蕪湖人，上海大學博士生，合肥工業大學講師.

（責任編輯 呂 杰）