基于delta方法泊松分布參數的近似信仰推斷

譚常春， 鄧晴晴， 周 堯

（合肥工業大學 數學學院，安徽 合肥 230009）

基于delta方法泊松分布參數的近似信仰推斷

譚常春， 鄧晴晴， 周 堯

（合肥工業大學 數學學院，安徽 合肥 230009）

文章主要研究了Poisson分布參數λ的近似信仰推斷，利用對數變換后的估計量的漸近正態性對λ建立近似的樞軸方程，并得到其近似信仰分布和置信區間。模擬結果表明，近似信仰區間與Wald置信區間的平均長度幾乎無差異，但近似信仰置信區間覆蓋概率明顯優于Wald置信區間的覆蓋概率。

Poisson分布；delta方法；近似信仰推斷；樞軸方程

泊松分布是最基本的離散分布，不僅在離散數據的分析處理中處于重要的地位，而且在管理科學、運籌學及自然科學等實際問題中有非常廣泛的 應 用［1－3］。 目 前 多 數 利 用 Bayes 方 法［4］、Bootstrap方法［5］研究泊松分布參數的區間估計。

信仰推斷是Fisher在19世紀30年代初期引進的一種構造區間估計的方法。其基本觀點是：設要作θ的區間估計，在抽樣得到樣本（X1，…，Xn）前，對θ一無所知，樣本（X1，…，Xn）透露了θ的一些信息，據此可以對θ取各種值給予不同的“信任程度”，而這可用于對θ作區間估計。這種方法不是基于傳統的概率思想，但對某些困難的統計問題，特別是著名的貝倫斯－Fisher問題，提供了簡單可行的解法。近年來，信仰推斷得到了迅速的發展，特別是利用樞軸方程得到的信仰推斷［6－8］，為小樣本提供了比較精確的推斷結果。但是能夠利用樞軸方法的只有某些具有特定性質的連續性分布，離散分布的信仰分布研究比較少，目前只有二項分布的信仰推斷［9］。

本文利用近似的樞軸方程代替精確的方程，給出了Poisson分布的近似信仰推斷。對λ作對數變換（λ）＝ln（λ＋δ），由變換后函數（λ）的估計量（）的漸近正態性建立關于參數λ的近似樞軸方程，并且導出其近似信仰分布，由此分布構造參數的置信區間。模擬研究表明，該區間比Wald置信區間有更好的小樣本頻率性質。

1 Poisson分布的近似信仰分布及置信區間

設X1，…，Xn為i.i.d樣本，X1～P（λ），其中λ∈（0，＋∞），λ的矩估計和MLE估計＝，由MLE的漸近正態性：并應用Slutsky定理得：

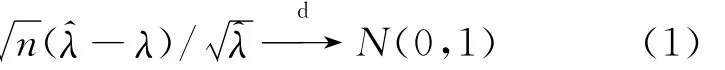
可以得到λ的100（1－α）%Wald置信區間為：

由于正態隨機變量取值在整個實軸上，而λ＞0，通過對λ作一個連續可導變換h（λ），使其取值于整個實數。而且上述Wald置信區間可能出現下限小于0，為避免出現這種情況，令h（λ）＝lnλ，由delta方法可得：

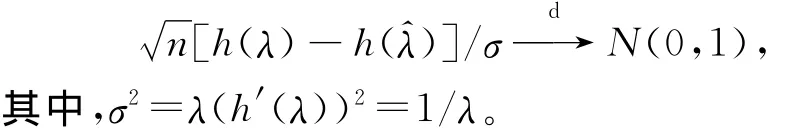
應用Slutsky定理得：

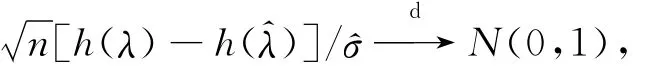
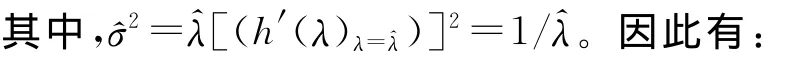
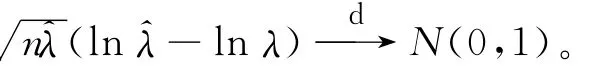
對給定的α，可得：

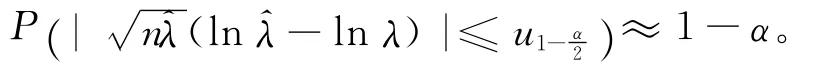
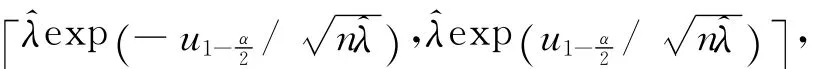
在λ較小時，此置信區間覆蓋概率比較差。考慮到在λ接近0時，此置信區間不理想，對h（λ）進行截尾，令（λ）＝ln（λ＋δ），其中δ＝0.15×，δ的取值參照文獻［9］，而且根據模擬研究，這是一個較好的取法。由delta方法可知：

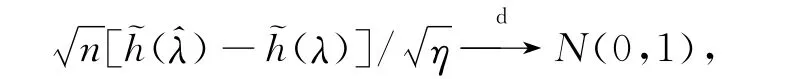
其中，η＝λ／（λ＋δ）2。

同理由Slutsky定理得：

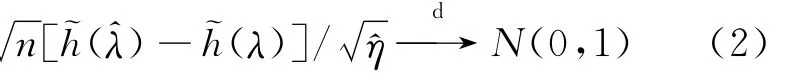
由（2）式可以建立近似樞軸方程，即

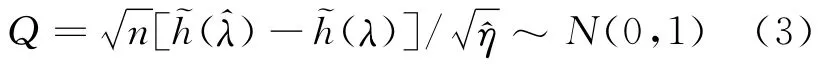
解出λ，可得：

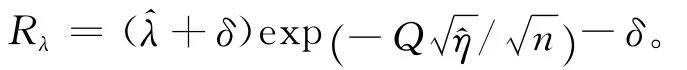
類似區間2的推導過程，可以得到100（1－α）%置信區間為區間3：

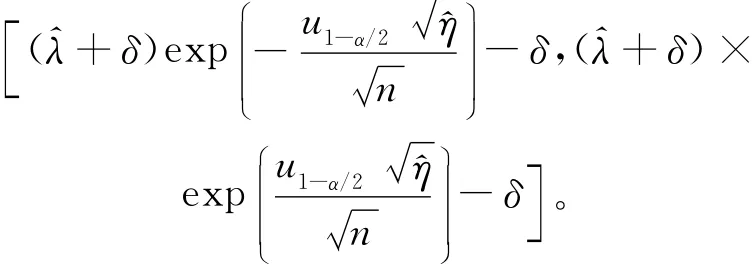
在給定 ｛Xk，k＝1，…，n｝ 后，Rλ的條件分布可以看作λ的一種近似信仰分布，區間3即為該近似信仰分布所對應的等尾置信區間。

2 數據的模擬比較

在本節數據模擬中，取α＝0.05，模擬次數為10 000，n＝30時，截尾前后的近似信仰區間（為方便記，以下均寫為Fiducial置信區間）的覆蓋概率如圖1所示。

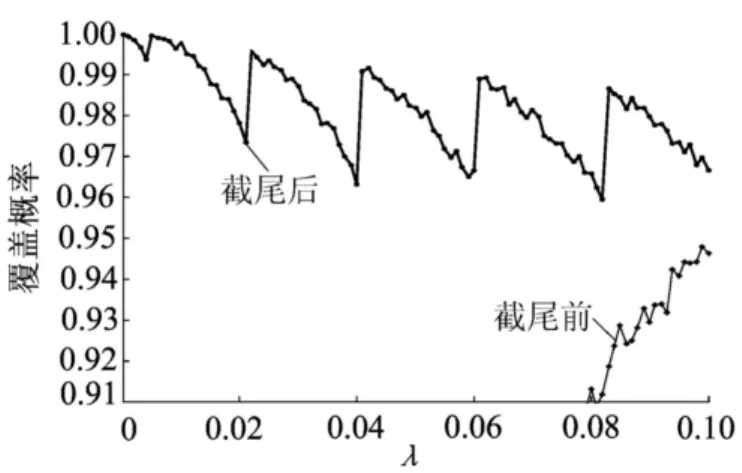
圖1 截尾前后的Fiducial置信區間的覆蓋概率比較

分別在n＝10、15、30、100時，模擬出參數λ的Wald置信區間與Fiducial置信區間的覆蓋概率，模擬結果如圖2所示。

圖2 Wald置信區間與Fiducial置信區間的覆蓋概率比較

由圖2可以得出，對于小樣本（n≤30），Fiducial置信區間的覆蓋概率小于名義水平所對應λ的個數，比Wlad置信區間的覆蓋概率小于名義水平所對應λ的個數少。

對于小樣本，當λ接近0時，Wald區間的覆蓋概率基本上在名義水平之下，而近似信仰區間幾乎都在名義水平之上；當樣本量逐漸增加時，這2種區間的覆蓋概率趨近于名義水平。

由于Fiducial置信區間與Wald置信區間的覆蓋概率在樣本量趨于無窮時都趨于名義水平，因此在小樣本情況下比較兩者的表現。比較的標準是覆蓋概率CP（coverage probability）和平均長度AL（average length）。n＝15時，Fiducial置信區間與Wald置信區間的平均長度的比較如圖3所示。

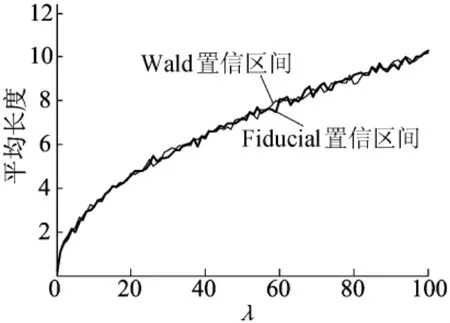
圖3 Fiducial置信區間與Wald置信區間平均長度比較

Fiducial置信區間與Wald置信區間的覆蓋概率和平均長度比較見表1所列。

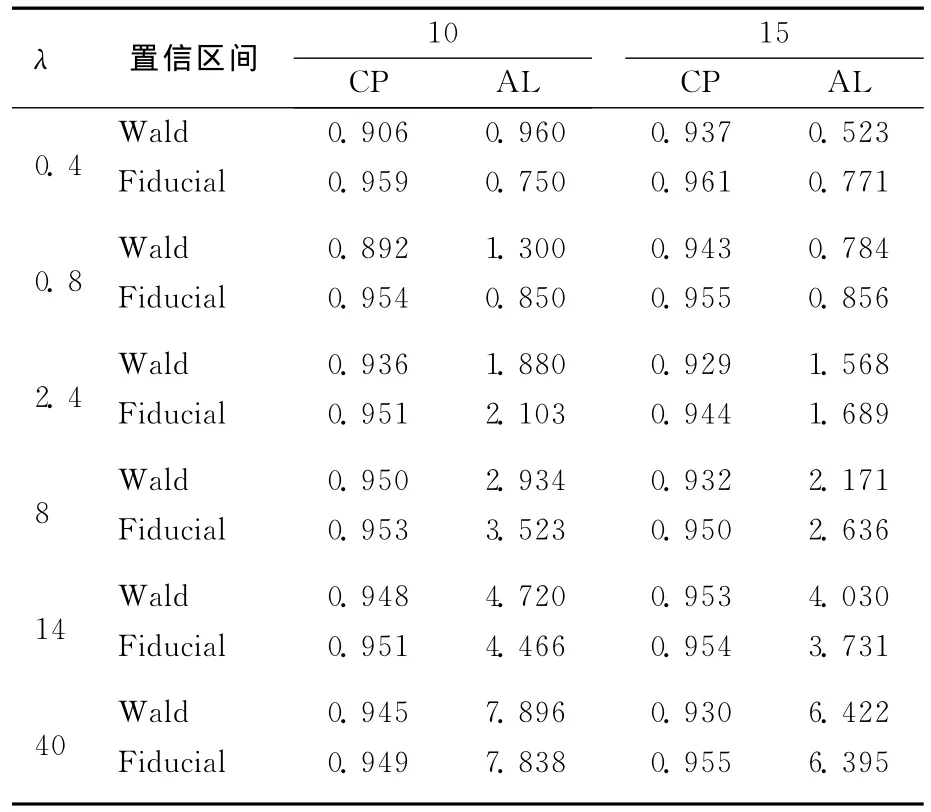
表1 Fiducial置信區間與Wald置信區間比較

由圖3和表1可得，對于小樣本，從整體來看，Fiducial區間長度和 Wald區間長度相差無幾。從局部來看，對于小樣本，雖然Fiducial區間相對Wald區間有一些保守，但是它的覆蓋概率更加可靠。樣本量越大，對每一個固定的λ，其區間長度越小。

3 結束語

本文研究了Poisson分布參數λ的近似信仰區間估計，由λ的對數變換~h（λ）＝ln（λ＋δ）的估計量~h（＾λ）的漸近正態性，結合delta方法構造了λ的近似樞軸方程，導出其近似信仰分布，給出了它的等尾置信區間。模擬分析表明，對于小樣本，利用這種方法構造的區間估計的覆蓋概率明顯高于Wald區間估計的覆蓋概率，而且這2種區間長度幾乎無差異。

［1］何惠珍.商業銀行度量同性質風險總額的計算方法［J］.統計與決策，2008（19）：29－31.

［2］顏亦琪，易建軍，孫華安.泊松分布在水文頻率計算中的應用［J］.人民長江，2010，41（12）：92－94.

［3］黃清泉，洪 沙，吳垣甫.多處理器片上系統數據隊列交易級分析［J］.計算機應用，2008，28（4）：1049－1051，1080.

［4］徐凌云，朱 寧，方愛秋，等.定數截尾情形指數－泊松分布參數的Bayes估計［J］.統計與決策，2010（15）：31－32.

［5］姚源果，夏開萍，羅朝暉.Bootstrap方法下的Poisson分布置信區間的估計［J］.廣西民族大學學報：自然科學版，2008，14（2）：55－57.

［6］Xu Xingzhoug，Li Guoying.Fiducial inference in the pivotal family of distributions［J］.Science in China，2006，49（3）：410－432.

［7］李新民，李國英，徐興忠.限制參數空間上的Fiducial推斷［J］.系統科學與數學，2005，25（6）：729－737.

［8］Wang Min，Zhang Baoxue，Xu Xingzhong.The fiducial inference on the two－parameter exponential distribution［J］.Soochow Journal of Mathematics，2006，32（4）：477－484.

［9］熊世鋒，牟維嫣.二項分布基于logit變換的近似信仰推斷［J］.系統科學與數學，2009，29（8）：1071－1078.

Approximate fiducial inference for the parameter of Poisson distribution based on delta method

TAN Chang－chun， DENG Qing－qing， ZHOU Yao
（School of Mathematics，Hefei University of Technology，Hefei 230009，China）

This paper mainly discusses the approximate fiducial inference of Poisson distribution with the parameterλ.An approximate pivotal equation aboutλis constructed based on the asymptotic normality of a logarithmic－transformed estimator.Then an approximate fiducial distribution and confidence interval of the Poisson parameter are obtained.The simulation results indicate that the average burst length of the approximate fiducial interval and the Wald confidence interval is almost the same，but the coverage probability of the approximate fiducial interval is obviously superior to the Wald confidence interval’s.

Poisson distribution；delta method；approximate fiducial inference；pivotal equation

O212.2

A

1003－5060（2012）03－0421－03

10.3969／j.issn.1003－5060.2012.03.030

2011－05－03；

2011－06－29

教育部重大專項資助項目（309017）；中央高校科研業務費專項資金資助項目（2011HGXJ1078）

譚常春（1977－），男，安徽廬江人，博士，合肥工業大學副教授，碩士生導師.

（責任編輯 閆杏麗）