利率規則與匯率動態調整關系研究

劉曉劍，向 實

（1.湖南大學 金融與統計學院，長沙 410079；2.長沙銀行 金融市場部,長沙 410005）

1 問題的提出

匯率作為開放經濟中的一個基本價格變量，起著調節內外部均衡的重要作用，一個既能反映經濟基本面因素又相對比較穩定的匯率對于一國順利開展對外經濟交往具有十分重要的意義。目前關于匯率動態調整的研究框架主要有兩個：一是Dornbusch(1976)在Mundell-Fleming靜態模型基礎上創立的匯率動態模型框架（簡稱MFD框架），也就是我們熟知的超調模型；二是Obstfeld和Rogoff（1995）在微觀主體跨期最優化決策基礎上建立的動態模型框架（也稱為“新開放經濟宏觀經濟學”，簡稱NOEM框架）。目前無論是MFD還是NOEM研究框架中，絕大多數文獻都是將貨幣政策作為一個外生變量來處理，在這種設定方式下，對貨幣政策與匯率關系的考察事實上僅限于貨幣政策沖擊的范疇，忽略了貨幣政策規則對匯率動態調整可能造成的影響。如果貨幣當局承諾遵守某個確定的貨幣政策規則，這意味著貨幣當局將根據經濟中相關變量的變動情況按照規則對貨幣供給或者利率進行調整。此時貨幣政策已經內生于整個經濟系統，貨幣政策規則中的相關反應系數將改變整個經濟系統的結構參數，同時也改變了系統的動態調整特征。本文在NOEM框架下，通過引入隨機性和Calvo(1983)定價方式，研究貨幣政策規則對匯率動態調整的影響。

2 模型的構建

在NOEM框架下，如果系統存在多個理性預期解，將導致包括匯率在內的整個系統出現不合意的波動。本文旨在研究引入貨幣政策規則之后整個經濟系統理性預期解的性質。對于整個模型需要說明的是：（1）本文引入的貨幣政策規則是利率規則（泰勒規則），假定貨幣當局將根據宏觀經濟變量的變動，按照事先的承諾對短期名義利率進行相應的調整，貨幣政策是內生化的。在引入利率規則之后，對整個經濟的描述就不再需要貨幣需求函數部分，因為如果一國貨幣當局能夠控制利率，必須能夠外生地調整貨幣供給，以保證實際貨幣需求與實際供給相等，這可以大幅度降低我們分析的復雜性。事實上，在一些國家現在使用的大規模經濟模型中甚至已經不再包括貨幣量這個因素，例如美聯儲使用的FSB/US模型（Brayton和Tinsley，1996）。（2）本文模型是對Obstfeld和Rogoff(1995)兩國模型的一種擴展，也采用了在微觀基礎上進行加總的方式。通過恰當地構造加總算子，可以使經濟總量均衡條件的對數線性近似和單個經濟人具有相似的形式。（3）本文模型還引入了隨機性和Calvo(1983)定價方式，Calvo(1983)定價方式的引入意味著即使沒有一個固定的貨幣供給增長率，經濟中仍然可能存在持續的通貨膨脹，同時也意味著經濟中的沖擊不會只持續一期。

2.1 對經濟總需求的設定和推導

假定整個世界由兩個規模相等的國家組成，這兩個國家都是由若干經濟人z構成的閉合集，將世界的總人口正規化為1，世界所有的經濟人分布在一個單位區間[0,1]之內，其中z∈[0,1/2]在本國定居，z∈(1/2,1]在國外定居。每個經濟人既是消費者，又是生產異質性產品的壟斷競爭廠商。在引入隨機性之后，典型經濟人的效用函數形式為：

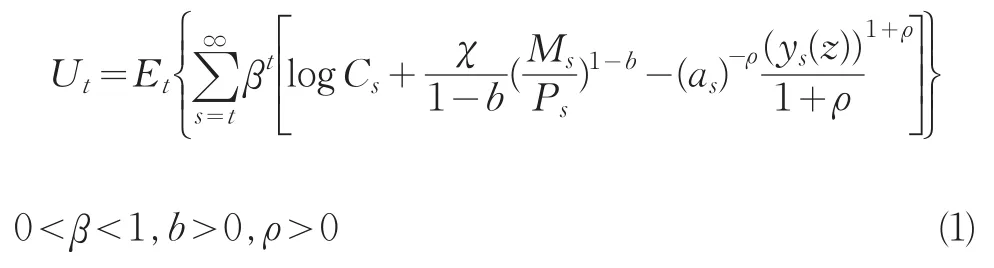
其中E為期望算子，as表示在t期隨機發生的生產力沖擊。β是貼現因子，C為經濟人z的組合消費指數，在此采用了CES形式的定義：

其中η表示各個產品之間的替代彈性，同時也是每個生產者面臨的需求價格彈性，假定η＞1，以保證邊際收入始終為正。

P為消費價格指數（CPI），被定義為

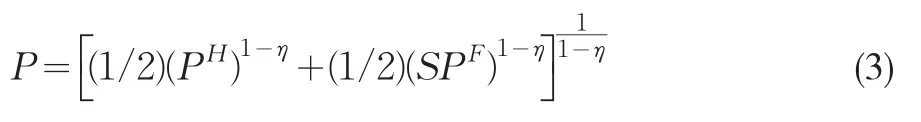
其中PH表示以本國貨幣衡量的國內生產價格指數，PF表示以國外貨幣衡量的國外生產價格指數，相應的可以定義πHt和國內外的生產價格指數通脹率，貿易條件為S為名義匯率（表示為國外貨幣的本國貨幣價格），并且購買力平價成立。此時，對國內外單個商品的需求為：

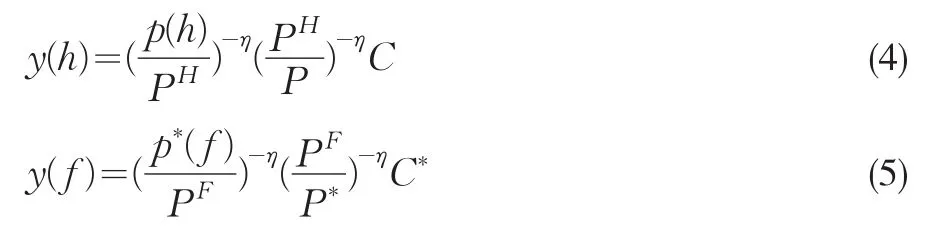
通過構造Dixit-Stiglitz形式的加總算子，對國內和國外商品的總需求為：

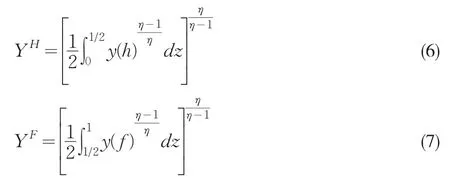
結合(4)到(7)，國內外總需求可表達為：

這幾個條件的對數線性近似形式為：

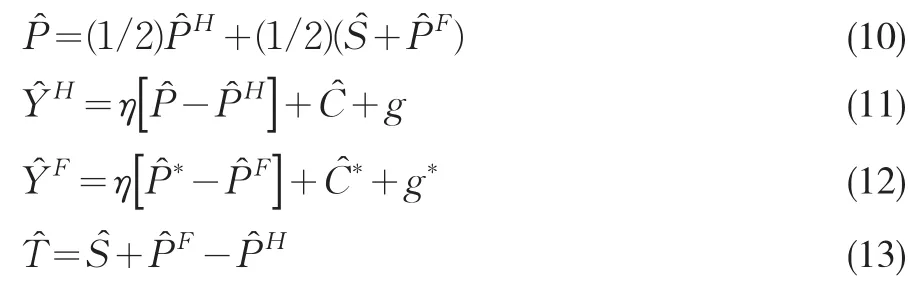
其中g和g*分別表示國內外的總需求沖擊，結合(10)到(13)，國內和國外總需求整理表達為：

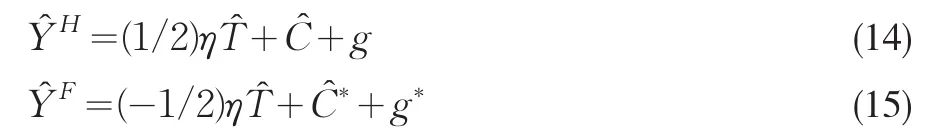
可以看到，盡管每個國家都受到一個共同世界消費的影響，但各個國家的需求沖擊和貿易條件將使得對兩個國家的需求出現差異。由式(14)和式(15)可以有Y?w=C?w+gw，其中gw=(1/2)(g+g*)。在靈活價格下，當經濟中發生各種沖擊時，各個變量會馬上調整到長期穩定狀態，但是在粘性價格下，各個變量的實際值與靈活價格下的長期均衡值會存在缺口，可以定義在粘性價格下世界的產出缺口為

同時，在給定預算約束下求解經濟人的最優化問題，消費歐拉條件的對數線性近似為：

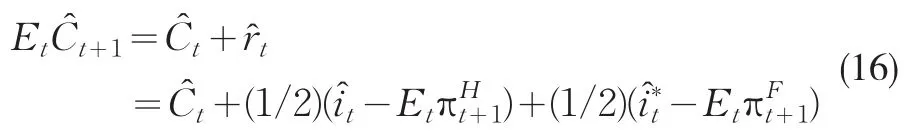
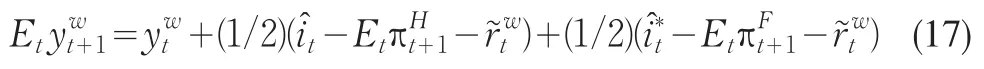
表示在靈活價格時的世界自然真實利率水平。式(15)可以看作是具有微觀基礎的開放經濟中的IS曲線。此外，根據貿易條件的定義，可以有：

2.2 對經濟總供給的設定和推導

經濟中的廠商是壟斷競爭者，對自己的產品具有定價的權力，但同時由于規模不大，單個廠商的定價對整個市場的價格不會產生影響，每個廠商都將整體價格以及消費需求當作給定的變量。在此我們采用Calvo(1983)提出的交錯價格調整模型來刻畫廠商的定價行為。假定廠商不定期地調整價格，并且調整的機會服從泊松分布。在每一期，廠商調整價格的可能性固定為(1-α)，無論距離上一次調整的間隔有多久。在t期廠商有機會調整產品價格時，他也知道到t+k期時仍然有αk的概率繼續維持這一價格，因此理性的廠商在t期會選擇一個價格以使未來預期利潤的現值最大化，即：

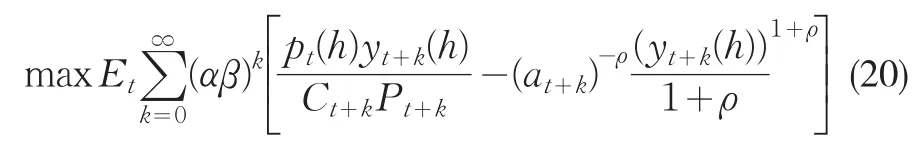
pt(h)為國內廠商t期選擇的價格，yt+k(h)為在給定價格pt(h)的條件下，在t+k期時對產品的需求，可以表示為：

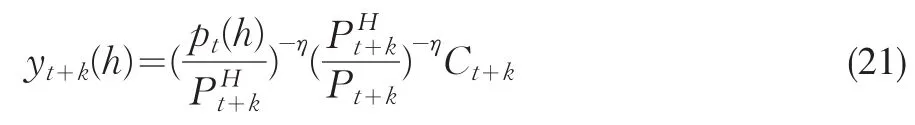
根據一階條件，廠商選擇的最優價格為：

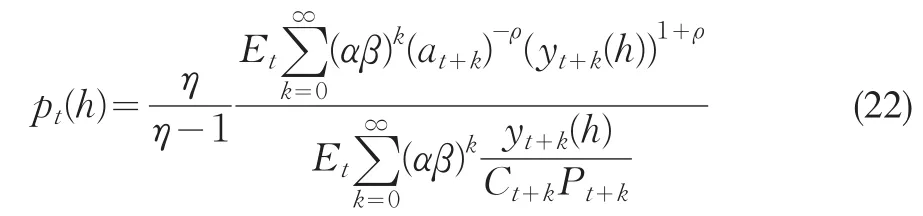
在Calvo定價機制下，國內生產者價格可以下面的狀態方程來表述：

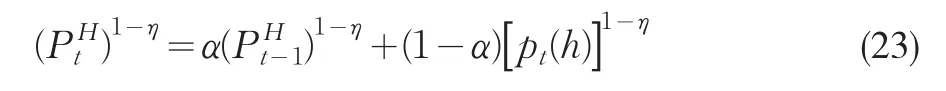
國外廠商也是相同的定價決策方式。根據Benigno和Benigno(2003)①Benigno和Benigno(2003)曾利用這種形式的總供給曲線來分析最優貨幣政策的社會福利效應。，對(4-120)和(4-121)進行對數線性近似，可以得到開放經濟下新凱恩斯主義形式的菲利普斯曲線（NKPC）②對新凱恩斯主義菲利普斯曲線的討論可以參見Gali和Gertler(1999)，Roberts(1998)以及Sbordone(2002)。Gali(2004)曾在一個小國開放經濟模型中得出類似的菲利普斯曲線。：

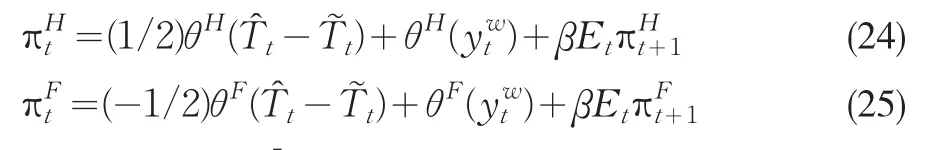
在前面的推導過程中，我們將經濟的總需求和總供給表達為世界產出缺口的形式，目的是將兩個國家放在一個系統中進行討論以簡化分析。同時，還假定兩國具有相同的價格粘性和利率規則反應系數。

2.3 利率規則引入與系統的理性預期解

在一系列對封閉經濟的研究中發現，在引入利率規則之后，有可能導致系統出現多重均衡，即系統的理性預期解是不確定的。而當這種情況發生時就意味著系統中將出現不合意的波動。例如Woodford(1999)的研究表明，當貨幣當局采用泰勒規則時，如果政策目標僅僅是通脹率而不包括產出缺口，為通脹率設置的反應系數必須大于1，系統才會有唯一的和確定的理性預期解，換言之系統才是穩定的，這就是著名的泰勒原則。

在開放經濟框架中，由于包含了更多的變量，使得分析更為復雜。尤其是名義匯率作為一個與外界聯系的經濟變量，不僅是本國的貨幣政策，其他國家的貨幣政策也會對其產生影響，并通過影響相對價格進而對國內的其他經濟變量產生影響。因此，我們在引入貨幣政策規則時，很多時候需要將兩個國家的貨幣政策規則都考慮在內。在此我們將討論三種情形，第一種情形是本國貨幣當局為固定匯率，采取盯住國外利率的利率規則；第二種是兩國都采用泰勒規則；第三種是本國采用泰勒規則，外國的利率規則中還包括了匯率變動率目標。

2.3.1 情形1

我們首先分析一種簡單的利率規則，本國為了維持固定匯率，始終令本國利率等于外國利率，即根據式(19)，由于非抵補利率平價成立，這意味著名義匯率的預期變動率等于0。但是，這并不是一個決定名義匯率均衡的充分條件，考慮一個有界的隨機過程并且當名義匯率變動率遵循的路徑時同樣滿足均衡條件，但此時在名義匯率在t時期取任何值都是均衡值。由于名義匯率的時間路徑是一個隨機游走過程，一些與基本經濟因素無關的外生隨機擾動（即使是平穩的）都將對它的運動產生永久性的沖擊效應，名義匯率將呈現出“太陽黑子”式的運動特征，進而通過相對價格使得經濟中的其他變量產生不合意的波動。

解決這個問題的一種可行方式是，貨幣當局讓本國利率在盯住國外利率的同時，還設置一個名義匯率目標，當名義匯率偏離目標值時，國內利率也會相應的進行調整。即令，其中為名義匯率的目標值。將這個利率規則代入式(19)，并且利用可以得到：

只要σ＞0得到滿足，名義匯率有唯一和確定的理性預期解，在任意時刻t的均衡匯率為

2.3.2 情形2

假定兩國貨幣當局都采用泰勒規則，并且規則反應系數相同，有：

其中?＞0,ψ＞0，將(4-125)代入開放經濟的IS曲線(17)，并對式(24)和式(25)進行合并，利用xw=(1/2)(xH+xF)和兩國具有相同的價格粘性程度，可以得到：

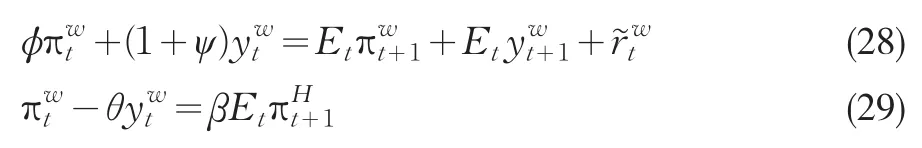
對(28)和(29)繼續進行整理，可以得到：

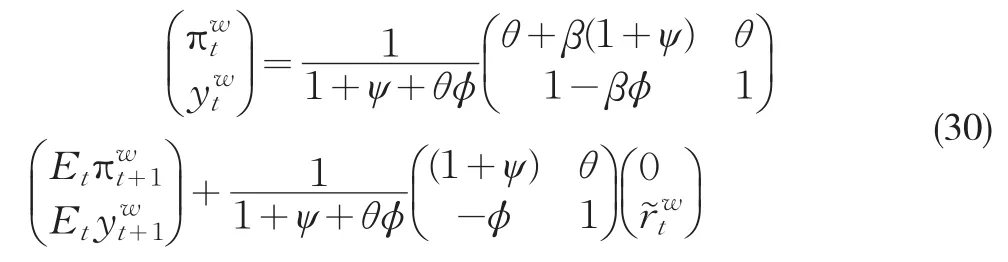
其中等式右邊的第二項對解的性質不構成影響，這一系統有唯一和確定的理性預期解的充分必要條件是，系數矩陣的特征根落在單位圓內。特征根多項式的表達形式為p(λ)=λ2+a1λ+a0，其中：

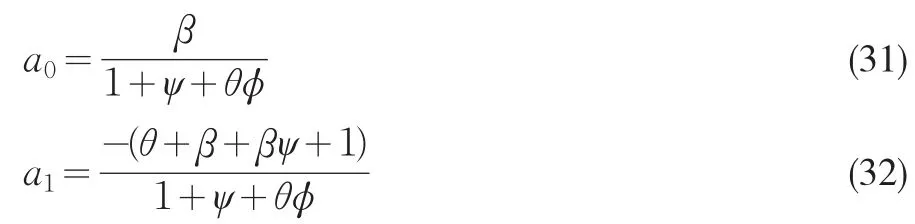
命題1當兩國采用相同的泰勒規則，并且具有相同的價格粘性時，開放經濟系統有唯一和確定的理性預期解的充分必要條件是：

θ(?-1)+(1-β)ψ＞ 0

當泰勒規則中不包括對產出缺口的反應時，就是泰勒規則所要求的條件，對通脹率的反應必須大于1。

2.3.3 情形3

假定本國貨幣當局采用泰勒規則，但國外的利率規則中還包括有匯率變動率目標，可以有：

其中針對產出缺口和通脹率的部分系數相同，?＞0,ψ＞0。將式(33)代入開放經濟的IS曲線(17)，并用式(25)減去式(24)，以及引入式(18)，假定兩國具有相同的價格粘性程度，整理可得：

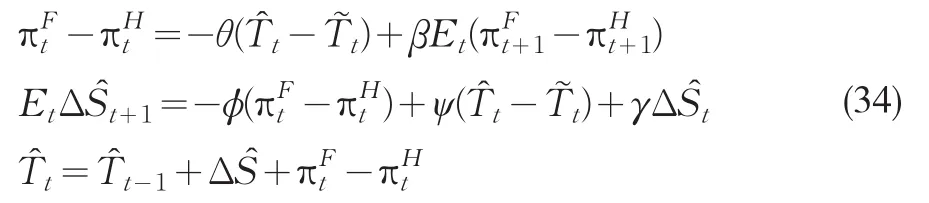
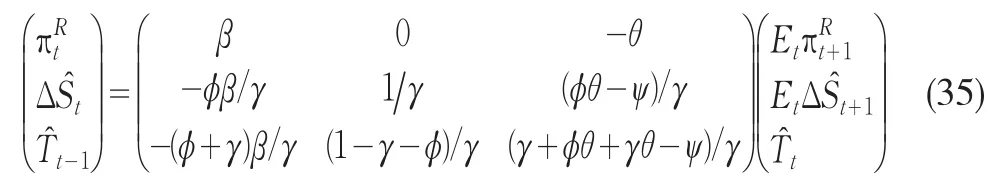
當系數矩陣有兩個特征根落在單位圓內時，系統有唯一和確定的理性預期解，特征根多項式的表達形式為，其中：

當p(1)＞0，p(0)＞0且p(-1)＜0時，系統有兩個根落在單位圓內，這些條件要求θ(?+γ-1)+(1-β)ψ＞0。因此我們可以得到如下命題：

命題2當本國采用泰勒規則，國外的利率規則中除了產出缺口和通脹率目標之外，還包括有匯率變動率目標時。如果兩國具有相同的價格粘性，并且利率規則中對產出缺口和通脹率目標的系數相同，開放經濟系統有唯一和確定的理性預期解的充分必要條件是：

θ(?+γ-1)+(1-β)ψ＞0

此時，如果利率規則中不包括產出缺口，對通脹率目標的反應系數也可以小于1，只要滿足?+γ＞1。

3 結論

本文在新開放經濟宏觀經濟學的研究框架中，探討貨幣政策規則對匯率動態調整的影響。當貨幣當局按照一定的規則實施貨幣政策時，貨幣政策已經內生于整個經濟系統，而不僅僅是以外生變量的角色出現。我們發現，當貨幣政策規則設計不當時，經濟會出現多重均衡，這將導致整個系統出現不合意的波動。同時還證明了在開放經濟中泰勒規則應當滿足的條件，這一條件與封閉經濟中的泰勒原則相同，即當利率規則僅以通脹率為目標時，反應系數必須大于1。并且，貨幣當局無須以名義匯率作為利率規則的目標，以通脹率和產出缺口為目標整個經濟系統就足以實現穩定的要求。當利率規則中包含了名義匯率目標時，系統也存在唯一和確定的理性預期解，但滿足的條件會發生變化，此時要求的是對名義匯率和通脹率的反應系數之和必須大于1。

[1]Benigno,G.,Benigno,P.Price Stability in Open Economies[J].Review of Economic Studies,2003,70(4).

[2]Calvo,G.A.Staggered Prices in a Utility Maximizing Framework[J].Journal of Monetary Economics,1983,(12).

[3]Dornbusch,R.Expectations and Exchange Rate Dynamics[J].Journal of Political Economy,1976，(84).

[4]Faust,J.H.,Rogers.Monetary Policy’s Role in Exchange Rate Behavior[J].Journal of Monetary Economics,2003，(50).

[5]Obstfeld,M.,K.Rogoff.Exchange Rate Dynamics Redux[J].Journal of Political Economy,1995，(103).

[6]Rogoff,R.The Purchasing Power Parity Puzzle[J].Journal of Economic Literature,1996,(34).

[7]Woodford,M..Optimal Monetary Policy Inertia[R].NBER Working Paper,No.7261,Cambridge,MA,1999.

[8]劉波，劉亦文.匯率波動與貨幣代替的實證研究[J].求索，2010，（11）.