平中見奇 凡而不俗——一道高考試題的多樣解答及教學(xué)思考

☉湖北省武漢市黃陂區(qū)第四中學(xué) 李紅春

本題素材平樸、形態(tài)鮮活，可謂一道陳題，但采擷求解過程卻是精彩紛呈，妙趣橫生.

一、問題解決

在課堂上，通過教師的點(diǎn)撥和引導(dǎo)，學(xué)生集思廣益、合作交流、積極探究，動(dòng)態(tài)生成了以下十多種解法.1

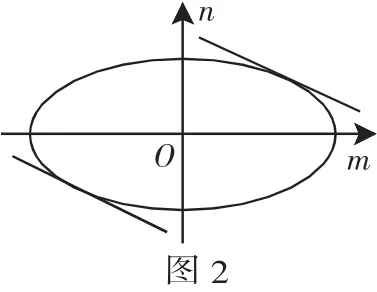
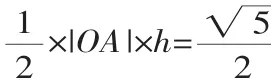
二、解法點(diǎn)評(píng)

解析幾何中的最值問題通常轉(zhuǎn)化為函數(shù)的最值問題加以解決，題目中的變量往往相互聯(lián)系，自變量的選取充滿思辨性.解法1和解法2分別用基本不等式和判別式法求最值是通法，考驗(yàn)學(xué)生的數(shù)學(xué)基礎(chǔ)；解法3和解法6用柯西不等式簡(jiǎn)潔明了，和新課程教學(xué)內(nèi)容掛鉤；解法4和解法5分別通過構(gòu)造“點(diǎn)到直線的距離”和“向量的夾角”模型解題，展現(xiàn)了學(xué)生聯(lián)想和構(gòu)造的能力，是高考考查的熱點(diǎn)；解法7、解法8、解法9滲透了函數(shù)與方程、數(shù)形結(jié)合、等價(jià)轉(zhuǎn)化等思想，充分體現(xiàn)了用數(shù)學(xué)思想引領(lǐng)解題的大趨勢(shì)；解法10、解法11抓住圖形的特點(diǎn)進(jìn)行直觀分析，鍛煉了學(xué)生的直覺思維能力.

三、教學(xué)思考

1.解題教學(xué)應(yīng)以整合知識(shí)、發(fā)散思維和能力為目標(biāo)

數(shù)學(xué)是思維的體操，如今的高考試題常在“知識(shí)網(wǎng)絡(luò)的交匯點(diǎn)、思想方法的交織線和能力層次的交叉區(qū)”內(nèi)命題.本節(jié)課通過一題多解，整合了知識(shí)結(jié)構(gòu)，為學(xué)生從不同角度、不同層次思考問題提供了多維視角，使學(xué)生的思維在靈活性、廣闊性、深刻性、創(chuàng)新性等方面得到了鍛煉，發(fā)展了學(xué)生的思維，提高了學(xué)生的解題能力.眾所周知，學(xué)習(xí)數(shù)學(xué)的過程與數(shù)學(xué)解題緊密聯(lián)系，而數(shù)學(xué)能力的提高在于解題的質(zhì)量而非解題數(shù)量.顯然，分析和研究高考試題的解題思路、探究解題過程是學(xué)生學(xué)會(huì)解題和掌握數(shù)學(xué)技能的有效途徑，對(duì)發(fā)展學(xué)生的思維、提高學(xué)生分析問題和解決問題的能力大有裨益.因而，解題教學(xué)應(yīng)以整合知識(shí)、發(fā)散思維和能力為目標(biāo)，注重引導(dǎo)學(xué)生探究解題的方向和策略，幫助學(xué)生在解題過程中不斷總結(jié)經(jīng)驗(yàn)、積累解題的思維方法，幫助學(xué)生構(gòu)建知識(shí)網(wǎng)絡(luò)，深化學(xué)生的理性認(rèn)識(shí)，提高學(xué)生的思維水平.

2.解題教學(xué)應(yīng)注重挖掘高考題的潛在教學(xué)功能

本題是2006年上海高考文科試題，可謂一道陳題，然而筆者通過挖掘與豐富，這道題便成為學(xué)生課堂發(fā)散性思維訓(xùn)練的良好素材，課堂教學(xué)中既鞏固了高中數(shù)學(xué)中解析幾何、函數(shù)、不等式、三角、向量、導(dǎo)數(shù)等諸多主干知識(shí)，又滲透了函數(shù)與方程、數(shù)形結(jié)合、等價(jià)轉(zhuǎn)化、分類討論等數(shù)學(xué)思想方法的運(yùn)用.我們常常強(qiáng)調(diào)高考題在高三復(fù)習(xí)教學(xué)中的地位和作用，認(rèn)為它是高考命題組集體智慧的結(jié)晶和今后高考命題的生長(zhǎng)點(diǎn)，那么具體怎樣實(shí)施？這是一個(gè)永恒的話題.高考試題通常簡(jiǎn)明扼要、難度適當(dāng)、編排合理，它們?cè)谥R(shí)上具有典型性，在方法上具有示范性.因此，只有教師在平常的教學(xué)中，抓住歷年高考題中的經(jīng)典例子，精心設(shè)計(jì)課堂教學(xué)，注重高考題的分析與研討，在傳授知識(shí)過程中充分挖掘高考題的潛在教學(xué)功能，做到以少勝多，舉一反三，不僅可以鞏固課堂所學(xué)基礎(chǔ)知識(shí)，滲透思想方法和數(shù)學(xué)思維，還能激發(fā)學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣，開拓學(xué)生的解題思路，擴(kuò)大解題的“武器庫(kù)”，這樣才能有效地培養(yǎng)學(xué)生的數(shù)學(xué)能力，真正為學(xué)生減負(fù).