淺析圓錐曲線中的配方法、待定系數法、換元法解題技巧
☉江蘇省蘇州大學附屬中學 陸菊芳
解析幾何內容是歷年來高考數學試題中能夠拉開成績差距的內容之一,該部分試題往往有一定的難度和區分度,所以掌握好其中的解題方法會起到事倍功半的效果.
一、配方法、待定系數法、換元法簡介
配方法、待定系數法、換元法是三種常用的數學基本方法.這些方法是數學思想的具體體現,是解決問題的手段,它不僅有明確的內涵,而且具有可操作性,有實施的步驟和作法.
二、例題解析
(1)配方法:配方法是對數學式子進行一種定向的變形技巧,由于這種配成“完全平方”的恒等變形,使問題的結構發生了轉化,從中可找到已知與未知之間的聯系,促成問題的解決.
例1 已知如圖1所示,F1和F2為雙曲線的兩個焦點,點P在雙曲線上且滿足∠F1PF2=90°,則△F1PF2的面積是_________.
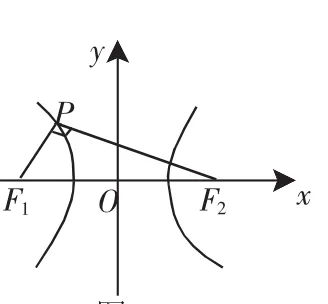
圖1

評注:配方法實現了“平方和”與“和的平方”的相互轉化.
(2)待定系數法:待定系數法的實質是方程的思想,這個方法是將待定的未知數與已知數統一在方程關系中,從而通過解方程(或方程組)求得未知數.
例2 設雙曲線的中心是坐標原點,準線平行于x軸,離心率為,已知點P(0,5)到該雙曲線上的點的最近距離是2,求雙曲線方程.
二次曲線的對稱軸為y=4,而函數的定義域為y≥a或y≤-a,因此,需對a≤4與a>4分類討論.
(1)當a≤4時,如圖2可知函數在y=4處取得最小值.
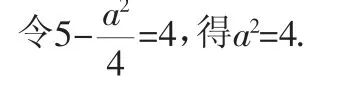
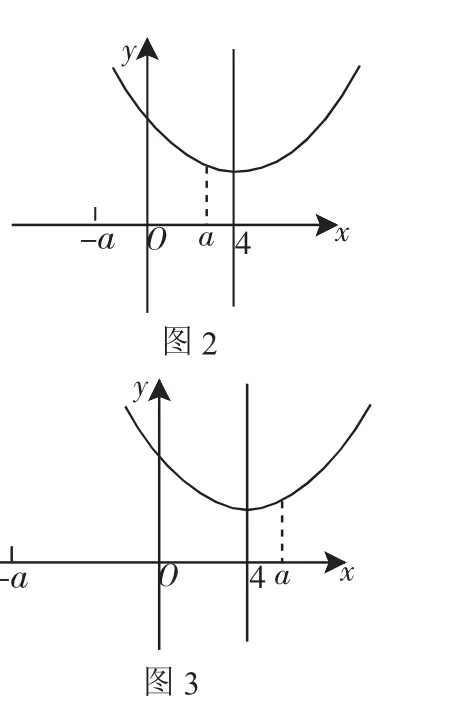
(2)當a>4時,如圖3可知函數在y=a處取得最小值.

評注:此題是利用待定系數法求解雙曲線方程的,其中利用配方法求解二次函數的最值問題,由于二次函數的定義域與參數a有關,因此需對字母a的取值分類討論,從而得到兩個解,同學們在解答學習題時應學會綜合運用數學思想方法解題.
(3)換元法:換元法是一種變量代換,它是用一種變數形式去取代另一種變數形式,從而使問題得到簡化,換元的實質是轉化.
例3 如圖4,已知在矩形ABCD中,C(4,4),點A在曲線x2+y2=9(x>0,y>0)上移動,且AB,BC兩邊始終分別平行于x軸,y軸,求使矩形ABCD的面積最小時點A的坐標.
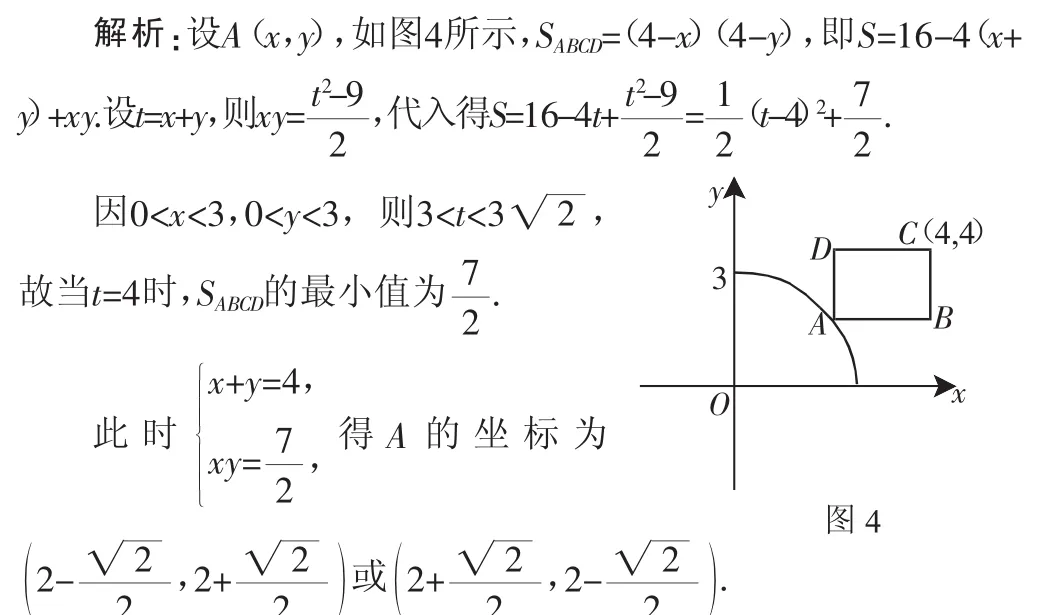
評注:換元前后新舊變量的取值范圍是不同的,這樣才能防止出現不必要的錯誤.
故對于高考,從命題所追求的目標來看,小題所涉及的內容一定會注意到知識的覆蓋,兼顧到對能力的要求.所以最近幾年高考命題的熱點有:
(1)與其他知識進行綜合,在知識網絡的交匯處設計試題(如與向量綜合,與數列綜合,與函數、導數及不等式綜合等);
(2)直線與圓錐曲線的位置關系,由于該部分內容體現解析幾何的基本思想方法——用代數的手段研究幾何問題,因此該部分內容一直是考試的熱點;
(3)求軌跡方程;
(4)應用題.
因此需要同學們總結和掌握解題方法和技巧,解題時手到擒來.

