高中數(shù)學(xué)概念教學(xué)『三部曲』

☉江蘇省啟東市呂四中學(xué) 許紅衛(wèi)

高中數(shù)學(xué)概念教學(xué)『三部曲』

☉江蘇省啟東市呂四中學(xué) 許紅衛(wèi)

新課標(biāo)強(qiáng)調(diào)學(xué)生是教學(xué)的主體，倡導(dǎo)體驗(yàn)式和探究式教學(xué)，因此，數(shù)學(xué)概念的教學(xué)過(guò)程應(yīng)注重學(xué)生的本位性，重視學(xué)生在概念學(xué)習(xí)中從感性到理性的過(guò)程體驗(yàn)，在體驗(yàn)中學(xué)習(xí)概念，深化對(duì)概念內(nèi)涵、外延的理解，提升學(xué)生概念的內(nèi)化程度．那么按照新課程的理念，高中數(shù)學(xué)概念教學(xué)應(yīng)當(dāng)如何施展呢？筆者認(rèn)為概念教學(xué)應(yīng)踏好節(jié)奏，下面結(jié)合教學(xué)實(shí)例淺談幾點(diǎn)做法．

一、“課堂啟動(dòng)”——概念教學(xué)問(wèn)題化

數(shù)學(xué)概念是構(gòu)成高中數(shù)學(xué)知識(shí)大廈的基石，學(xué)生概念理解上的缺失勢(shì)必導(dǎo)致數(shù)學(xué)思想方法和解決實(shí)際問(wèn)題的貧瘠化，傳統(tǒng)教學(xué)模式中直接灌輸?shù)亩啵瑢W(xué)生還沒(méi)有準(zhǔn)備好，還沒(méi)有能夠進(jìn)入思考狀態(tài)，教師就將枯燥的符號(hào)和公式呈現(xiàn)在學(xué)生的面前，導(dǎo)致學(xué)生學(xué)習(xí)興趣的低落，更談不上探究欲望的激發(fā)．理論分析和實(shí)踐經(jīng)驗(yàn)表明，課堂需要一個(gè)啟動(dòng)的過(guò)程，即需要在課堂伊始從學(xué)生的最近發(fā)展區(qū)出發(fā)創(chuàng)設(shè)教學(xué)情境，課堂啟動(dòng)的過(guò)程是引起學(xué)生注意、促使其融入情境的過(guò)程，筆者在教學(xué)實(shí)踐中注重以問(wèn)題為中心，概念教學(xué)問(wèn)題化，將教學(xué)目標(biāo)分解為幾個(gè)具體任務(wù)來(lái)驅(qū)動(dòng)整個(gè)概念的教學(xué)．

例如，“直線與圓的位置關(guān)系”這一概念的導(dǎo)入，筆者從學(xué)生的原有認(rèn)知基礎(chǔ)出發(fā)，設(shè)置如下幾個(gè)問(wèn)題：

（1）從原有的概念中回憶一下，兩條直線存在著哪些位置關(guān)系?

（2）兩條直線的位置關(guān)系可以用哪些方程來(lái)表示?

（3）試想一下，直線與圓存在哪幾種位置關(guān)系?

（4）如何對(duì)直線與圓之間的位置關(guān)系進(jìn)行判定？你能想到什么方法?

在問(wèn)題情境的創(chuàng)設(shè)上，在對(duì)上述幾個(gè)問(wèn)題的處理上，筆者借助多媒體將直線與圓的位置關(guān)系的一些圖形進(jìn)行了動(dòng)態(tài)演示，最大限度地提高學(xué)生的感性認(rèn)識(shí)，引導(dǎo)學(xué)生的思維向著更為廣闊的方向發(fā)展．

再例如，“映射與函數(shù)”這一概念的導(dǎo)入，筆者從現(xiàn)實(shí)生活中取景進(jìn)行情境的創(chuàng)設(shè)：汽車進(jìn)入了千家萬(wàn)戶，一個(gè)實(shí)際的問(wèn)題自然生成“現(xiàn)在車管所在對(duì)車輛管理上，如何做能夠確保管理的有效性？”

筆者在提出這個(gè)實(shí)際問(wèn)題后，學(xué)生的興趣和注意力立刻被轉(zhuǎn)移過(guò)來(lái)了，答案亦是學(xué)生熟知的，即給每一輛車配個(gè)“身份證”，即“上牌照”，不同的汽車有一個(gè)不同的號(hào)碼與之對(duì)應(yīng)！接著由此類推，設(shè)置幾個(gè)與“映射”概念相關(guān)的小問(wèn)題，通過(guò)對(duì)問(wèn)題的回答讓學(xué)生獲得一定的感性認(rèn)識(shí)，學(xué)生對(duì)概念的第一印象就尤為深刻，有利于其在接下來(lái)的探究過(guò)程中學(xué)習(xí)能動(dòng)性的充分釋放.

二、“課堂加速”——概念形成過(guò)程化

概念學(xué)習(xí)的過(guò)程是一個(gè)從未知到已知的探究過(guò)程，在具體學(xué)習(xí)中應(yīng)從學(xué)生的最近發(fā)展區(qū)出發(fā)，結(jié)合知識(shí)的特點(diǎn)，加強(qiáng)直觀教學(xué)，由具體到抽象，適當(dāng)?shù)亍凹铀佟保凹?jí)而上，通過(guò)教師情境的設(shè)置和問(wèn)題的牽引，讓學(xué)生從感性到理性體驗(yàn)概念構(gòu)建的過(guò)程.

圖1

圖2

例如，“函數(shù)的奇偶性”一節(jié)概念課教學(xué)中，筆者首先借助多媒體投影了如圖1、圖2所示的兩個(gè)函數(shù)圖像.引導(dǎo)學(xué)生對(duì)圖像進(jìn)行觀察，自己去發(fā)現(xiàn)圖中兩個(gè)函數(shù)的特征（圖1關(guān)于y軸對(duì)稱，圖2關(guān)于坐標(biāo)原點(diǎn)對(duì)稱），在此發(fā)現(xiàn)的基礎(chǔ)上，筆者投影出問(wèn)題：

結(jié)合兩幅圖形，看看f（－1）與f（1）、f（－2）與f（2）、f（－3）與f（3）…存在著怎樣的關(guān)系，并歸納出兩個(gè)函數(shù)在代數(shù)形式上的特征（圖1可表示為f（－x）=f（x）；圖2可表示為f（－x）=－f（x）），完成從圖像表征向符號(hào)表征的轉(zhuǎn)化，對(duì)這兩類函數(shù)進(jìn)行定義和區(qū)分的需求自然生成，此時(shí)筆者引導(dǎo)學(xué)生自己看書(shū)理解和提煉偶函數(shù)和奇函數(shù)的定義，再結(jié)合圖形實(shí)現(xiàn)概念的自主學(xué)習(xí)，同時(shí)了解了其特征：

（1）偶函數(shù)的圖像關(guān)于y軸對(duì)稱；奇函數(shù)的圖像關(guān)于坐標(biāo)原點(diǎn)對(duì)稱.（2）奇偶函數(shù)的定義域一定關(guān)于原點(diǎn)對(duì)稱.

對(duì)概念有了一定的了解，筆者將例題分為兩組引導(dǎo)學(xué)生對(duì)函數(shù)的奇偶性進(jìn)行辨析.

學(xué)生借助題組1的解決，對(duì)奇偶性定義進(jìn)行加深理解，并初步涉及判定方法，筆者結(jié)合學(xué)生具體的解答實(shí)際，予以方法上的規(guī)范.在掌握方法的基礎(chǔ)上，筆者進(jìn)一步加大難度進(jìn)行探究.

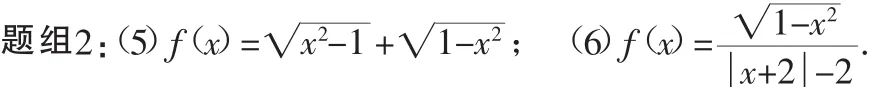
學(xué)生借助題組2這兩道提高題的探究，在定義及判定方法上進(jìn)一步加深理解，同時(shí)領(lǐng)會(huì)定義域的重要性.

在經(jīng)歷了兩個(gè)題組的思考后，函數(shù)的奇偶性分類也自然形成，存在以下四個(gè)類型：偶函數(shù)、奇函數(shù)、既奇又偶函數(shù)和非奇非偶函數(shù).

三、“課堂反饋”——概念應(yīng)用自主化

數(shù)學(xué)概念具有系統(tǒng)性，在某一節(jié)概念課的教學(xué)中，學(xué)生認(rèn)識(shí)和形成概念后，概念還是孤立的，未能融入整個(gè)知識(shí)體系中，記憶難以穩(wěn)固，為此，要徹底地理解和掌握概念并內(nèi)化為學(xué)生的能力，需要通過(guò)一定的小型綜合題來(lái)應(yīng)用概念.

以上述的“函數(shù)的奇偶性”一節(jié)課教學(xué)為例，筆者在最后設(shè)置了2道小型的綜合題，引導(dǎo)學(xué)生在前后知識(shí)背景下，自主應(yīng)用概念，并反饋所學(xué).

反饋題1：奇函數(shù)f（x）在（0，+∞）上為減函數(shù)，求證：f（x）在（－∞，0）上為減函數(shù).

反饋題2：已知一偶函數(shù)，在x＞0時(shí)表達(dá)式為f（x）=x2+3x，試求在x＜0時(shí)的表達(dá)式.

反饋題的設(shè)置，不應(yīng)該是課本例題或是知識(shí)點(diǎn)的簡(jiǎn)單重復(fù)，應(yīng)該從知識(shí)的學(xué)習(xí)過(guò)程體驗(yàn)出發(fā)，既要避免簡(jiǎn)單練習(xí)引起的乏味感，也要避免復(fù)雜練習(xí)引起的挫敗感，基于本課所學(xué)知識(shí)適當(dāng)?shù)嘏c前期所學(xué)知識(shí)有機(jī)組合，通過(guò)多元化的拓展，讓學(xué)生在自主應(yīng)用過(guò)程中內(nèi)化所學(xué)知識(shí)，同時(shí)在對(duì)原有概念思考的過(guò)程中獲得新的感悟.當(dāng)然，考慮到學(xué)生的個(gè)體差異，不可能所有的學(xué)生在應(yīng)用數(shù)學(xué)概念解決問(wèn)題時(shí)，都能快速地得到正確的結(jié)果，出現(xiàn)漏洞是正常現(xiàn)象，是其思維最為真實(shí)的反映，恰好可以借助做題的過(guò)程將概念理解上的偏差暴露出來(lái)，及時(shí)地發(fā)現(xiàn)理解上的缺陷，及時(shí)地予以彌補(bǔ)，有利于概念體系更好、更穩(wěn)定的構(gòu)建.甚至有些時(shí)候，強(qiáng)化學(xué)生的思維縝密性，還需要設(shè)置一些“陷阱題”，“挖坑”讓學(xué)生先摔疼了，再?gòu)钠溴e(cuò)誤出發(fā)，順勢(shì)進(jìn)行成因的剖析，引導(dǎo)學(xué)生體驗(yàn)“從跌倒到爬起”的過(guò)程，更為全面的理解概念和方法.

總之，高中數(shù)學(xué)教學(xué)中最為重要的一環(huán)為概念教學(xué)，概念是整個(gè)高中數(shù)學(xué)體系的樞紐，概念教學(xué)難也是不爭(zhēng)的事實(shí)，傳統(tǒng)的教學(xué)模式下學(xué)生很快地能夠記住概念，不過(guò)對(duì)概念的理解難以深入，由于學(xué)習(xí)缺乏自主性，某一個(gè)概念學(xué)習(xí)的經(jīng)驗(yàn)很難遷移應(yīng)用到其他數(shù)學(xué)概念的學(xué)習(xí)中去，導(dǎo)致概念學(xué)習(xí)連貫性的缺失，鏈?zhǔn)椒磻?yīng)下，學(xué)生的數(shù)學(xué)素養(yǎng)和解決數(shù)學(xué)問(wèn)題的能力得不到很好的提升，所以，我們從新課程本身教學(xué)的理念出發(fā)，注重學(xué)生課堂學(xué)習(xí)的參與度，通過(guò)學(xué)生的自主探究，吸取概念中的“營(yíng)養(yǎng)”，提升數(shù)學(xué)素養(yǎng).

1.李啟柱.數(shù)學(xué)建構(gòu)主義學(xué)習(xí)及主要特征［J］.數(shù)學(xué)通訊，2000（5）：10.

2.郭桂華，劉新春.培養(yǎng)數(shù)學(xué)能力的三個(gè)重要環(huán)節(jié)［J］.中學(xué)數(shù)學(xué)月刊，2008（2）.