利用三次函數圖像 破解高考導數試題

☉湖北省襄陽市第五中學 謝 偉

☉湖北省襄陽市第四中學高中部 王 丹

利用三次函數圖像 破解高考導數試題

☉湖北省襄陽市第五中學 謝 偉

☉湖北省襄陽市第四中學高中部 王 丹

與三次函數有關的問題是歷年高考命題的熱點，三次函數的圖像是三次函數性質的直觀反映，借助函數圖像，可以直觀地研究對應函數的性質.本文以近年與三次函數有關的高考試題為例，分析如何結合三次函數的圖像解決這類問題．

一、求解單調區間和極值點的問題

例1（2012年重慶文17）已知函數f（x）=ax3+bx+c在x=2處取得極值為c－16．

（1）求a、b的值.

（2）若f（x）有極大值28，求f（x）在［-3，3］上的最小值．

解析：（1）a=1，b=－12（過程略）；

（2）f′（x）=3x2－12．令f′（x）=0，得x=±2．當x∈（－3，－2）∪（2，3）時，f′（x）＞0，當x∈（－2，2）時，f′（x）＜0，f（x）在（－3，－2）和（2，3）上遞增；f（x）在（－2，2）上遞減．結合圖1知，f（x）在［-3，3］上的最大值是f（－2）和f（3）中的較大者，即最大值為f（－2）=c+16=28，即c=12．由于f（x）在［-3，3］上的最小值是f（-3）和f（2）中的較小者，因此，最小值為f（2）=－4．

評注：本題利用三次函數的圖像，直觀揭示了函數在區間內的單調性與極值，并能夠便捷地確定函數f（x）在［－3，3］內的最大值和最小值．這樣能夠快速解題，避免出錯．

圖1

二、分析兩個函數交點個數的問題

例2 （2012年全國理10）已知函數y=x3－3x+c的圖像與x軸恰有兩個公共點，則c＝（ ）.

A.－2或2 B.－9或3

C.－1或1 D.－3或1

解析：依題設，方程x3－3x=－c有兩個不等實根．設f（x）=x3－3x，則f′（x）=3x2－3，令f′（x）=0，得x=±1.當x∈（－∞，－1）∪（1，+∞）時，f′（x）＞0；當x∈（－1，1）時，f′（x）＜0.即f（x）在（－∞，－1）和（1，+∞）上遞增，在（－1，1）上遞減，極大值是f（－1）=2，極小值是f（1）=－2．結合圖2可知，若f（x）=x3－3x和y=－c的有兩個交點，則c=±2時．選A．

圖2

評注：本題轉化為求解函數f（x）=x3－3x和y=－c的圖像有兩個交點時c的值．觀察圖像可知，y=－c經過曲線的極值點時，兩個函數圖像有兩個交點．利用圖像解題思路清晰，容易理解.

三、解決含參數函數的討論的問題

例3（2012年北京理18）已知函數f（x）=ax2+1（a＞0），g（x）=x3+bx.

（1）若曲線y=f（x）與曲線y=g（x）在它們的交點（1，c）處具有公共切線，求a、b的值.

（2）當a2=4b時，求函數f（x）+g（x）的單調區間，并求其在區間（－∞，－1］上的最大值．

解析：（1）a=3，b=3（過程略）.

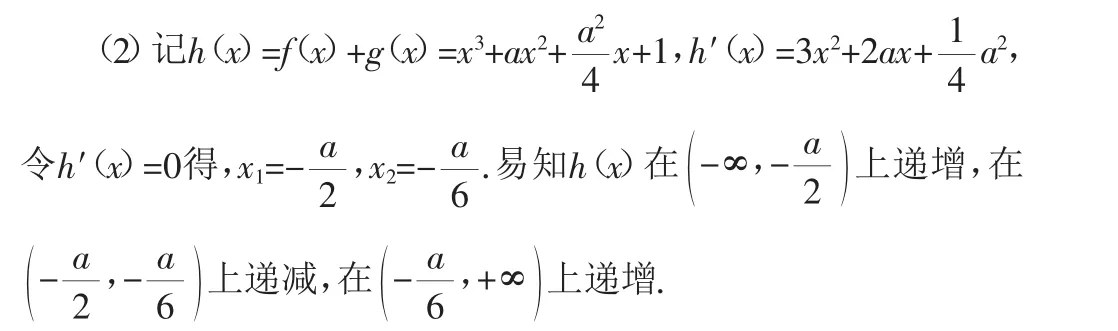
圖3-1

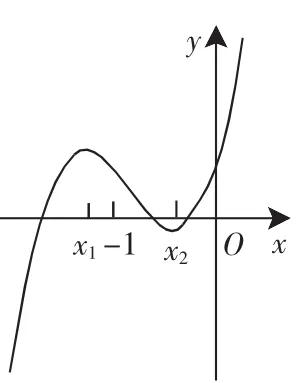
圖3-2

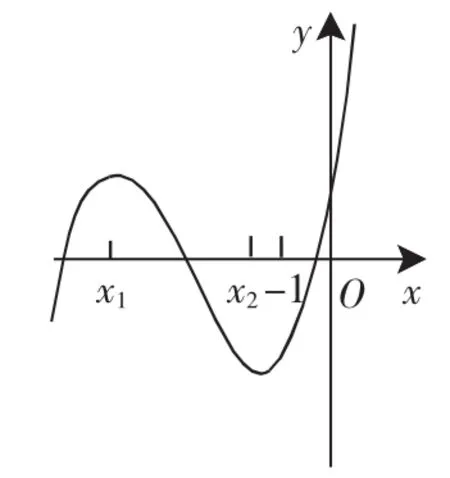
圖3-3

評注：本題結合圖像可知，按照－1與x1和x2之間的大小關系分3類討論，結合圖像有助于便捷地找到分類討論的標準，使得分類清楚、條理清晰，為解決問題提供了方便．

四、研究與導數有關的其他問題

例4 （2010年天津文20）已知函數f（x）=ax3－1.5x2+1（x∈R），其中a＞0．

（1）若a=1，求曲線f（x）在（2，f（2））處的切線方程.

（2）若在區間［－0.5，0.5］上，f（x）＞0恒成立，求a的取值范圍．

解析：（1）y=6x－9.

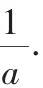
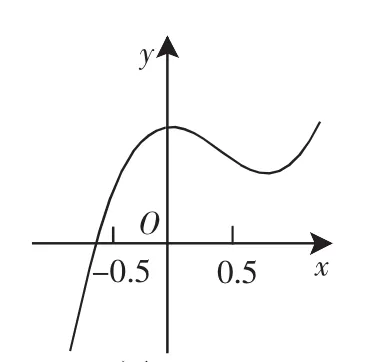
圖 4－1

圖 4－2

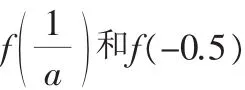
高考導數試題除了考查三次函數的相關問題以外，還考查運用導數解決其他函數的有關問題，我們同樣可以利用函數圖像便捷地解決這類問題．

解析：（1）f′（x）=x（4x2－10x+4）．令f′（x）=0，得x1=0，x2=0.5，x3=2．當x∈（－∞，0）∪（0.5，2）時，f′（x）＜0；當x∈（0，0.5）∪（2，+∞）時，f′（x）＞0，如圖5中C1.f（x）在（0，0.5）和（2，+∞）上遞增，在（－∞，0）和（0.5，2）上遞減．

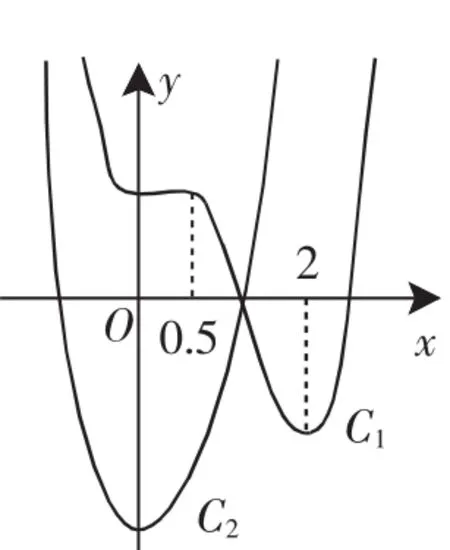
圖5

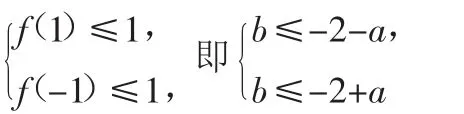
評注：本題涉及四次函數的單調性和最值，在四次函數的導函數對應的方程有三個不同實根的條件下，若四次項系數大于0，則圖像呈單峰雙谷的W型；若四次項系數小于0，則圖像呈雙峰單谷的M型．當導函數對應方程的根的情況變化時，單調性、極值和最值會隨之變化．

如果我們能夠熟練掌握三次函數的圖像，充分運用數形結合的數學思想，就能夠準確快速地解題，破解相關導數試題．同時也能夠用類似的方法研究其他函數的的相關問題．