方程搭臺 函數“唱戲”

☉江蘇省沭陽如東中學 高安軍

函數和方程有著千絲萬縷的聯系，在近年的高考中，頻頻出現一些方程和函數結合起來的題目，在解答時，主要是利用函數的特性來解，下面舉例說明.

A.4 B.5 C.7 D.8

解析：方程f2（x）+bf（x）=0可化為f（x）=0或f（x）=-b.而y=f（x）的圖像大致如圖所示.

由圖可知，直線y=0（即x軸）與y=f（x）的圖像有3個交點，直線y=-b（b<0）與y=f（x）的圖像有4個交點，即方程f（x）=0有3個實根，方程f（x）=-b有4個實根，從而原方程共有7個實根，故答案選C.

例2已知定義在R上的奇函數f（x），滿足f（x-4）=-f（x），且在區間［0，2］上是增函數，若方程f（x）=m（m>0）在區間［-8，8］上有四個不同的根x1，x2，x3，x4，則x1+x2+x3+x4=__________.

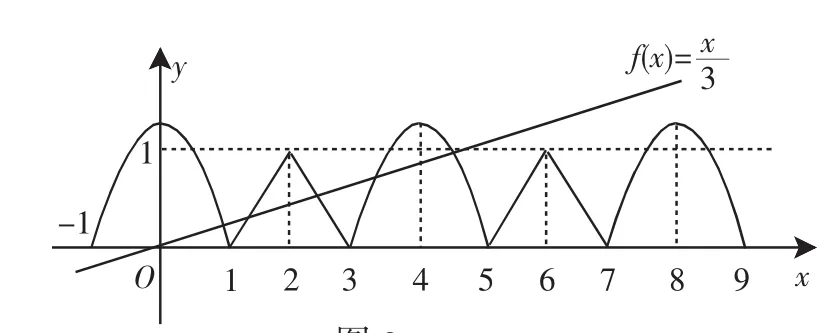
解析：因為定義在R上的奇函數f（x），滿足f（x-4）=-f（x），所以f（x-4）=f（-x）.由f（x）為奇函數，所以函數圖像關于直線x=2對稱且f（0）=0，由f（x-4）=-f（x）知f（x-8）=f（x），所以函數是以8為周期的周期函數.又因為f（x）在區間［0，2］上是增函數，所以f（x）在區間［-2，0］上也是增函數.如圖所示，那么方程f（x）=m（m>0）在區間［-8，8］上有四個不同的根x1，x2，x3，x4，不妨設x1

圖1

圖2

評注：本題綜合考查了函數的奇偶性，單調性，對稱性，周期性，以及由函數圖像解答方程問題，運用數形結合的思想和函數與方程的思想解答問題.

圖3

例4 設a>1，若僅有一個常數c使得對于任意的x∈［a，2a］，都有y∈［a，a2］滿足方程logax+logay=c，這時a的取值的集合為__________.

分析：題目給出的方程中含有x，y，a，c等多個字母，而條件中是對任意的x∈［a，2a］都有y∈［a，a2］，這使我們聯想到函數的定義域、值域，所以必須把方程改寫為關于y的函數，再進一步研究函數的性質.

例5設函數f（x）在（-∞，+∞）上滿足f（2-x）=f（2+x），f（7-x）=f（7+x），且在閉區間［0，7］上，只有f（1）=f（3）=0.

（Ⅰ）試判斷函數y=f（x）的奇偶性.

（Ⅱ）試求方程f（x）=0在閉區間［-2005，2005］上的根的個數，并證明你的結論.

解：（Ⅰ）由f（2-x）=f（2+x），f（7-x）=f（7+x）得函數y=f（x）的對稱軸為x=2和x=7，

從而知函數y=f（x）不是奇函數.

故f（x）在［0，10］和［-10，0］上均有兩個解，從而可知函數y=f（x）在［0，2005］上有402個解，在［-2005，0］上有400個解，所以函數y=f（x）在［-2005，2005］上有802個解.