網構軟件系統中基于信譽激勵的協作博弈模型

印桂生，王姝音，劉杰，董宇欣

(哈爾濱工程大學計算機科學與技術學院，黑龍江哈爾濱150001)

為了解決動態的Internet環境下分散的軟件實體的共享、集成和復用［1-2］，網構軟件這種具有新特征的軟件應運而生，它是一種具有自底向上的自主性、協同性、演化性［3］等特征的軟件新形態，其運行依賴于開放、動態的網絡環境［4］，當前，如何在開放、動態環境下保障網構軟件的可靠性與可信性已經成為信息化社會的重大需求.

網構軟件系統屬于開放網絡環境下的分布式系統，目前，對于分布式系統可信性的研究主要集中在可信管理與可信評估兩方面.可信管理［5］的本質是一種基于認證和授權的訪問控制模型與方法.信任評估模型［6］則是以實體間的推薦信任關系為基礎，結合自身經驗對實體可信度做出評價，然后依據可信度進行決策.信任評估模型主要可分為基于全局信任度模型與基于局部信任度模型.在基于全局信任度的信任模型中［7-9］，節點通過相鄰節點間相互滿意度的迭代獲取其他節點全局的信任度.此類模型往往比較復雜、通信代價高.現有的分布式系統的信任模型大多是局部信任度模型［10-11］，這類模型通過采取局部廣播手段，詢問有限的其他節點以獲取某個節點的可信度.此類模型的典型如PeerTrust模型［12-13］、DyTrust模型［14］等.上述分布式系統中的可信模型在解決網構軟件系統中信任問題時稍顯不足，其原因在于:網構軟件系統中的實體可以根據網絡環境的變化而發生動態演化，具有自組織演化特性.以上模型對于軟件實體的演化性考慮較少.文獻［15］對網構軟件中實體的信任關系進行了形式化建模.文獻［16］則提出了一種面向網構軟件的信任驅動模型，使信任管理和信任關系的在線演化得以實現.以上模型的不足在于在演化過程中不能支持實體間信任關系的自主形成.實際上，網構軟件系統中軟件實體在協作過程中所具有的理性思維使其協作行為呈現出博弈特性.基于此思想，本文提出一種網構軟件系統中實體間的協作博弈模型，利用博弈理論對網構軟件系統中實體節點的協作過程進行分析，建立節點間協作的博弈模型，并在模型中引入實體節點的信譽值，用以建立實體間有效的激勵合作機制，促進實體節點自主進行協作.

1 基于信譽激勵的協作博弈模型

網構軟件的概念最早由我國北京大學的楊芙清教授、梅宏教授所提出.它指的是一種具有柔性、多目標、連續反應式的新系統形態［3］，它能夠根據外部環境變化來動態調節自身參數與指標進而進行演化.網構軟件的基本元素是具有主體化特征的軟件實體，這種軟件實體可以是構件實體、Web服務、軟件Agent等，這種軟件實體以開放、自主的方式存在于Internet的各個節點之上，任何一個軟件實體可在開放的環境下通過某種方式加以發布，并以各種協同方式與其他軟件實體進行跨網絡的互連、互通、協作和聯盟，從而形成一種與當前的信息Web相類似的Software Web.在交互過程中，軟件實體需考慮自身與他人的損失與得益，使得整個交互過程成為一種博弈過程，因此可以用博弈論對網構軟件系統中實體的協作過程進行建模.

1.1 單階段博弈模型(GBM)

在利用博弈理論分析網構軟件系統時，將網絡中的實體看成具有有限理性的博弈參與者，將演化過程中實體協作策略的選擇看成一個復雜的博弈過程，博弈者的策略就是實體節點采取的行動，而參與者的收益函數則是實體節點根據所采取行動而能獲得的收益.根據此思想，首先給出網構軟件系統中實體節點單階段協作博弈的基本式.

定義1 在每個博弈階段，實體節點間的單階段信任博弈可定義為三元組D=(G，S，u).G表示系統中的實體節點集合，也是博弈的參與者:Gi={i，N-i}.其中N-i表示除實體節點i外的其他博弈參與者.S表示參與博弈的實體節點的策略集合S={Si，S-i}，Si={協作，不協作}為實體節點 i所有策略的集合，s={si，s-i}為博弈者的策略組合;u為參與者的收益函數，為在某一時隙t內，博弈者在策略組合下所獲得的收益.

定義2 在某一時隙t內，實體節點i所采取的一系列行動策略表示為表示除i外的其他博弈者的行動策略組合.這種策略的組合關系如表1所示.

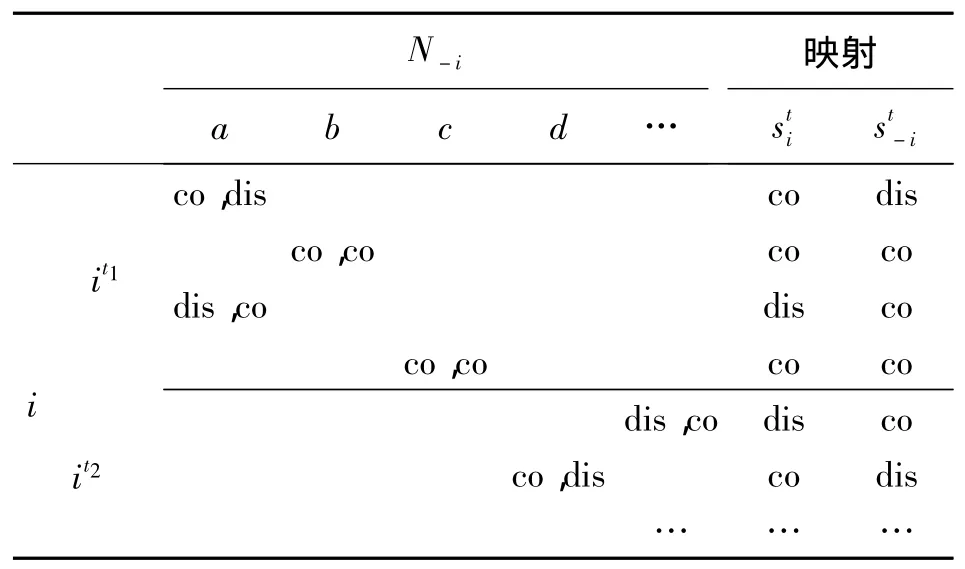
表1 博弈實體策略組合關系表Table 1 The strategy combination relation of the game players

在表1中，a、b、c、d等用來表示除節點 i以外的其他實體節點(統一定義為N-i)，在每個時隙t中，節點i與其他節點分別進行交互，co表示協作(cooperate)，dis表示不協作(dis-cooperate).表1中可以看出，在時隙t1內，節點i的策略組合為{協作，協作，不協作，協作}，與i進行協作的其他節點的策略組合為{不協作，協作，協作，協作}.這里用sti表示由節點i的行動策略組合到實數集的一個映射，即→R，它可以反映出節點i在某一時間段t內采取協作策略的幾率，的取值范圍為［0，1］.值越大，代表實體節點選擇合作的幾率越大.

網構軟件系統中實體節點協作的博弈過程可以描述如下:實體節點在協作的過程中，既可以是協作的發起者，也可以是協作的響應者，例如，實體節點i需要實體節點a提供a的某種服務以完成協作時，i就為協作的發起者，而a為協作的響應者.同時，實體節點a需要節點i的數據以完成該次協作，實體節點a變成協作的發起者，而i變為協作的響應者.這種協作關系類似于P2P關系，即實體節點同時作為客戶端和服務器端進行協作.當實體節點i作為協作的發起者提出協作請求，并得到節點a的協作響應后，由于成功完成一次協作，實體節點i可獲得一定的收益λ，而節點a由于響應實體i的請求，犧牲了一定的資源，并且承擔了i是惡意節點的風險，因此要用掉開銷 ，這里λ＞ρ＞0，λ和ρ均為常量參數.可以看出，如果實體節點i和a在對方提出協作請求時能互相響應對方，則均可獲得收益λ-ρ，如果節點i只獲得其他節點的協作響應，而不去響應其他節點的協作請求時，可以獲得收益λ.同理，如果節點i只響應其他節點的協作請求，而不能獲得其他節點的協作響應時，要付出收益ρ，如果實體節點間互不響應時，其收益均為0.因此，網構軟件系統中實體節點間博弈的收益矩陣可以表示為圖1.

圖1 協作博弈模型的收益矩陣Fig.1 The payoffmatrix of the cooperative game

1.2 博弈模型的Nash均衡

由定義2可知，在時隙t內，除i以外的實體節點選擇協作策略的概率為st-i，選擇不協作策略的概率為1-st-i，因此節點i選擇協作策略的收益為

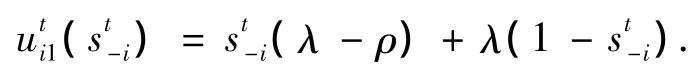
節點i選擇不協作策略的收益為

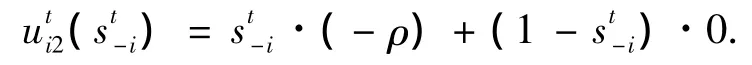
節點i選擇協作策略的概率sti，節點 i選擇不協作策略的概率1-sti，因此實體節點i的期望效用函數可表示為

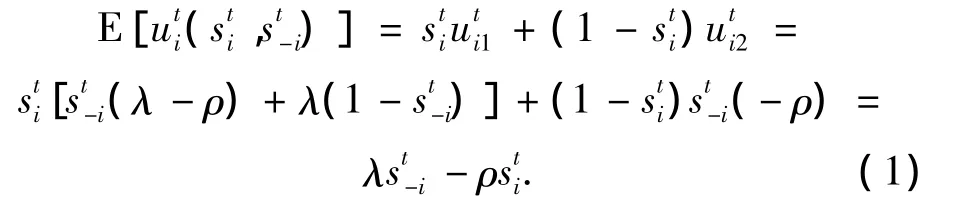
博弈D的Nash均衡為:在給定其他參與者的最優策略st*-i下，能最大化其效用函數的協作博弈策略st*i，即

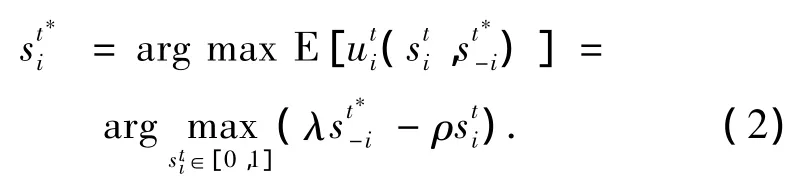
由式(2)可以看出，在博弈的過程中，實體節點的策略選擇可以相互影響和制約.由于實體節點具有自私特性，為追求自身收益最大化，每個節點都會選取較小的sti值，使 ρst

i盡量小，即節點在被請求協作的情況下趨向于選擇“不協作”策略，這時采取“不協作”策略將成為系統中節點的納什均衡策略，而此時系統的整體收益卻接近于零，網構軟件系統的整體性能會受到嚴重的影響，這是一個典型的囚徒困境博弈模型，為了解決該問題，需要通過建立有效的激勵機制來刺激實體節點采取合作行為.

1.3 修正的進化博弈模型(GBDTM)

為了在網構軟件系統中運用博弈理論建立節點間的激勵機制，需要找到一種對所有實體節點都有利的策略，以使實體節點在博弈的過程中最終達成共識，都能獲得較高的收益，從而使整個網絡能夠達到一種Nash均衡狀態［17］，而且保證帕累托有效.

實際上，網構軟件系統還具有下述性質:1)節點的協作行為在時間上具有隨機性及不確定性，即節點可能在任意時刻向其他節點發起或接受到其他節點的協作請求.實體節點之間將重復進行博弈，但各節點并不能確定博弈將在哪一階段結束;2)實體節點對每次協作的結果都有記錄，即實體節點可以掌握博弈的歷史信息.因此，網構軟件系統中實體節點的協作博弈可用進化博弈的思想進行建模.

進化博弈理論中，具有有限理性的參與者在重復博弈的過程中，可以不斷的進行學習并調整策略，以使博弈中參與者最終達成共識，使系統整體的效用最大化.進化博弈的學習過程［18］可以做如下描述:在每一階段的博弈g中，每一個參與者i=1，2，…，N選擇行動ai∈A，每階段博弈產生該階段的收益xi，參與者i可以觀察到一些信息ω∈Ω，而這些信息并沒有被完全預期到，于是參與者通過更新信念規則β:B←Ω來修正自己的信念β°i∈B，最后按照更新后的決策規則f:A←B根據目前的信念再次選擇行動.

為了建立網構軟件系統中實體節點的激勵合作機制，需借鑒進化博弈的思想，即:使參與博弈的實體節點在不斷的重復博弈中總結經驗，動態的學習并調整策略.為了實現實體節點這種動態學習改變策略的博弈過程，并且對實體節點的策略選擇進行激勵，使不合作的節點只能在短期獲得較高的收益值，長期的不合作行為會導致節點收益值減少，這里在原有的網構軟件博弈模型中加入新的要素T，即實體節點綜合信譽值Tt-ii，將該信譽值作為決策者在時刻t觀察到的信息，反饋給博弈實體的收益函數.博弈者在每進行一次博弈后，其綜合信譽值都在發生變化，收益函數受該信譽值影響而改變，因此決定了博弈者行動策略的動態調整.而策略的調整又會使博弈者的信譽值發生變化，該變化作為博弈者新觀察到的信息，來決定下一次的行動.這種通過觀察信譽值變化動態學習調整策略的過程如圖2所示.

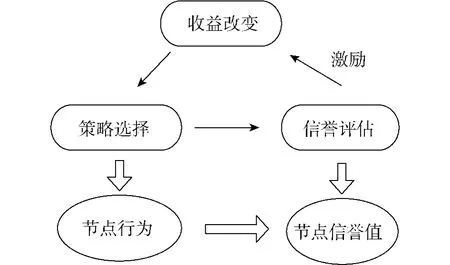
圖2 基于信譽激勵的進化博弈過程Fig.2 The process of evolutionary game based on trust

定義4 在每個博弈階段，基于信譽激勵的進化博弈可定義為四元組 D=(G，S，u，q(·)).G 表示系統中的實體節點集合，也是博弈的參與者:Gi={i，N-i}.其中 N-i表示除實體節點 i外的其他博弈參與者.S表示參與博弈的實體節點的策略集合S={Si，S-i}，Si={sij}為實體節點 i所有策略的集合.s={si，s-i}為博弈者的策略組合;u為參與者的收益函數，ui(si，s-i為博弈者策略組合下所獲得的收益.q(·)為激勵懲罰因子，T為實體節點i的信譽值，T值越大，表示節點i的信譽度越高，T∈［0，1］.

在引入信譽值作為激勵懲罰因子后，網構軟件系統中實體節點協作時的博弈過程可以重新描述為:當實體節點i提出協作請求并得到實體節點a的協作響應后，實體節點i可獲得一定的收益 ，而節點i響應實體節點a的請求，要用掉開銷ρ，同時，實體節點i具有信譽值T，該信譽值作為激勵懲罰因子可動態調節響應協作請求所用的開銷ρ.信譽值高的實體節點更容易獲得其他實體節點提供的服務，因此使其開銷減小，這可以看作是對行為良好的實體節點的獎勵.而信譽值低的節點由于難以獲得其他節點的協作而使其開銷增大，作為對具有不良行為節點的懲罰.因此，網構軟件系統中實體節點間基于信譽激勵的收益矩陣可以表示為圖3.

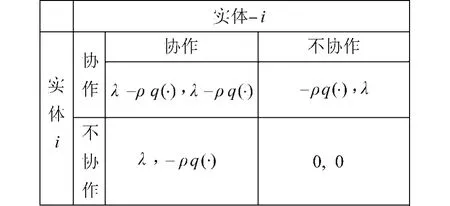
圖3 基于信譽激勵的協作博弈模型的收益矩陣Fig.3 The payoffmatrix of the trust-based cooperative game

定義5 博弈者i在某時隙t內的期望效用函數的修正表達式為

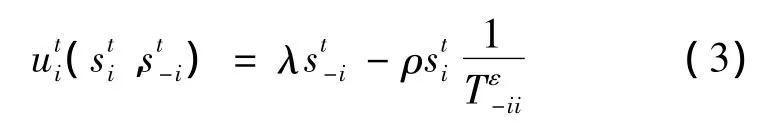
用實體節點的信譽值對節點的收益函數進行修正，可以有效限制節點的自私行為.假若節點i減小選擇協作策略的概率，節點的信譽會降低，反而會增大，根據不同的信譽值評估模型來選定合適的ε值后，節點i單方面減小時，節點 i的最終收益值u也會減小.這樣通過運用信譽值來修正博弈過程中的收益函數，可以有效的激勵實體節點合作.收益函數修正后，如果節點信譽值增加，收益值也會隨之增加，而信譽值較低的節點隨著時間的推移，收益函數值將會不斷降低.

引入激勵懲罰機制對效用函數進行修正后，博弈D的Nash均衡可表示為

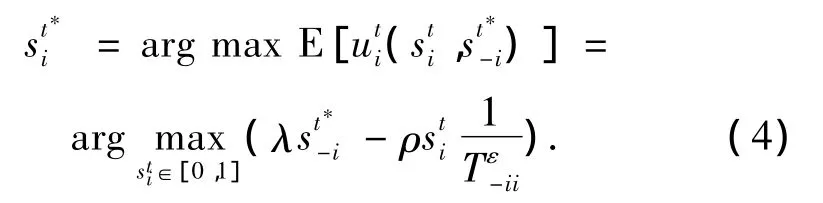
采用激勵機制后，大多數實體節點最終將趨于選擇策略“合作”，網絡將會達到Nash均衡狀態，形成一種節點之間互相合作的網絡系統.

2 信譽值評估模型DyTrust

本文的進化博弈模型中采用DyTrust模型作為信譽值的評估模型，該模型中運用近期信任、長期信任、反饋信任等信任度量的相關參數，增強了節點行為改變的動態適應能力以及對反饋信息的聚合能力.

在時間幀t內，節點j對節點i的信任度量可分為直接信任和間接信任2部分，節點j對節點i的信任度量記為Rtji;則Rt

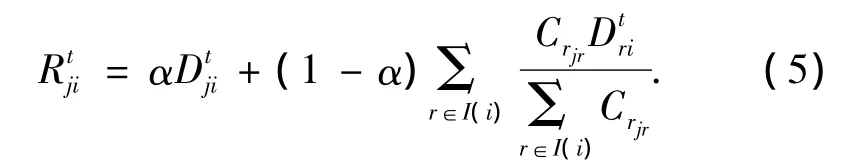
ji可表示為式中:Dtji表示在時間幀t中，節點j對節點i的直接信任;Crjr表示節點j對提供間接信任值的節點r的反饋可信度;I(i)表示時間幀t中，所有和節點i進行過交互的節點集合(不包括節點j);α表示信任評價的信心因子，取值滿足0≤α≤1.

直接信任值可定義為式中:eji為節點j對節點i的交互滿意度的評價，0≤eji≤1;m表示在時間幀t中，節點i和節點j之間交互的總次數.

在經過連續多個時間幀后，節點j對節點i的信任度量可以用節點j對節點i的2個信任度量參數:近期信任、長期信任來表示.

設節點j對節點i的近期信任值STji，該值可定義為

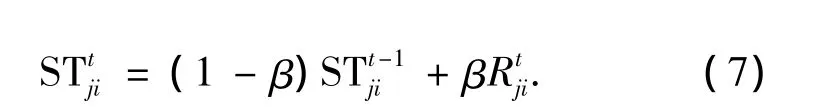
式中:β為信任學習因子，β越大，先前的經驗就越容易被遺忘.

設節點j對節點i的長期信任值LTji，可以利用式(8)進行計算:

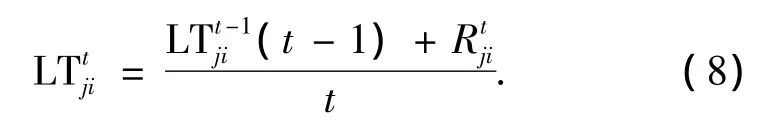
設在時間幀t，節點j和節點r的公共交互節點集合用Cset(j，r)表示，節點j和節點r對公共節點度量的差異dt

ji可以定義為

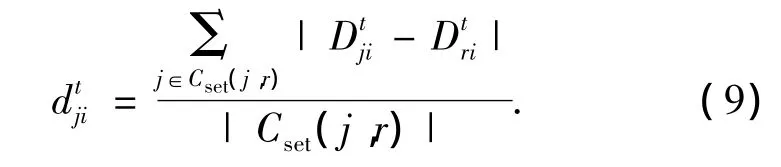
設節點j所能容忍節點r的最大偏差為θ，則反饋可信度的計算公式為

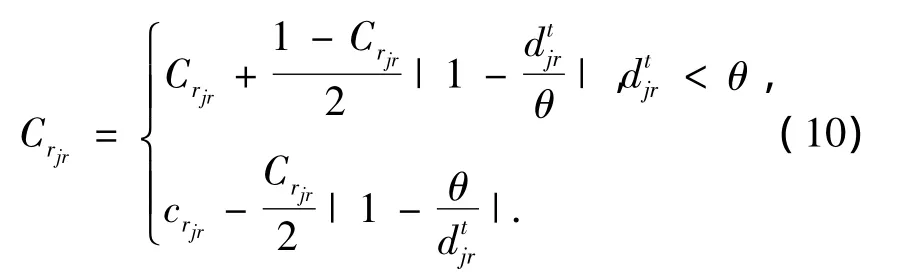
節點r如果提供誠實反饋，會提高其反饋可信度;提供不誠實反饋，則會降低其反饋可信度.

節點j對節點i的信任值Ttji取近期信任值與長期信任值中的較小值，即

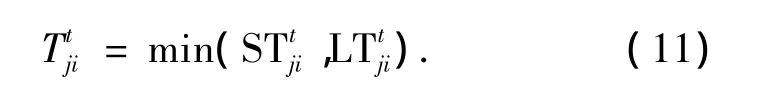
最終，節點i的綜合信譽值是在某一時間段里，與i有過交互歷史的節點對節點i做出的綜合評價.可表示為式中:Cset(-i)表示時間幀t內，與節點i有過交互的節點的集合.

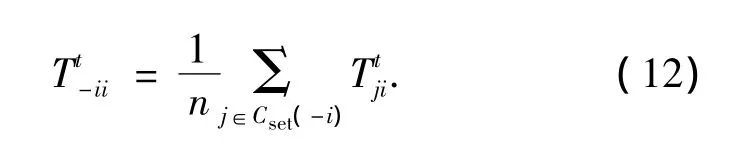
利用DyTrust信任評估模型得出節點i的綜合信譽值T，作為進化博弈模型中的參數，有效的將DyTrust信任模型的反饋控制機制與進化博弈論中的節點激勵機制相結合，不但可以增強信任模型的動態適應能力，還可以促進網構系統中的構件節點自主的進行協作.這是單純使用DyTrust信任模型所不能解決的.

3 實驗驗證

本文對上述GBDTM模型進行了試驗仿真.模擬實驗初步驗證了該修正模型的合理性.模擬實驗初始場景中，在局域網上，設置了500個節點，要求每一個節點都分別通過無激勵的博弈方法、基于DyTrust信任評估方法、以及GBDTM方法進行協作交互.

設效用函數中參數 ε=3，λ=120，ρ=80，α=0.5，β =0.5，博弈交互重復100 次.圖4 為3 種方法成功交互次數數目對比圖，其中，DyTrust表示用無激勵的博弈方法進行交互;GBDTM表示用GBDTM方法進行交互.從圖中可以看出，利用無激勵博弈方式進行交互時，隨著交互總次數的增加，成功交互次數反而下降，這充分證明了非合作博弈中節點存在“自私”行為.在利用DyTrust模型進行交互時，隨著交互次數的增加，節點的交互成功次數不斷波動，DyTrust模型能有效反應網絡節點的信任值，使網絡節點在進行交互前對潛合作對象做出有效判斷，但是，并不能促進網絡中各節點進行成功交互.在利用GBDTM方法進行交互時，隨著交互次數的增加，成功交互次數呈現出上升態勢，并最終趨于穩定.可見，建立節點間激勵機制，能夠促使節點選擇信任策略來進行博弈，從而達到節點間的有效合作，使網絡趨向穩定，提高網絡的安全性.

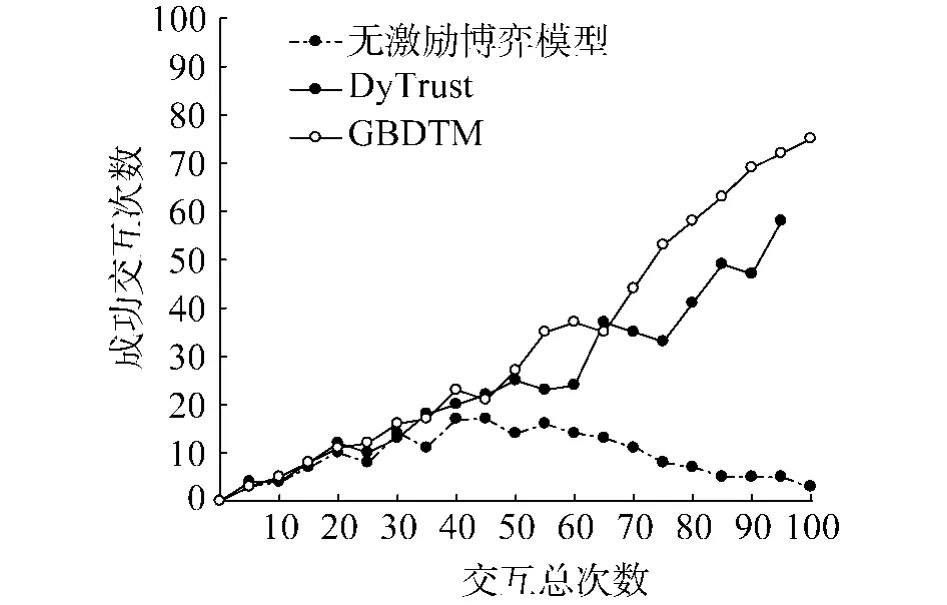
圖4 成功交互次數數目對比Fig.4 The comparison diagramof successful interaction times

圖5反映了隨著博弈次數的增加，在無激勵博弈模型與GBDTM模型中，選擇合作策略的節點在數量上的變化.從圖中可以看出采用不同的信任模型，實體節點策略的調整有著明顯的變化，GBDTM模型中選擇合作策略的節點數目不斷增長，并在博弈的后期趨于一個穩定的數目，達到Nash均衡狀態.而無激勵博弈模型卻使選擇合作策略的實體節點數目不斷減少，最終下降到一個很低的水平.

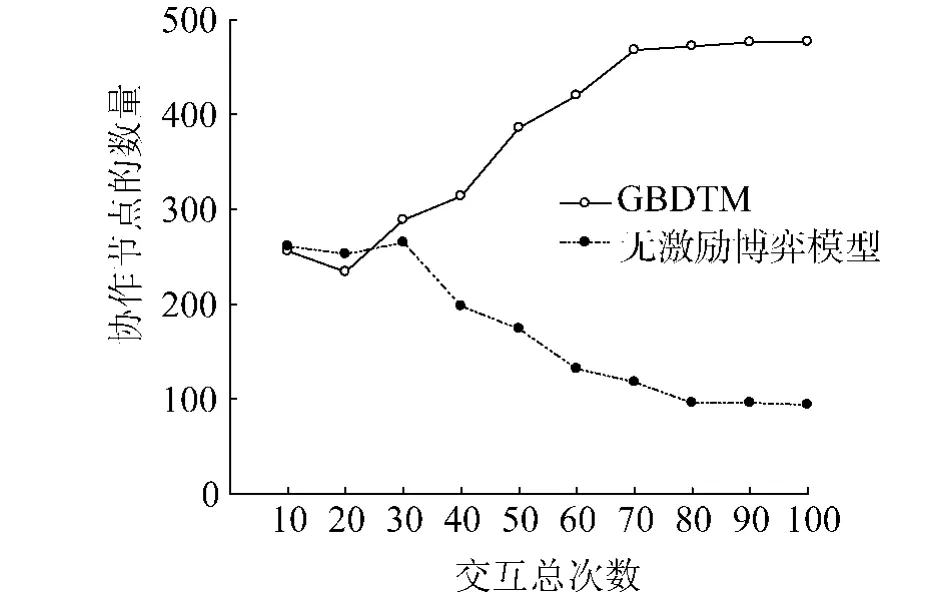
圖5 成功交互節點數目對比Fig.5 The comparison diagramof successful interaction nodes

圖6可以看出隨著成功交互次數的增加，在無激勵博弈模型與GBDTM模型中，實體節點分別得到的收益值的變化.實體節點在無激勵的博弈過程中，能成功交互的次數很少，即使成功交互，也不能獲得很好的收益值.GBDTM模型中，隨著成功交互次數的增多，節點的信譽值不斷提高，因此節點收益值也隨之上升.同時促使實體節點在下一次策略選擇時更容易選擇合作行為，在這種信譽值與效用值互相促進的情況下，形成一種“良性循環”.

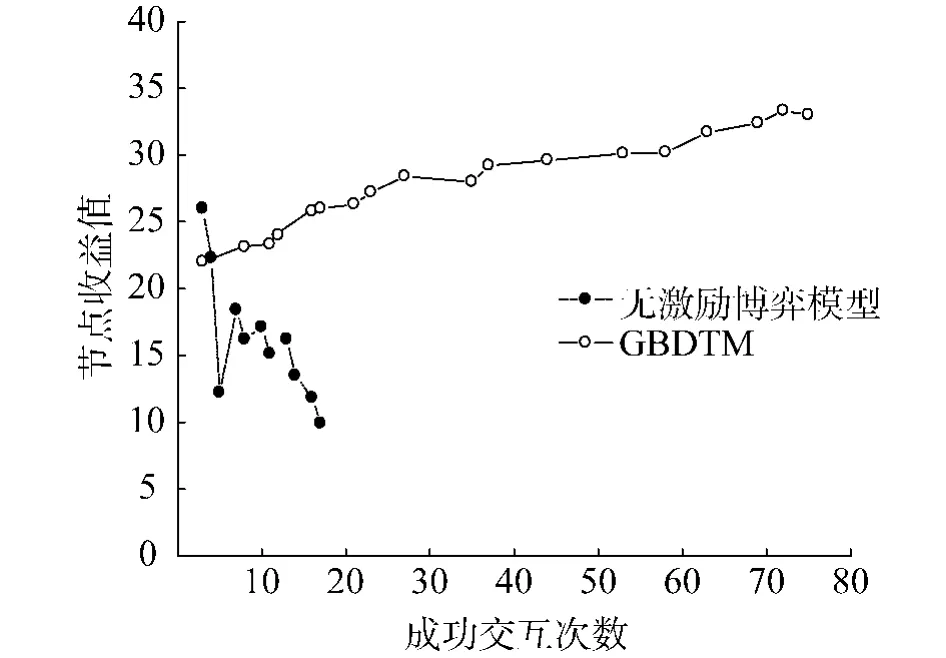
圖6 收益值對比Fig.6 The comparison diagramof utility

4 結束語

在實體節點交互過程中建立激勵合作機制，可防止及克服節點自私行為的不斷發生，以保證網構軟件系統基本功能的正常運行.本文結合當前對于博弈論中激勵合作機制的研究，提出了一種新的博弈理論與DyTrust信任模型相結合的GBDTM模型，該模型通過對效用函數的修正，可有效的促進實體節點之間通過博弈自主的形成協作關系，經理論分析證明以及實驗驗證，得出函數修正后的有效性，說明了該方法性能的優劣，為提高網構軟件系統的整體安全性奠定了基礎.

［1］SHAwM.Self-healing:softening precision to avoid brittleness［C］//Proceeding of the 1st ACmSIGSOFTWorkshopon Self-Healing Systems.Charleston，USA，2002:111-113.

［2］MEIH，HUANG K，ZHAO H Y，et al.A software architecture centric engineering approach for internetware［J］.Science in China:Series E，2006，36(10):1100-1126.

［3］楊芙清.軟件工程技術發展思索［J］.軟件學報，2005，16(1):1-7.YANG Fuqing.The speculation of software technology de-velopment［J］.Journal of Software，2005，16(1):1-7.

［4］呂建，馬曉星，陶先平，等.網構軟件的研究與進展［J］.中國科學:E輯，2006，36(10):1037-1080.Lü Jian，MA Xiaoxing，TAO Xianping，et al.The research and development of Internetware［J］.Science in China:Series E，2006，36(10):1037-1080.

［5］BLAZE M，FEIGENBAUmJ，LACY J.Decentralized trust management［C］//Proceedings of the 1996 IEEE Sympon Security and Privacy. Washington DC， USA， 1996:164-173.

［6］ABDUL-RAHMAN A，HAILESS.A distributed trustmodel［C］//Proceedings of the 1997 NewSecurity Paradigms Workshop.Cambria，United kingdom，1998:48-60.

［7］KAMVAR SD，SCHLOSSER mT，GARCIA-MOLINA H.The eigen trust algorithmfor reputation management in P2pnetworks［C］//Proceedings of the 12th International Conference on World Wide Web.Budapest，Hungary，2003:640-651.

［8］竇文，王懷民，賈焰，等.構造基于推薦的peer-to-peer環境下的 Trust模型［J］.軟件學報，2004，15(4):571-583.DOUWen，WANG Huaimin，JIA Yan，etal.A Trustmodel based on reputation in P2pnetworks［J］.Journal of Software，2004，15(4):571-583.

［9］YAMAMOTO A，ASAHARA D，ITAO T.Distributed pagerank:a distributed reputationmodel for open P2pnetworks［C］//Proceedings of International Symposiumon Applications and the Internet Workshops.Tokyo，Japan，2004:389-396.

［10］MARTIS，GARCIA-MOLINA H.Limited reputation sharing in P2psystems［C］//Proceedings of the 5th ACmConference Electronic Commerce. NewYork， USA，2004:91.

［11］LEE S，SHERWOOD R，BHATTACHARJEE B.Cooperative peer groups in NICE［J］.Computing Networks，2006，50(4):523.

［12］XIONG L，LIU L.PeerTrust:supporting reputation based trust for peer to peer electronic communities［J］.IEEE Transactions on Data and Knowledge Engineering，Special Issue on Peer to Peer based Data Management，2004，16(7):843-857.

［13］SRIVATSA M，XIONG L，LIU L.TrustGuard:countering vulnerabilitles in reputation management for decentralized overlay networks［C］//Proceedings of the 14th World Wide Web Conference(WWw2005).Chiba，Japan，2005:422-431.

［14］常俊勝，王懷民，尹剛.Dytrust:一種P2P系統中基于時間幀的動態信任模型［J］.計算機學報，2006，8(29):1301-1307.CHANG Junsheng，WANG Huaiming，YIN Gang.DyTrust:a time-frame based dynamic trust model for P2psystems［J］.Journal of Computers，2006，8(29):1301-1307.

［15］董宇欣，印桂生，謝新強.網構軟件信任機制的形式化研究［J］.哈爾濱工程大學學報，2011，6(32):800-806.DONG Yuxin，YIN Guisheng，XIE Xinqiang.Study on formalization of trustmechanismfor Internetware［J］.Journal of Harbin Engineering University，2011，6(32):800-806.

［16］馬志強，印桂生.面向網構軟件的信任驅動及演化模型［J］.哈爾濱工程大學學報，2010，8(31):1054-1060.MA Zhiqiang，YIN Guisheng.A trust-driven evolutionary model for Internetware［J］.Journal of Harbin Engineering University，2010，8(31):1054-1060.

［17］VON NEUMANN J，MORGENSTERN O.Theory of games and economic behavior［M］.Princeton:Princeton University Press，1994，328:36-39.

［18］FUDENBERG D，LEVINE D K.The theory of learning in games［M］.［S.l.］:MIT Press，1998，78:167-169.