基于利益相關者理論的投保人與保險人的博弈分析

楊衛平，陸鳳順

（湖南大學 金融與統計學院，湖南 長沙 410006）＊

一、引 言

作為當前西方經濟學界和管理學界研究的熱點理論之一——利益相關者理論，對傳統股東利益至上的觀點提出了挑戰，認為企業是一系列包括股東、管理者、雇員、債權人、供應商、客戶等利益相關者之間的多邊契約，各利益相關者彼此之間形成一個利益共同體，以自身所擁有的人力資本或非人力資本進行合作，應對外部不確定性環境所帶來的風險［1］。依據利益相關者理論，壽險公司的股東、管理者、員工等都是公司的利益相關者，此外，投保人也是壽險企業的主要利益相關者，因為投保人既是壽險公司的消費者，又是與公司長期發展息息相關的主要債權人［2］。目前國內學者對利益相關者理論在保險行業中的運用研究，多集中于對逆選擇和道德風險的博弈分析［3，4，6］或是某個險種相關方的利益博弈分析［5，7］，側重對保險公司及其股東利益的保護，而從保護投保人利益角度研究的較少，缺乏對弱勢利益相關方利益的關注，特別是對投保人的利益關注不足。

二、保險公司利益相關者的利益需求及其沖突

保險公司的股東、管理者和投保人都是公司的利益相關者，但利益需求各有不同。股東和經營者代表公司的利益，關注的是高額利潤和資本的回報，作為利益共同體，經營者為股東利益服務。保險企業是典型的負債經營企業，尤其在壽險公司，壽險合同大多有長期性和持續性的特點，因此，投保人不僅關注公司能否提供優質的產品和服務、合理的產品價格，還關注公司在長期內能否有效履行壽險合同的保障和給付責任。在保險企業經營的過程中，為了獲得更高的利潤和資本回報，就可能產生危及投保人利益的行為，例如在發生保險事故時，基于晦澀難懂的保單條款作出不利于被保險人的解釋；可能采取更激進型投資策略，危害公司償付能力，從而損害投保人的長期利益等等。公司和投保人之間利益的沖突，是由于各自追求的利益不同。我國保險業起步較晚，使得大多數保險公司仍把短期邊際利潤作為企業的唯一目標，不注重利益相關者特別是投保人利益的保護，兩者的利益沖突問題尤為突出。

三、保險人與投保人的利益博弈分析

（一）靜態博弈分析

1.完全信息靜態博弈

（1）建模前提：第一，博弈中代表保險人利益的股東是指對公司的利潤擁有控制權并對公司的重大事件具有話語權的控制股東，并非指小股東。第二，假設控制股東和經營者已經成為一個利益共同體，即控制股東和經營者利用自己在信息和管理等方面的優勢合謀，在博弈模型中將這一利益共同體簡稱為保險人，將投保人、被保險人和受益人這一利益共同體稱為投保人。第三，博弈的局中人——保險人和投保人都是理性人，風險態度是風險規避，在客觀條件約束下作出使自身利益或效用最大化的決策。第四，博弈雙方的策略空間、特征、支付函數及博弈結構等是共知的。

（2）模型假定：第一，假定為單階段的靜態博弈。即保險人和投保人雖然不是同時采取行動，但是對于保險人的行為，投保人可以觀察到，并作出反應。第二，博弈的局中人為保險人和投保人。保險人的策略空間為侵害投保人利益、不侵害投保人利益；投保人的策略空間為投保、不投保。第三，博弈基本參數假設如下：X為投保人選擇投保時需繳納保費；Y為投保人在保險人不侵害其利益時可以獲得正常收益（包括賠償金及分紅等投保人理應獲得的收益）；C為投保人在保險人侵害其利益時獲得的收益，（因為保險人可能以投保人不具有可保利益或其他理由拒絕賠償保險金，還有可能減少分紅等，使投保人的收益低于正常情況下的收益）；D為保險人在不侵害投保人利益時可以獲得的正常收益；T為保險人在侵害投保人利益時可以獲得除D以外的額外凈收益（此額外凈收益為額外收益減去因侵害支付的成本后的凈收益，T＞0）；P3為投保人不將資金用于投保，而將投保費用投資于資本市場可獲得的收益，即投保費用的機會成本。保險人侵害投保人利益，投保人選擇不投保時，保險人不能獲得承保利潤和投資收益等收益，但仍需支付侵害造成的成本，包括帶來的公司名譽損失E，以及被監管部門查處的罰金F（這里把監管部門對保險人的處罰統稱為罰金）。保險人不侵害投保人利益，投保人仍選擇不投保時，保險人的收益為－H。建立靜態博弈，二者的收益矩陣如表1所示，括號中第一個值表示投保人的收益，第二個值表示保險人的收益。

表1 保險人與投保人的收益矩陣

需要說明的是，現實情況中有（－X＋Y）＜P3＜（－X＋C）。因為倘若保險人侵害投保人的利益，例如在投保人索賠時，保險人以投保人不具有可保利益或其他理由拒絕賠償保險金，投保人則可能拿不到保險金或只能拿到一小部分退保費，故有（－X＋Y）＜P3；而在投保人利益不被侵害時，投保人可以拿到正常額度的保險金，使得P3＜（－X＋C），此時投保人才有動力把錢從資本市場取出用以購買保險。

為了討論簡便，再設P1＝－X＋Y，P2＝－X＋C，M1＝X＋D－Y＋T，M2＝X＋D－Y，G1＝－EF＜0，G2＝－H＜0。P1即保險人侵害投保人利益時投保人投保的收益，P2即保險人不侵害時投保人投保的收益，M1即保險人侵害時投保人投保保險人的收益，M2即保險人不侵害時投保人投保保險人的收益，G1即保險人侵害投保人不投保保險人收益，G2即保險人不侵害投保人不投保保險人收益。則以上收益矩陣可簡化為表2所示。

表2 保險人與投保人的收益矩陣

（3）模型求解。在完全信息條件下，利用劃線法尋找以上收益矩陣的納什均衡：第一種情況：G1＞G2時，由以上討論可知M1＞M2（因為M1＝M2＋T且T＞0），保險人最佳策略是侵害，故在M1下面劃一橫線；同理，在投保人選擇不投保時，保險人最佳策略是侵害，在G1下劃線，可知保險人的占優策略是“侵害”。當保險人侵害投保人利益時，投保人的最佳策略是不投保，在P3下劃線；當保險人不侵害投保人利益時，投保人的最佳策略是投保，在P2下劃線，此時有唯一的納什均衡策略（不投保，侵害）。從上可知，M1、G1下都劃線，說明保險人的占優策略是“侵害”，也就是說，不管投保人是否投保，保險人選擇侵害都比不侵害能獲得更大的收益，那么，保險人就沒有動力維護投保人的利益，而在保險人選擇侵害時，投保人最佳的選擇就是不投保。因此，在完全信息條件下，保險人為了使自己利益最大化，沒有動力去保護投保人的利益，投保人也將會選擇退出保險市場。第二種情況：G1≤G2時，用劃線法可知該博弈矩陣不存在納什均衡策略。

2.不完全信息靜態博弈。現實中的情況是，由于信息不對稱，投保人并不確定保險人是否會侵害自己的利益，但知道保險人侵害的概率為α，不侵害的概率為1－α，保險人只能知道投保人投保的概率為β，不投保的概率為1－β，那么對投保人而言，選擇投保時的期望收益：U1＝αP1＋（1－α）P2；選擇不投保時的期望收益：U2＝αP3＋（1－α）P3＝P3；總收益：U0＝βU1＋（1－β）U2＝αβP1－αβP2＋βP2－βP3＋P3。對收益函數求導：即對投保人來說，當保險人侵害其利益的概率大于α時，投保人的最優選擇是不投保；當保險人侵害的概率小于α時，投保人的最優選擇是投保，即當保險人侵害的概率等于α時，投保人選擇投保或不投保效用是一樣的。

對保險人而言，侵害投保人利益時的收益為：E1＝βM1＋（1－β）G1；不侵害投保人利益時的收益為：E2＝βM2＋（1－β）G2；總收益為：E0＝αE1＋（1－α）E2＝αβM1＋αG1－αβG1－αβM2－αG2＋αβG2＋βM2＋G2－βG2。對收益函數求導：

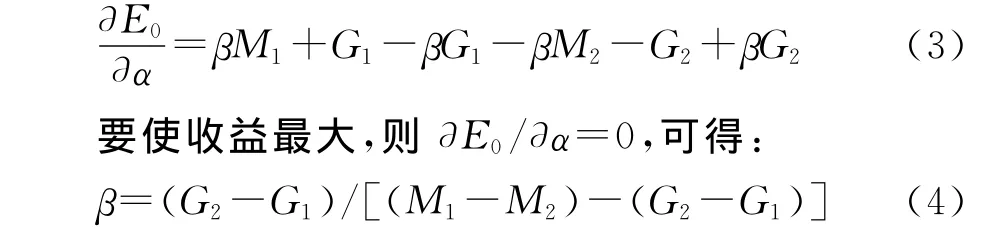
即當投保人選擇投保的概率大于β時，保險人的最優選擇是侵害；當投保人選擇投保的概率小于β時，保險人的最優選擇是不侵害；當投保人選擇投保的概率等于β時，保險人侵害或不侵害投保人的收益是一樣的。

博弈的混合策略納什均衡解是：保險人侵害的最優概率為α，投保人選擇投保的最優概率為β。P2越大，α越小，即投保人在利益不被侵害時可以獲得的收益越大，其要求保險人不侵害的概率越小；M1－M2＝T越大，β越小，即保險人侵害投保人時得到的不當得利越大，投保人投保的意愿會降低；G2－G1越大，β越大，即保險人將受到監管部門的監管和處罰力度越嚴厲，投保人選擇投保的概率會越大。

（二）完全信息動態博弈模型

1.單一階段動態博弈。單一階段的動態博弈屬于非合作博弈，假設保險人和投保人都是理性人，作出的選擇都是使自己效用最大化為目標。兩者之間的博弈是完全信息動態博弈，行動有先后順序：首先，投保人選擇是否購買該保險人提供的保險產品（假設投保人購買保險時即繳納保費）；其次，保險人選擇提供高質量或是低質量的產品和服務。投保人購買保險時通常保險人都會承諾客戶至上，例如承諾在保單存續期間提供優質服務、發生保險事故時提供快速有效的理賠或人身補償，類似行為稱為提供“高質量產品和服務”，但現實中投保人繳納了保費之后，保險人有可能不履行合同簽訂時許下的承諾，例如出險時將事故列為除外責任或以各種理由延緩賠付速度甚至降低保險金額度，類似行為稱為“低質量的產品和服務”。

為了簡便，稱保險人為A，投保人為B，首先，B選擇是否購買A提供的保險，然后A選擇是否提供優質產品和服務。倘若B不購買保險，效用為0（不能從保險合同中獲得效用），倘若購買到高質量的產品和服務，效用為＋I1，購買到低質量的產品和服務的效用為－I2，A提供高質量產品和服務可獲利潤＋R1，提供低質量時獲利潤＋R2，其中I1、I2、R1、R2＞0，且I1＞I2，R2＞R1，該博弈的擴展式表述如下：

如圖1，在一次性博弈中，利用逆推退歸納法可知，在第二階段如果B選擇投保于A，A的最優策略是提供低質量產品和服務，此時A可獲得利潤＋R2（A選擇高質量只能獲得利潤＋R1，而R2＞R1），B獲得的效用為－I2＜0；再逆推至第一階段，因為B知道如果自己選擇投保，A將在第二階段選擇低質量，因此B在追求自身利益最大化的理性假設下，第一階段的最優選擇是不投保（因為選擇不投保可得到的效用為0，大于第二階段的效用－I2），由此可知，均衡結果是B在第一階段選擇不投保結束博弈，博弈的子博弈精煉納什均衡是（不投保，低質量），即保險人提供低質量的產品和服務，投保人選擇不購買保險。若B投保，A提供高質量，則A、B都可獲得較高的收益（＋I1，＋R1）。

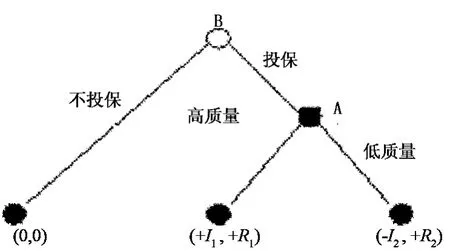
圖1 一次性博弈A，B的效用

2.重復博弈。在一次性博弈中，參與人只考慮當期自己可獲得的最大收益，無需考慮長期，但是在現實保險市場中，保險人需要考慮長遠利益，把保持名譽視作長期利益，因為好的名譽會吸引更多的人加入保險。保險人和投保人之間的動態博弈可以用重復博弈進行分析，這一模型解釋如下：

在保險市場交易中，保險人是長期的固定參與人，不斷重復提供保險產品，而消費者即投保人是不固定的，為簡單起見，假定只有一個保險人A提供保險產品，潛在投保人有B1，B2，B3…，Bn，每個階段只有一個投保人且每人只購買一次保險產品。A首先與B1博弈，然后與B2，以此類推至Bn，Bn在決定是否投保于A時，了解A的歷史，即了解A提供給之前投保人的產品和服務的質量，如果Bn了解到A之前為Bn－1個投保人提供的是低質量，A的名譽敗壞且不能回復，Bn也不再購買保險。B1，B2，B3…，Bn只關心自己的利益，A與B1，B2，B3…，Bn博弈的收益分別為U1，U2，U3…，Un，A的總收益 U（n）是所有階段博弈收益折現值之和，即：

U（n）＝U1＋εU2＋ε2U3＋…＋εn－1Un，其中ε表示貼現值。

在一次性博弈中，我們已經討論了唯一的納什均衡是（不投保，低質量）。但是在無限次博弈中，博弈過程沒有最后階段，不能采用逆向歸納法求解，A不僅僅要考慮短期收益，更要注重其長期收益。在第一階段，B1選擇投保，如果A提供高質量的產品和服務，隨后的B2B3…Bn會愿意繼續投保；如果A提供低質量產品和服務，之后的潛在投保人將不再投保。均衡結果是（投保，高質量），此時每個投保人得到的效用為＋I1，A每一階段得到的平均效用為＋R1，對均衡結果分析如下：

（1）A選擇高質量是最優策略。因為A如果選擇提供低質量，可以得到的效用為R2，但在之后每階段的效用為0（因為之后不再有投保人購買保險），如果總是提供高質量的產品和服務，每階段得到效用R1，效用總和為：

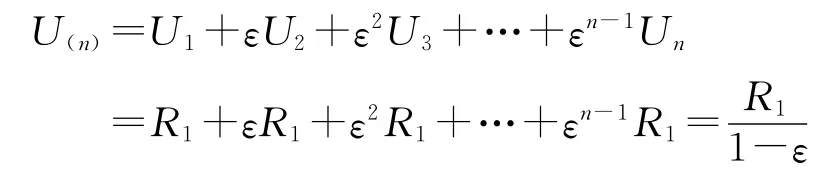
因此，如果保險人提供高質量的總效用R1／（1－ε）大于提供低質量時的效用R2，即ε＞（R2－R1）／R2時，保險人就不該選擇提供低質量產品和服務。

（2）對于B，假定ε＞（R2－R1）／R2。B只關心自己得到的效用，當預期得到高質量產品和服務時才會投保；B預期不曾提供低質量的保險人將會繼續提供高質量，所以選擇投保是最優的；如果B了解到A提供過低質量的產品和服務，預期A將繼續提供低質量，此時不購買是最優的。

四、總結與啟示

由以上博弈結果分析可知，投保人作為保險企業的消費者和債權人，其利益的保護和保險企業的長期發展息息相關。如果投保人利益得不到有效的保障，投保人會選擇退出保險市場，這將影響到保險企業的市場占有率、良好的企業信譽和形象等等，給保險企業的長期健康發展帶來威脅。因此，保險企業在經營過程中要注重有效保護處于弱勢地位的投保人的利益，平衡兩者之間的利益關系。保險人應該把保持名譽視作長期利益，以客戶為導向，在保險條款的解釋上更明晰，費率厘定更科學，提供高質量的保險產品和服務，形成良性循環。此外，有效保護投保人的利益，還需要監管部門加大對保險企業的監管力度和處罰力度，以降低保險企業侵害投保人利益的動機，從而有效保護投保人的利益。

［1］陳宏輝.企業的利益相關者理論與實證研究.浙江大學博士論文［D］.2003.

［2］彭雪梅.保險會計學［M］.成都：西南財經大學出版社.2010：6－7.

［3］顧力.我國保險市場的信息不對稱問題研究［D］，浙江大學碩士學位論文，2005.

［4］陳桂柳.保險市場非對稱信息的博弈分析［D］，廈門大學碩士學位論文，2006.

［5］張嬌.商業健康保險中道德風險的博弈分析［D］，復旦大學碩士學位論文，2007.

［6］楊美琴，龔日朝.保險公司與投保人的靜態博弈分析［J］，南華大學學報，2008，（4）：76－82.

［7］黃亞林.農業保險市場利益相關者的博弈分析［J］，金融發展研究，2009，（2）：80－83.