基于Matlab/Simulink的航空發(fā)動機(jī)部件級建模與分析

夏 超，王繼強(qiáng)，商國軍，周 淼

（南京航空航天大學(xué)能源與動力學(xué)院，南京 210016）

0 引言

在航空發(fā)動機(jī)部件級建模中，非線性微分方程組和平衡方程的求解多采用迭代計算，但是在計算動態(tài)模型時，動態(tài)因素的存在使得迭代次數(shù)大大增加，模型實時性和全包線內(nèi)的收斂均很難得到保證[1]。

為了解決部件級建模中解非線性方程組時的迭代問題，引入容積動力效應(yīng)，在Matlab/Simulink中搭建航空發(fā)動機(jī)的無迭代動態(tài)模型，最后與GSP軟件仿真的結(jié)果進(jìn)行比較，驗證了該模型有效且準(zhǔn)確。

1 基于Matlab/Simulink的渦扇發(fā)動機(jī)數(shù)學(xué)模型

1個完整的渦扇發(fā)動機(jī)模型包括進(jìn)氣道、風(fēng)扇、外涵道、壓氣機(jī)、燃燒室、高壓渦輪、低壓渦輪、混合室、噴管以及大氣環(huán)境等大模塊，并形成各自獨立的子模塊。各模塊之間通過氣流的流向及匹配關(guān)系連接。所搭建的完整發(fā)動機(jī)Simulink方框圖如圖1所示，作為比較的發(fā)動機(jī)GSP自帶的某模型方框圖如圖2所示。

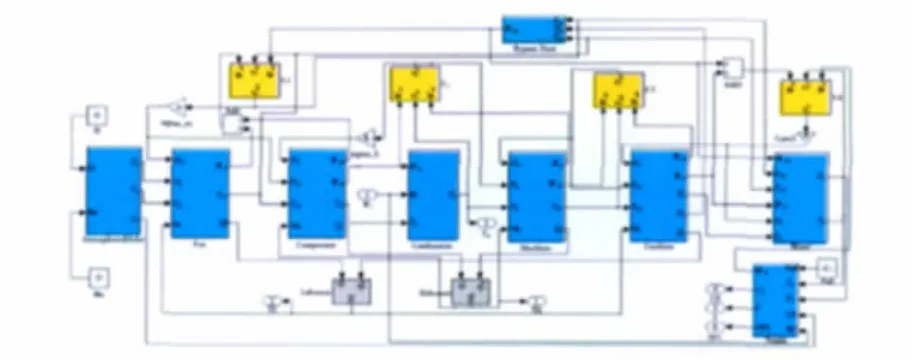
圖1 完整的發(fā)動機(jī)Simulink方框圖

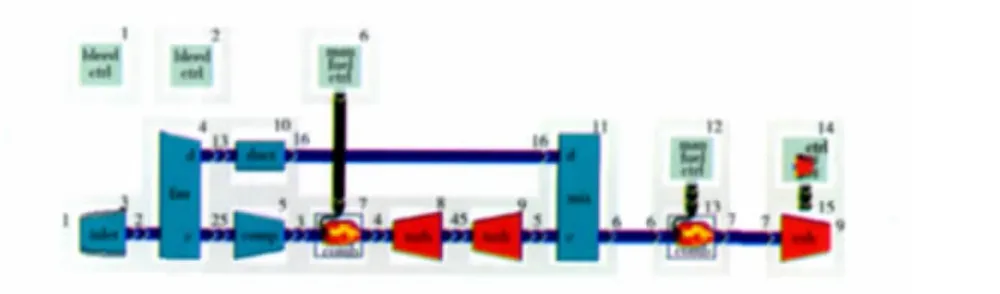
圖2 發(fā)動機(jī)GSP方框圖

2 發(fā)動機(jī)的動態(tài)仿真

對于航空發(fā)動機(jī)來說，動態(tài)仿真指發(fā)動機(jī)加、減速等動態(tài)過程。一般在發(fā)動機(jī)動態(tài)仿真中，忽略容積動力學(xué)效應(yīng)和熱慣性，假定在動態(tài)過程中滿足流量準(zhǔn)平衡，由于模型在運行中要反復(fù)運行雅可比矩陣，計算量巨大難以達(dá)到實時性。本文采用考慮容積動力效應(yīng)的無迭代方法，即在動態(tài)仿真中引入容積效應(yīng)，認(rèn)為動態(tài)時流量不再平衡，壓力隨流量變化而變化[2]。

進(jìn)行動態(tài)仿真時，采用GSP軟件中1個模型的數(shù)據(jù)，利用本文建立的發(fā)動機(jī)模型進(jìn)行仿真，最后與GSP軟件仿真的結(jié)果進(jìn)行比較，以驗證該模型的準(zhǔn)確性。

2.1 考慮容積動力效應(yīng)的無迭代方法

考慮容積動力效應(yīng)的渦扇發(fā)動機(jī)方框圖如圖3所示。

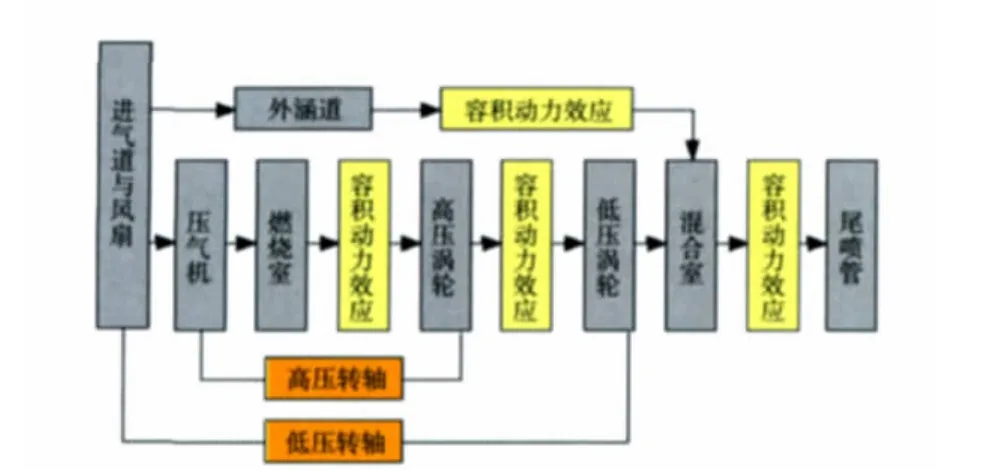
圖3 考慮容積動力效應(yīng)的渦扇發(fā)動機(jī)方框圖

在動態(tài)過程中，由于容腔內(nèi)氣體質(zhì)量與能量的積聚和釋放而引起壓力變化，氣流的進(jìn)、出口參數(shù)不再相等，且滿足一定的動力學(xué)方程。該動力學(xué)方程包括質(zhì)量與能量方程，其中質(zhì)量方程占主導(dǎo)，本文為了簡化計算，僅考慮質(zhì)量方程[3]。

假設(shè) 1 股總溫、總壓、流量分別為 Ti、Pi、Wai的氣流流入容腔，以 To、Po、Wao流出，對于單輸入、單輸出的容腔僅考慮質(zhì)量方程可描述為

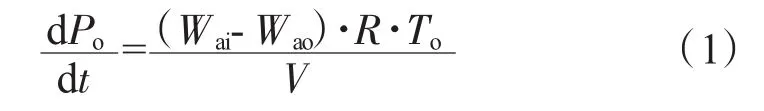
式中：R為氣體常數(shù)；V為容腔體積[4]。

由于渦扇發(fā)動機(jī)流路計算選用了4個壓比（分別為πf、πc、πt，h、πt，l），故選用外涵道容腔（I）、燃燒室容腔（II）、高低壓渦輪之間的容腔（III）和混合室容腔（IV）4個容腔分別求取對應(yīng)的壓比。描述4個容腔的容積動力學(xué)方程為

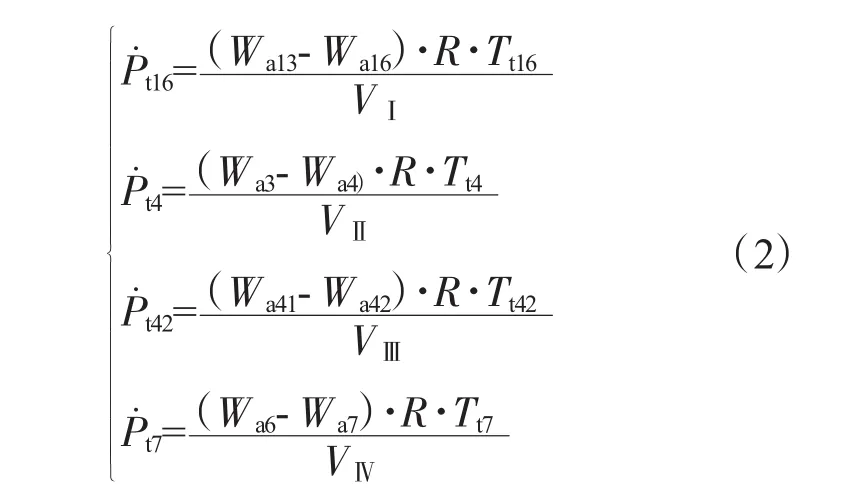
給定初始條件便可以積分求解 Pt16、Pt4、Pt42、Pt7。已知Pt16可以求得 Pt13、Pt21、Pt22，Pt21=Pt22=Pt13=Pt16/σbp；已知 Pt4可以求得 Pt3，Pt3=Pt4/σb；已知 Pt42可以求得 Pt41，Pt41=Pt42;Pt3，Pt3=Pt4/σb； 已 知 Pt7可 以 求 得 Pt55，Pt55=（Pt7Wa7/σm-Pt16Wa16）/Wa55。則 4 個壓比分別為

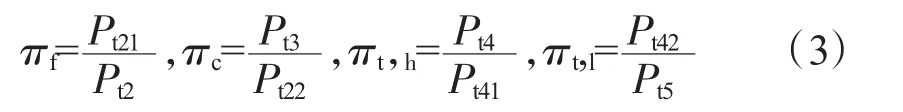
另外，再考慮2個轉(zhuǎn)子動力學(xué)方程

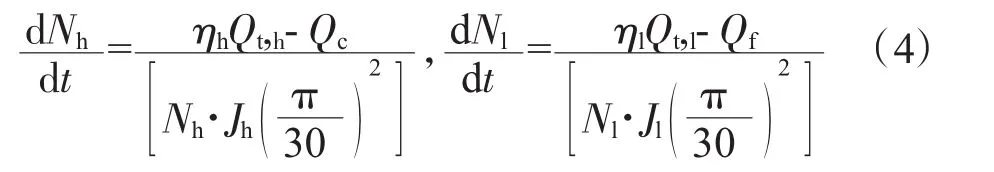
式中：Qt，h、Qt,l分別為高、低壓渦輪輸出功率；ηh、ηl分別為高、低壓轉(zhuǎn)軸的機(jī)械效率；Jh、Jl分別為高低壓轉(zhuǎn)軸轉(zhuǎn)動慣量；Qc、Qf分別為壓氣機(jī)和風(fēng)扇消耗的功率。已知 Nl、Nh、πf、πc、πt，h、πt，l就可以進(jìn)行各流路的計算，隨時間推移便可完成動態(tài)仿真[5]。

2.2 動態(tài)數(shù)學(xué)模型和仿真設(shè)置

為了實現(xiàn)動態(tài)仿真，引入容積動力學(xué)模塊和轉(zhuǎn)子動力學(xué)模塊。其中通過容積動力學(xué)模塊可以計算得到Pt16、Pt4、Pt42、Pt7，從而得到 πf、πc、πt，h、πt，l；而通過轉(zhuǎn)子動力學(xué)模塊可以計算得到Nl、Nh。這樣就可以建立動態(tài)模型進(jìn)行動態(tài)仿真。

在simulink仿真前設(shè)置好參數(shù)和輸入、輸出方式：（1）設(shè)置仿真起始時間和終結(jié)時間分別為0和10；（2）設(shè)置算法仿真，選擇變步長龍格-庫塔連續(xù)算法，最小、最大步長和初始步長及誤差容限為默認(rèn)；（3）輸入和輸出設(shè)置，選擇從工作區(qū)導(dǎo)入（load from workspace），并將數(shù)據(jù)保存至工作區(qū)（save to workspace），限制輸出數(shù)據(jù)量為10000，其他參數(shù)為默認(rèn)[6]。

2.3 動態(tài)仿真

選擇相對成熟的GSP軟件中的1個模型作為參照，來驗證本文模型的準(zhǔn)確性。先設(shè)置動態(tài)仿真時的初始穩(wěn)態(tài)點和燃油變化量，在地面進(jìn)行發(fā)動機(jī)加、減速仿真。選擇典型的參數(shù)，如高、低壓轉(zhuǎn)速Nh、Nl和渦輪前溫度Tt4、發(fā)動機(jī)推力F作為比較量，進(jìn)行動態(tài)仿真，仿真結(jié)果如圖4所示。

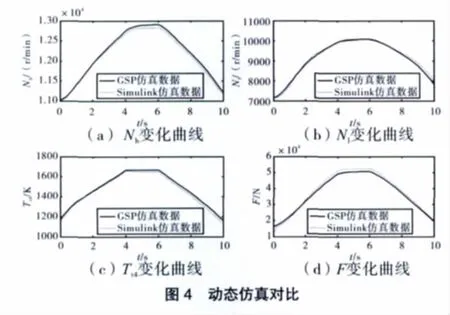
從圖4中可見，本文建立的發(fā)動機(jī)動態(tài)模型Simulink仿真的結(jié)果與GSP仿真的結(jié)果相近，除推力初始的個別數(shù)據(jù)誤差大于5%，其余數(shù)據(jù)的實際相對誤差均小于5%（如圖5所示）。

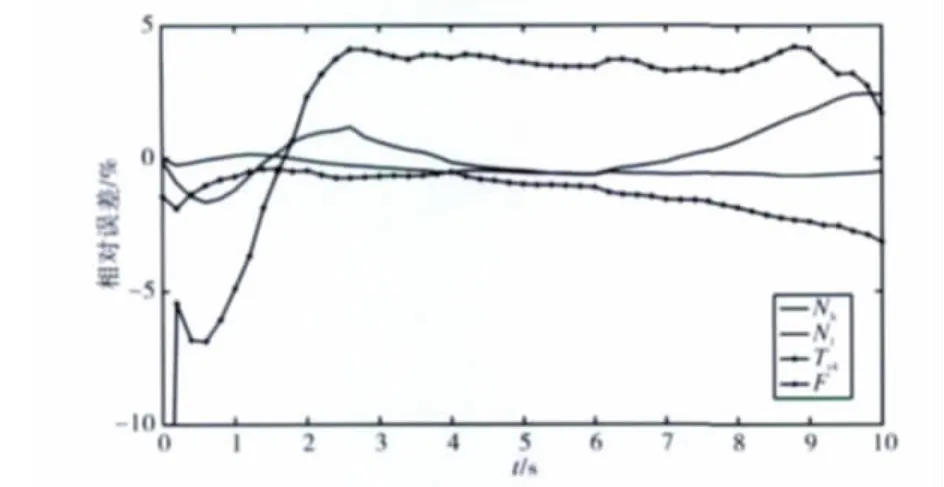
圖5 相對誤差分析

3 發(fā)動機(jī)穩(wěn)態(tài)仿真

發(fā)動機(jī)穩(wěn)態(tài)仿真是指發(fā)動機(jī)處于穩(wěn)定工作狀態(tài)，對各特征截面的物理參數(shù)求解。常規(guī)方法是使用Newton-Raphson方法對共同工作方程組進(jìn)行求解，此方法需反復(fù)運行雅可比矩陣，不僅運算量大，求解速度慢，而且對初值敏感，計算易發(fā)散[7]。本文對發(fā)動機(jī)穩(wěn)態(tài)仿真創(chuàng)新地采用基于發(fā)動機(jī)的動態(tài)仿真模型，以避免反復(fù)迭代過程，通過與GSP軟件穩(wěn)態(tài)仿真的結(jié)果對比，來驗證本方法的可行性和該模型的精度。

3.1 穩(wěn)態(tài)共同工作方程

上文中引入了4個容積動力學(xué)方程和2個轉(zhuǎn)子動力學(xué)方程，由于供油量隨時間的變化，不斷有變化的積分值輸出。而在發(fā)動機(jī)穩(wěn)態(tài)共同工作時，供油量為常值，流量滿足平衡，高、低壓轉(zhuǎn)子功率平衡，此時4個容積動力學(xué)模塊和2個轉(zhuǎn)子動力學(xué)模塊應(yīng)滿足

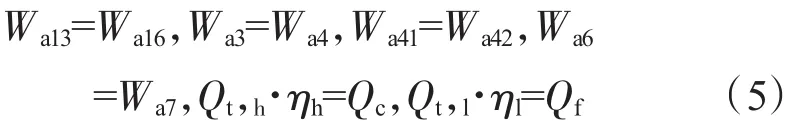
其中：Wa13=Wa21-Wa22，Wa4=Wa3+Wf≈Wa3（燃油量相對于Wa3可以忽略），Wa6=Wa5+Wa16，這樣就滿足了6個平衡方程，6 個未知數(shù) Nl、Nh、πf、πc、πt，h、πt，l就可以求得。在穩(wěn)態(tài)仿真開始時，4個容積動力學(xué)模塊和2個轉(zhuǎn)子動力學(xué)模塊還不滿足平衡條件，但隨著時間的推移，逐漸趨于平衡。其平衡時的數(shù)值即為穩(wěn)定工作時的數(shù)值。

3.2 穩(wěn)態(tài)仿真

在地面進(jìn)行發(fā)動機(jī)穩(wěn)態(tài)仿真，仿真結(jié)果如圖6所示。

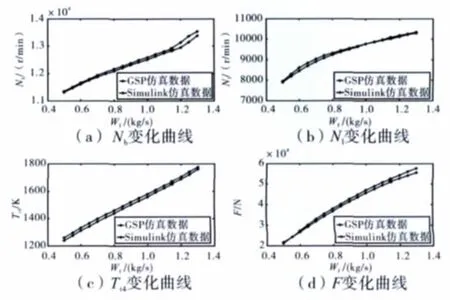
圖6 穩(wěn)態(tài)仿真對比

本文建立的發(fā)動機(jī)穩(wěn)態(tài)模型基于其動態(tài)模型，同樣取決于部件特性的準(zhǔn)確度和部件數(shù)學(xué)模型的準(zhǔn)確度。由圖5可知，其Simulink仿真的結(jié)果與GSP仿真的結(jié)果相近，實際相對誤差小于4%（如圖7所示）。

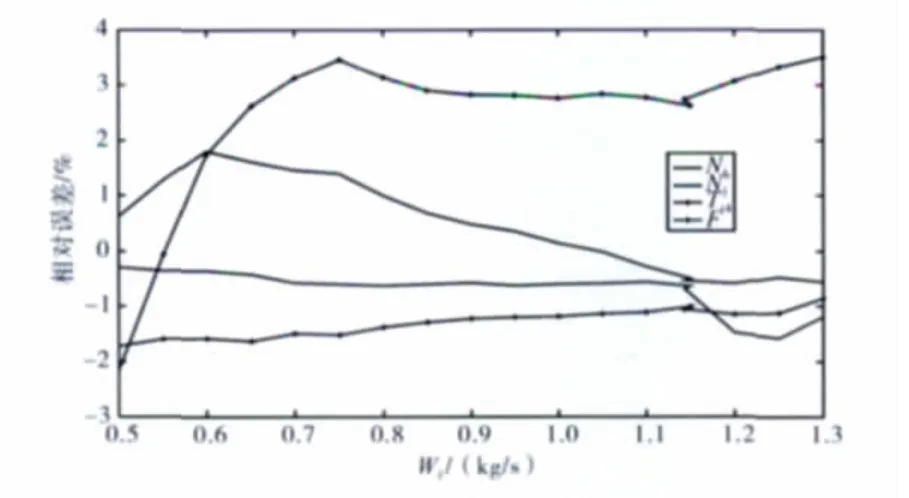
圖7 相對誤差分析

4 結(jié)論

（1）通過引入容積動力效應(yīng)，避免了反復(fù)迭代；在simulink中搭建了渦扇發(fā)動機(jī)的部件級模型，由已封裝的模型構(gòu)成了渦扇發(fā)動機(jī)專業(yè)模型庫，具有一定的通用性和擴(kuò)展性。

（2）對發(fā)動機(jī)進(jìn)行了動態(tài)和穩(wěn)態(tài)仿真，并與GSP仿真的結(jié)果進(jìn)行對比，可知該模型誤差較小，精度較高，具有良好的實時性，在航空發(fā)動機(jī)建模方法研究中具有一定參考價值。

[1]劉長福，鄧明.航空發(fā)動機(jī)結(jié)構(gòu)分析[M].西安：西北工業(yè)大學(xué)出版社,2006:18-29.

[2]韓曉光,曲文浩，董瑜，等.基于Simulink的燃?xì)廨啓C(jī)動態(tài)仿真模型[J].航空發(fā)動機(jī),2010,36（3）:20-25.

[3]Reed J A,Afieh A A.Computational simulation of gas turbines Part I-foundations of component-based models[J].Journal of Engineering for Gas Turbines Power,2000,122（3）：366-377.

[4]Evans A L,Follen G,Naiman C,et al.Numerical propulsion system simulation’s national cycle program[R].AIAA-98-3113.

[5]夏飛.基于MATLAB/SIMULINK的航空發(fā)動機(jī)建模與仿真研究[D].南京:南京航空航天大學(xué),2007.

[6]張志涌,楊祖櫻.MATLAB R2010a教程[M].北京:北京航空航天大學(xué)出版社,2010：252-266.

[7]季春生.航空發(fā)動機(jī)全數(shù)字仿真平臺設(shè)計[D].西安:西北工業(yè)大學(xué),2007.

[8]李家瑞.航空發(fā)動機(jī)建模技術(shù)研究[D].南京：南京航空航天大學(xué)，2005.

[9]樊思齊，李華聰.航空發(fā)動機(jī)控制：下冊[M].西安：西北工業(yè)大學(xué)出版社，2008：50-157.

[10]黃家驊，馮國泰.航空發(fā)動機(jī)特性仿真技術(shù)的進(jìn)展與展望[J].推進(jìn)技術(shù)，2002，23（4）：346-351.