總壓畸變對整機穩定性的影響研究分析

好畢斯嘎拉圖，周勝田，張志舒，胡 駿

（1.中航工業沈陽發動機設計研究所，沈陽 110015；2.南京航空航天大學能源與動力學院，南京 210016）

0 引言

先進航空發動機設計除具備高性能、高可靠性和良好隱身性之外，還必須滿足飛機適用性指標，在整個飛行包線范圍內具有足夠的可用穩定裕度，為此，在發動機設計過程中，需要對各種性能與可用穩定裕度等要求之間進行折衷，以達到最佳平衡。因此，對各類降穩因子對發動機穩定性的影響進行研究非常重要。大量研究表明，在各類降穩因子中，進氣畸變對發動機穩定性的影響最大[1]。

本文基于帶源項的2維非定常歐拉方程發展了1種預測進氣畸變對發動機穩定性和性能影響的數值計算方法，并分析總壓畸變對整機穩定性的影響。

1 計算方法

1.1 物理模型及網格劃分

在建立物理模型時，將一系列垂直于發動機軸線的截面劃分成若干個計算單元，且在圓周方向上將流道也劃分成一系列相同的扇形區，計算網格劃分如圖1所示。因此，每個計算單元是1個環形的通道扇形區(或子發動機)，其上、下邊界一般為內、外機匣，采用不可滲透的邊界條件。每個單元采用帶源項的非定常2維歐拉方程計算。發動機風扇/壓氣機部件可以整體作為1個單元，也可以分成幾個單元，每個單元可以是1級，也可以是若干級組。在計算中只需要給定每個單元進、出口截面的內外半徑、單元長度，及進口截面氣流角度和單元特性（如風扇壓氣機或高、低壓渦輪特性以及損失單元的流動損失特性等）。

1.2 數學模型

數學模型采用積分型的控制方程，坐標系為圓柱坐標系。本文主要計算周向畸變對發動機穩定性的影響，且根據俄羅斯穩定性理論認為徑向畸變對發動機穩定性的影響很小，可以忽略不計，在控制方程中忽略參數的徑向變化，而采用徑向平均參數。在模型中，以考慮黏性作用的各部件實際特性代表發動機各部件的氣動作用，將控制方程中的流動視為無黏流動，控制方程可簡化為帶源項的2維非定常無黏歐拉方程。

式中：C為氣流絕對速度；Cx、Cθ分別為氣流軸向和周向速度；ρ為氣流密度；g為引氣或放氣流量；S為截面面積；Sx、Sθ分別為軸向和周向面積；V 為體積；Fx、Fθ分別為軸向、周向葉片力和流道對氣流的軸向、周向作用力；Pn為相應截面面積上的總壓；Q為熱量；N為輪緣功；T為總溫；t為時間。

1.3 進、出口邊界條件

在發動機進口給定溫度和壓力的邊界條件，根據計算要求給定總壓或總溫(或二者的組合)與時間和周向坐標的關系

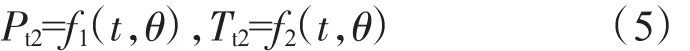
在出口邊界，即噴管臨界截面采用發動機的綜合節流特性

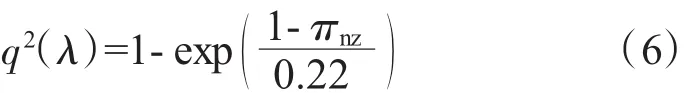
式中：πnz為噴管落壓比。

此外，設定噴管出口的壓力為環境靜壓。

1.4 控制方程求解

求解上述控制方程采用經典4階顯式Runge-Kutta格式時間推進法。

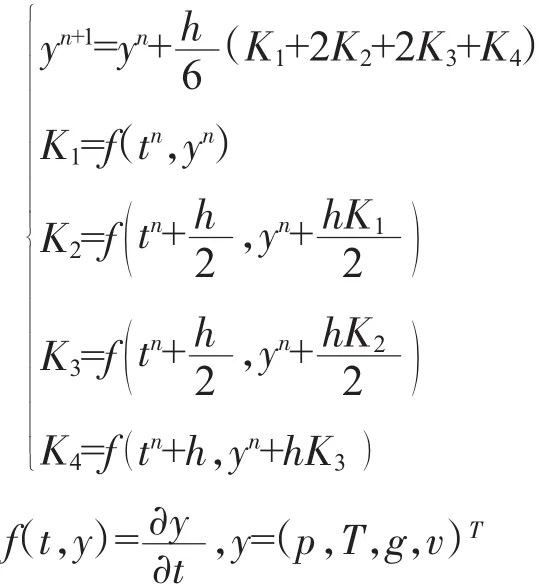
式中：h為時間步長；K為基本變量時間導數。

2 計算結果及分析

2.1 評定抗畸變能力

在計算中，采用穩態總壓畸變指數Δσ0/動態總壓畸變指數εav=1.272，畸變范圍為180°，畸變形式為方波。

總壓畸變敏感系數是指在給定轉速下的原始可用穩定裕度與在發動機上獲得的臨界綜合畸變指數之比，而臨界綜合畸變指數是指使風扇或壓氣機的穩定裕度降為零時的畸變指數。總壓畸變敏感系數為

式中：SMi為風扇/壓氣機試驗獲得的可用穩定裕度；Wcr為臨界畸變指數。

使用本模型預測的某型發動機典型狀態的總壓畸變，敏感系數見表1。

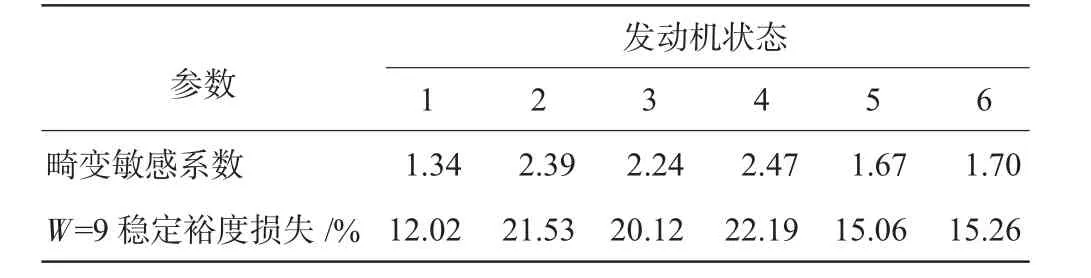
表1 在不同工作狀態下的發動機總壓畸變敏感系數

從表1中可見，狀態4的畸變敏感系數最大，抗畸變能力最差，對總壓畸變比較敏感，當發動機總壓畸變W=9時，穩定裕度損失為22.19%；當損失的穩定裕度大于發動機可用穩定裕度時，發動機就失去穩定工作能力，進入不穩定工作狀態。

2.2 總壓畸變對性能參數的影響

總壓畸變不僅對發動機穩定邊界有影響，還對發動機性能(如推力、耗油率等)有影響，如圖2、3所示。

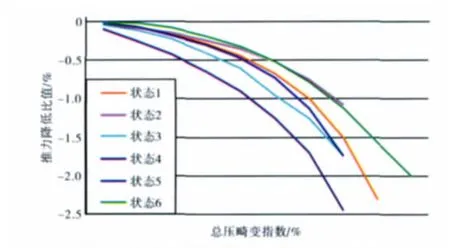
圖2 推力下降比值隨總壓畸變的變化

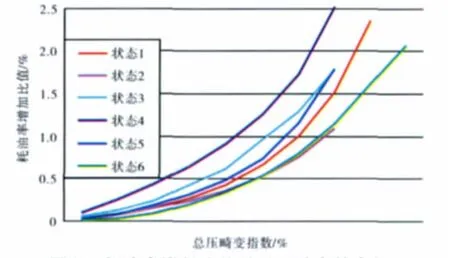
圖3 耗油率增長比值隨總壓畸變的變化

從圖2、3中可見，當燃燒室出口總溫不變時，總壓畸變指數的增大導致發動機推力減小和耗油率增加。如某型發動機在接近臨界總壓畸變情況時，其推力減小比值和耗油率增加比值均不到2.5%。由此可知，總壓畸變對發動機性能參數的影響比較小，特別是當畸變強度較小時，其對性能參數沒有明顯影響。由于在計算中忽略了總壓畸變對風扇/壓氣機特性的影響，可能會產生微小的計算誤差。

2.3 畸變軸向傳遞和衰減

在發動機工作過程中，進氣總壓畸變軸向傳遞使發動機各截面參數重新分布，進而影響發動機性能和穩定裕度。總壓畸變軸向傳遞如圖4所示。

圖4 在狀態3、W=9%畸變軸向傳遞

從圖4中可見，通過風扇時，總壓畸變大幅度衰減，同時生成大幅度的總溫畸變；通過壓氣機時，總壓畸變繼續衰減，并進一步生成總溫畸變。這種變化趨勢與實際情況比較吻合。通過燃燒室時，總溫畸變發生激烈變化，導致其被進一步放大。在不同工作狀態下，總壓畸變的變化如圖5、6所示。

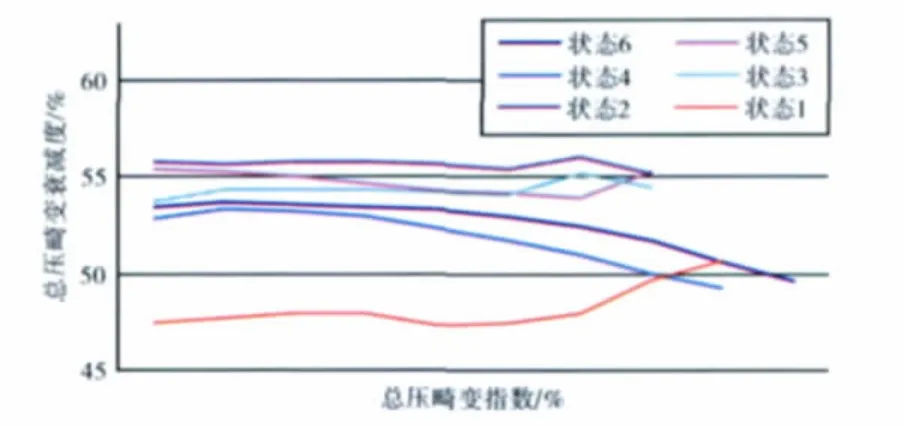
圖5 總壓畸變通過風扇時的衰減度

圖6 總壓畸變通過風扇時的總溫生成系數

從圖5、6中可見，在發動機所有典型工作狀態下，通過風扇時，總壓畸變的衰減程度都大于46%，總溫畸變生成系數都小于18%，并且隨著總壓畸變指數的增大，總壓畸變的衰減能力幾乎不變。總壓畸變通過風扇時衰減得越多，在壓氣機前面形成的組合畸變強度越小，壓氣機越不易失穩。

2.4 總壓畸變對發動機工作點的影響

總壓畸變雖然對將各子發動機參數平均后得到的整機性能影響不大，但是對各子發動機性能參數的影響比較大，即對各子發動機工作點的影響比較大，如圖7所示。

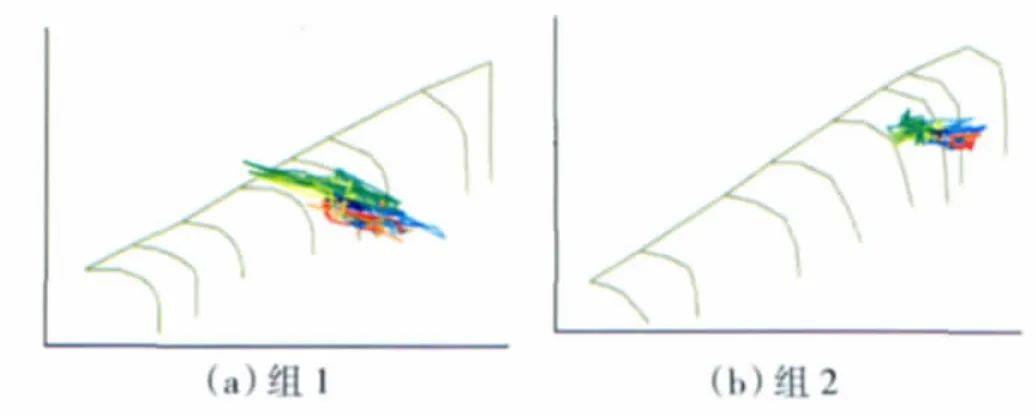
圖7 在狀態2、W=15%時風扇和壓氣機工作點的變化

從圖7中可見，在總壓畸變情況下，高、低壓區的子發動機工作點軌跡變化較大，而對將各子發動機參數平均后得到的整個發動機工作點軌跡變化較小，這與實際情況非常吻合。在同樣條件下，子發動機壓氣機工作點軌跡偏離初始狀態給定的等換算轉速線比較大。這主要是在計算中采用低壓轉子物理轉速不變，總壓畸變通過風扇時生成大幅度的總溫畸變而使低壓區的總溫增大，從而使相對換算轉速減小。

2.5 影響總壓臨界畸變指數的因素

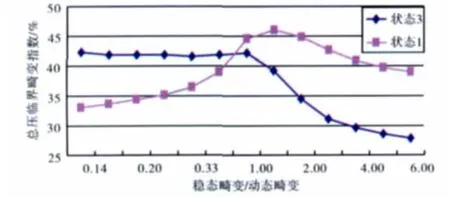
圖8 對臨界總壓畸變指數的影響

2.5.2 進口畸變形式對總壓敏感系數的影響

在相同的畸變范圍和工作狀態下，不同形式總壓畸變的畸變敏感系數不同。方波和準余弦波形式如圖9、10所示，其總壓畸變敏感系數對比結果見表2。

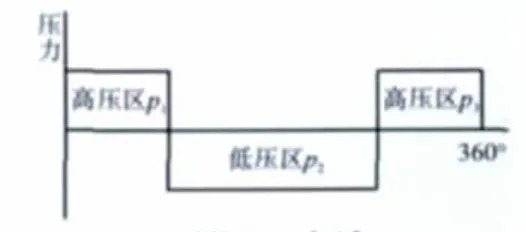
圖9 方波

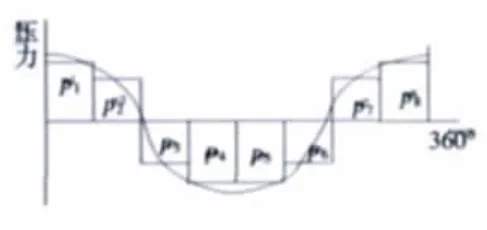
圖10 準余弦波

表2 敏感系數誤差對比

從表2中可見，在同一工作狀態、相同的畸變范圍和總壓畸變指數條件下，其準余弦波形式比方波形式小，且畸變敏感系數大，在狀態5條件下，其誤差達到了近6%。從而出現方波形式評定的敏感系數符合要求，而準余弦波形式的不符合要求。因此，用什么樣的畸變形式評定抗畸變能力還需進一步深入研究。

2.5.3 左支特性點對臨界總壓畸變指數的影響

左支特性如圖11所示。在圖中，S為喘振點，其左邊為左支特性，L是左支特性點；其右邊是右支特性，即風扇/壓氣機特性。在畸變條件下，雖然風扇/壓氣機部件局部葉柵通道經常出現失速團，但整個發動機仍具備穩定工作的能力。然而這種失速團若繼續擴大，是否會影響發動機穩定工作，與風扇/壓氣機左支特性點有很大關系。目前還無法通過試驗和計算準確得出風扇/壓氣機左支特性點對總壓臨界畸變指數的影響。本文把喘振點左下邊所有區域劃分成粗網格，并計算出每1個網格點值時的臨界總壓畸變指數。臨界總壓畸變指數值相應放大的結果如圖12所示。

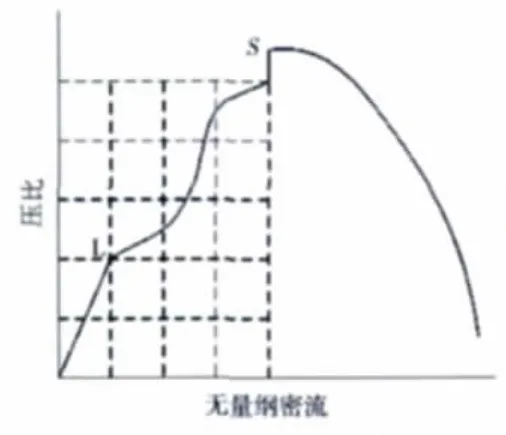
圖11 左支特性

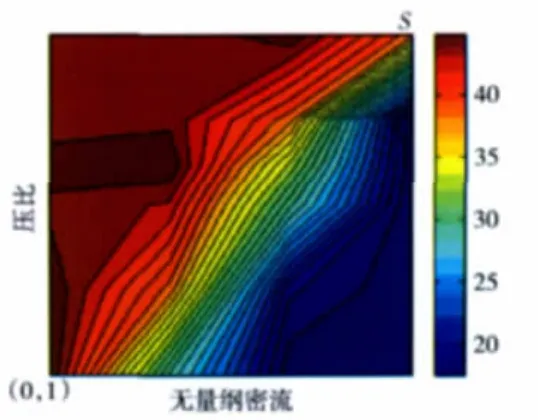
圖12 左支特性影響

從圖12中可見，左支特性點的選取影響臨界總壓畸變指數，影響程度主要與右支特性曲線接近喘振邊界時陡峭和平坦有關。右支特性曲線越陡峭，左支特性點對臨界總壓畸變指數的影響就越大；右支特性曲線越平坦，則其影響越小。總體上，左支特性點越往左上角取，相應的臨界總壓畸變指數就越大。

3 結論

（1）本文所建立的數學模型能很好地預測進氣畸變對發動機穩定性和性能的影響。

（2）總壓畸變對發動機穩定性的影響比較大，對發動機性能的影響比較小；計算得出某型發動機在狀態4時抗畸變能力最差。

（3）總壓畸變通過風扇大幅度衰減的同時生成較大的總溫畸變，并在壓氣機前形成組合畸變，使得壓氣機可用穩定裕度減小。

（4）臨界總壓畸變指數的主要影響因素為風扇/壓氣機左支特性、發動機進口總壓畸變形式和分配比例；評定發動機穩定性前需要與飛機協調確定評定發動機穩定性使用的畸變形式和分配比例。

[1]劉大響，葉培梁，胡駿，等.航空燃氣渦輪發動機穩定性設計與評定技術[M].北京：航空工業出版社，2004：14-72.

[2]廉筱純，吳虎.航空發動機原理[M].西安：西北工業大學出版社,2005：346-368.

[3]田寧，陳金國，張恩和.畸變對發動機穩定性的影響[J].航空發動機，2002（4）：25-28.

[4]王勤，劉世官，李承輝，等.發動機進氣總壓動態畸變流場測試及影響因素分析[J].航空發動機，2002（1）：6-11.

[5]William T C,Martin J G,Hooman R.Inlet distortion testingand analysis of a high-bypass ratio turbofan engine[R].ISABE-2003-1110.

[6]Mokelke H.The prediction of steady circumferential presure and temperature distortions in multistage axial compressor[J].Journal of Engineering for Power，1980，102：448-457.

[7]Amundson M H.Distortion test capabilities for future fighter aircraft engines[R].AIAA-89-2956.