改進的灰色模型在我國農村人均純收入預測中的應用

陳友余

（湖南財政經濟學院 工商管理系，湖南 長沙410205）

改進的灰色模型在我國農村人均純收入預測中的應用

陳友余

（湖南財政經濟學院 工商管理系，湖南 長沙410205）

以擴展我國農村人均純收入預測方法和提高預測精度為目標，采用變起點對傳統GM（1，1）模型進行改進，改進過程為建立一個預測模型群，改進結果為從預測模型群中挑選精度最高、擬合程度最好的模型作為預測模型，通過實際應用的確提高了預測精度和擬合程度，較大地增強了預測的可操作性和可信性。

GM（1，1）；變起點GM（1，1）；農村人均純收入

一、引言

農業是國民經濟基礎，農民問題是“三農”工作的重心。農村人均純收入呈現持續增長的同時,城鄉收入差距較大,影響和制約農民收入增長的因素仍然存在。基于此，本文依據2000～2010年農村人均純收入數據，運用改進的灰色模型對我國農村人均純收入進行預測。

灰色系統理論是鄧聚龍教授首次提出的，解決了學術界一直無人解決的微積分方程建模問題。其研究對象是“部分信息已知，部分信息未知”的小樣本、貧信息的不確定性系統，具有建模過程簡單，建模表達式簡潔等優點，被廣泛應用于經濟、生物、農業、醫藥、水利等領域，但其模型有一定的缺陷，不少學者對其進行了一定程度的改進，殘差GM（1，1）模型在實際應用廣泛。本文在傳統GM（1，1）模型的基礎上采用變起點方法進行改進，建立了一個預測群，從預測群中挑選最優的模型用于預測，這種方法一方面提高了預測精度和擬合程度，一方面增強了預測的可操作性和實用性。

二、傳統GM（1，1）模型

GM（1，1）模型是指，對原始時間序列進行一次累加，從而生成的序列具有強遞增特性，然后建立相應的近似微分方程，來體現序列的發展規律。其方法如下：

（一）原始時間序列 x（0）=（x（0）（1），x（0）（2），…，x（0）（n）），其中n為原始數據個數，對x（0）進行一次累加生成序列x（1），即IAGO，得：x（1）=（x（1）（1），x（1）（2），…，x（1）（n）），其中（i），其中i=1，2，…，n（以下不做特殊說明，i的取值與此相同）。

（二）檢驗x（0）的準光滑性和x（1）的準指數規律。準光滑系數時一般認為滿足準光滑條件；準指數規律指標一般認為滿足準指數規律。

（三）若p（i+1）<0.5，σ（1）（i）綴[1，1.5]，則GM（1，1）的白化微分方程為其中，-a為發展灰度，b為灰色作用量，a、b均為待定系數；t表示時間；由于x（1）（i）與灰導數不滿足平射關系，本文采用傳統方法對序列x（1）采用緊鄰均值生成序列 w（1），即w（1）=（w（1）（1），w（1）（2），…，w（1）（n）），其中w（1）（i+1）=0.5x（1）（i）+0.5x（1）（i+1）。于是白化微分方程對應的灰微分方程為：x（0）（i）+aw（1）（i）=b.

于是x（0）（i）+aw（1）（i）=b可等價變形為：Y=BA，對于兩個未知系數（a與b）的n-1個方程是無解的，此時考慮利用最小二乘法近似得到A贊=（BTB）-1BTY，可求出近似解a贊，b贊。

（五）將a贊，b贊代入灰微分方程，求得離散響應函數：

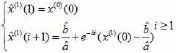
（六）對x贊（1）（i+1）進行累減還原，得到原始數據的預測值：

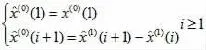
（七）精度檢驗

（八）擬合度檢驗

灰色關聯分析是通過確定原始序列和預測序列的幾何形狀的相似程度來判斷其緊密程度，從而對原始序列動態發展態勢進行量化比較分析。其步驟是將預測序列與原始序列進行無量綱化處理，計算關聯系數和關聯度，再根據關聯度的大小判定緊密程度。

第1步，變量的無量綱化，求原始序列與預測序列的初值像（或均值像），本文選用初值像；

ρ為分辨系數，ρ越小，分辨力越大，當ρ燮0.5463時，分辨力最好，通常取ρ=0.5，本文也取ρ=0.5。

三、變起點GM（1，1）模型

在實際預測建模中，不一定用原始序列中全部的數據來建模。在原始序列中有規律挑選一部分數據 （數據至少為4個），就可建立一個模型。為了提高傳統GM（1，1）模型的預測精度和擬合程度，建模數據中應為包含x（0）在內的一個等時距序列，基于這種思想，以x（0）為建模取值的終點，從后往前不斷取值，可以建立一個預測模型群，從預測模型群中挑選最優的模型用于以后的預測，其建模和求解如下：

1.給定原始時間序列x（0）=（x（0）（1），x（0）（2），…，x（0）（n）），其中n為原始數據個數；

2.用x（0）=（x（0）（1），x（0）（2），…，x（0）（n））建立的GM（1，1）模型為全部數據模型；用x（0）=（x（0）（i），x（0）（i+1），…,x（0）（n））（i叟2）建立的GM（1，1）模型為部分數據模型；

3.由于最短時間序列中數據至少為4個，于是可建立一個4維子序列：（x（0）（n-3），x（0）（n-2），x（0）（n-1），x（0）（n）），依次往下，最后可建立一個n維子序列（即原時間序列），總共可建立n-3個子序列；

4.對各子序列按傳統GM（1，1）模型方法進行預測，并進行精度檢驗和擬合度檢驗，從模型群中挑選最優的模型應用于預測。

四、改進的灰色模型在我國農村人均純收入預測中的應用

21世紀開局以來，我國農村人均純收入見下表，數據均來至于《全國國民經濟和社會發展統計公報》。

表1 ：我國2000~2010年農村人均純收入（單位：元）

（一）構建傳統GM（1，1）模型

首先建立我國農村人均純收入序列，同時對x（0）進行一次累加生成序列x（1），即I-AGO，計算過程在此不贅述；然后檢驗x（0）的準光滑性和x（1）的準指數規律。當i＞2時，p（i）<0.5，σ（1）（i）綴[1，1.5]，滿足準光滑性和準指數規律要求，構造矩陣B和常數矩陣Y；再應用Excel中的LINEST可求出a贊=-0.1107，b贊= 1773.23； 將a贊，b贊代灰微分方程， 求得離散響應函數，在此基礎上，對進行累減還原，得到原始數據的預測值，最后進行精度檢驗，通，s1=過計算，平均相對誤差，可見可見后驗差比值c<0.35，小誤差頻率P=1，關聯度為0.6366，可見預測誤差的一般水平很低，預測誤差擺動的幅度小，誤差較小的概率達到了100%，可知精度高，能達到擬合要求。可見，我國2000~2010年農村人均純收入序列能完全通過檢驗，可用于預測。

（二）變起點GM（1，1）模型

1.由于n=11,故可建立8個子序列。

2.對各子序列按傳統GM（1，1）模型方法進行預測，得各模型對應的離散響應函數；通過計算平均相對誤差、后驗差比值和小誤差頻率和灰關聯度，對各子模型進行精度比較和擬合程度比較：平均相對誤差方面，11維子序列達到1級精度，5維子序列達到3級精度，其余子序列達到2級精度，2級精度由高到低順序為：4維子序列最高，6維子序列，8維子序列和9維子序列次之，然后是10維子序列，最后是7維子序列；后驗差比值方面，各子序列均達到了1級精度，精度由高到低順序為：9維子序列，8維子序列，10維子序列，6維子序列，5維子序列，11維子序列，4維子序列，7維子序列；小誤差頻率方面，各子序列均達到了1級精度；擬合度檢驗方面，15維子序列及4維子序列擬合程度不滿意，其余均滿意，滿足條件的子序列擬合程度由高到低順序為：8維子序列，7維子序列，10維子序列,11維子序列，9維子序列，6維子序列和8維子序列，綜合以上比較，選擇8維子序列作為預測模型。

五、結論

本文先用傳統GM（1，1）模型對我國農村人均純收入進行預測，然后采用變起點對傳統GM（1，1）模型進行改進，建立一個預測模型群，從預測模型群中結合精度要求和擬合程度要求挑選了最優的8維子序列作為預測模型，這種方法既提高了預測精度和擬合程度，又增強了預測的可操作性和實用性。

[1]鄧聚龍.灰色系統理論的GM模型[J].模糊數學，1985，（2）：23-32.

[2]王宇熹，汪泓，肖峻.基于灰色GM（1，1）模型的上海城鎮養老保險人口分布預測[J].系統工程理論與實踐，2010，30（12）：2244-2253.

[3]張勇軍，袁德富.電力系統可靠性原始參數的優化GM（1，1）預測[J].華南理工大學學報（自然科學版），2009，37（11）：50-55.

[4]崔冬冬，陳建康，吳震宇，程黎明.大壩變形度的不等維加權動態GM（1，1）預測模型[J].長江科學院院報，2011，28（6）：5-9.