弱各向異性下晶體生長的相場模型模擬

趙達文

（太原科技大學材料學院，山西太原 030024）

凝固是典型的一級相變過程。在純物質的凝固過程中，首先通過起伏形成晶核，其后沿著各個方向生長從而形成各種凝固組織。理論分析表明[1，2]，這些生長方向與液固界面上的各向異性密切相關。各向異性是指液固界面的一些物理性質是晶向的函數，常見的有界面能各向異性和動力學各向異性。當各向異性效應較顯著時，晶體沿著各向異性決定的方向以枝晶方式生長。在無、弱各向異性條件下不存在優勢生長方向，因此各個晶向上都以相同速度生長，當界面曲率半徑超過臨界值后，會在擾動的作用下發生失穩現象[3]。弱各向異性條件下界面形態演化以及生長方式等都是凝固學的重要內容。對于顯著各向異性條件下生長行為已有眾多研究報道，而對弱各向異性下生長缺乏相應的研究。

由于數學上的困難，凝固理論無法預測弱各向異性下界面形態演化過程；同時，由于界面各向異性值很難精確測量、各向異性值無法自由調整等原因，導致實驗研究也存在較大困難，所以通常用數值模擬方法進行研究。相場模型通過引入序參量場從而避免了顯式追蹤界面的困難，在凝固組織模擬中得到了廣泛應用[5，6]。

本文以自適應有限元方法求解相場模型，分別對界面能和動力學弱各向異性條件下的晶體生長過程進行模擬，從而對其生長規律進行深入研究。

1 相場模型

這里采用Karma等提出的純物質凝固相場模型[4]。該模型優點是數值求解時保證精度的前提下可以采用較大的界面厚度，并且所引入的網格各向異性遠小于傳統相場模型。其控制方程由序參量方程和溫度場控制方程組成：

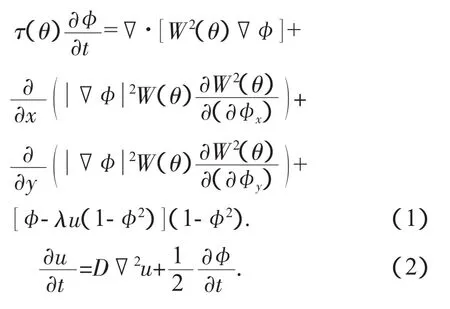
式中：為序參量；u≡（T-Tm）/（L/cp）是無量綱溫度；T是熱力學溫度；Tm是熔點；L是結晶潛熱；cp是等壓熱容；D代表熱擴散系數；λ代表耦合常數；θ為界面法線與x軸夾角。τ（θ）為原子弛豫時間，W（θ）為彌散界面厚度，二者分別對應界面能和動力學效應，在不同各向異性條件下有不同形式，具體形式見模擬結果部分。

2 求解方法與計算參數

采用自適應有限元方法求解相場模型，使用自適應網格可以在計算精度不變前提下使求解計算量降低一階。在空間域上采用伽遼金加權余量法對方程（1）、（2）進行離散，在時間域上分別采用向前差分和C-N格式對二者進行離散，采用ICCG方法求解線性方程。

計算中所采用矩形單元會引入額外的網格各向異性，當各向異性值較弱時，網格各向異性的影響必須予以考慮。計算中采用如下措施來降低網格各向異性影響[5～7]：1）采用薄界面漸近的相場模型；2）采用較小的空間步長；3）通過計算各種參數下的網格各向異性，對所輸入各向異性值進行校準。

3 模擬結果與討論

如上所述，液固界面上常見各向異性有界面能和動力學各向異性。在相場模型中，二者分別體現在界面厚度W（θ）和原子的弛豫時間τ（θ）上。本節中分別對弱界面能、動力學各向異性作用下的晶體生長進行模擬。計算中用到的參數為W0=1.0，τ0=1.0，D=1.0，d0/W0=0.577，△x/W0=0.4，△t/τ0=0.008，無量綱過冷度△=0.65。計算區域大小為409.6W0×409.6W0，初始晶核半徑R0=10，計算區域邊界為絕熱邊界條件。

3.1 弱動力學各向異性控制下晶體生長

界面動力學是指液相原子穿過界面最終吸附在固相的過程，在此過程中消耗的驅動力即為動力學過冷。這里設定界面厚度W（θ）各向同性、弛豫時間τ（θ）具有四重對稱性

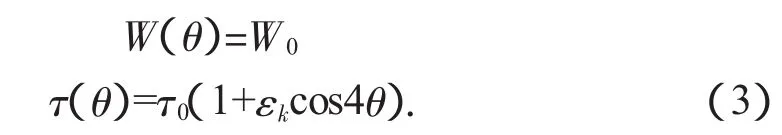
來模擬界面動力學各向異性作用下的生長過程，其中耦合系數λ=5.77.

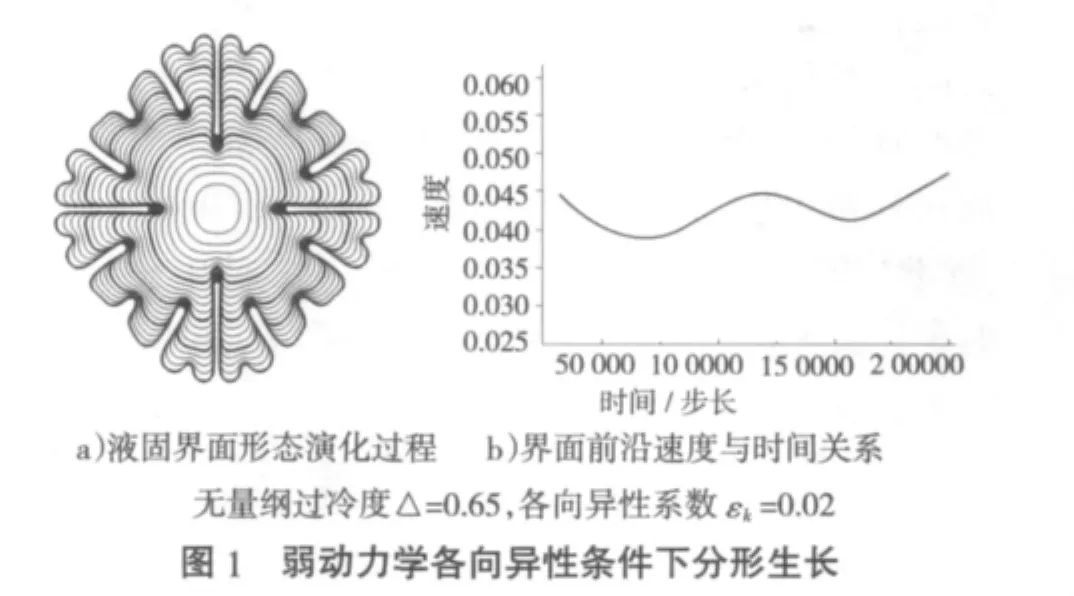
模擬結果表明，當動力學各向異性εk≤0.02時，固相不再以枝晶方式生長。圖1a）為εk=0.02時的液固界面形態演變過程，圖中輪廓線為間隔1萬時間步長的液固界面；圖1b）為x軸方向界面前沿的生長速度曲線。在7萬步左右時，界面前沿的曲率半徑達到極大值，在M-S不穩定性的調制下，界面開始發生分叉（最內側粗實線）；此時界面生長速度位于第一個波谷位置。緊接著產生分叉。在12萬步左右，界面分叉過程已經完成，此時界面前沿的曲率半徑達到極小值（圖1a）次內側粗實線）；而V達到第一個波峰位置的極大值。隨著生長過程的進行，在16萬步左右界面曲率半徑再次達到極大值（圖1a）中次外側粗實線），開始第二次分叉過程；此時生長速度V為極小值（圖1b）中的第二個波谷位置）。在21萬步左右，第二次分叉過程完成，界面曲率半徑再次取極小值（圖1a）外側粗實線），生長速度到達圖1b）中的第二個波峰位置。可見，隨著時間的推移生長前沿重復性的發生分叉現象，生長速度隨時間的推移而波動。

3.2 弱各向異性界面能控制下晶體生長

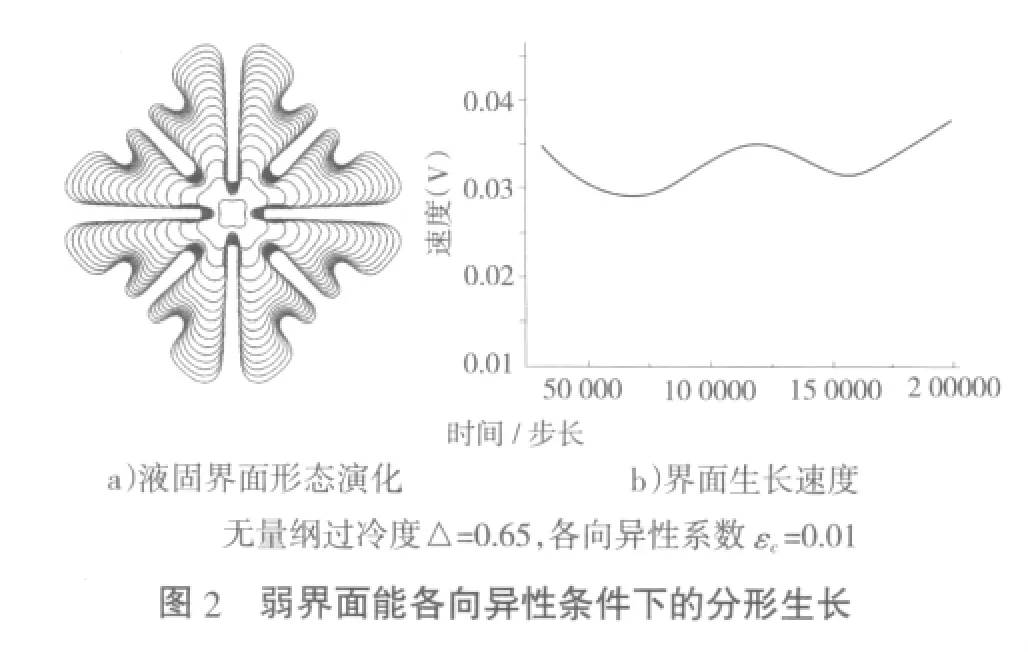
為了單獨考察界面能各向異性的影響，這里設定W（θ）=W0（1+εccos4θ），τ（θ）=τ0（1+εccos4θ）2，并通過選擇耦合常數λ來消除界面動力學效應。當界面能各向異性系數εc取≥0.02時，固相以枝晶方式生長；而當值εc取0.00001時，晶體不再以枝晶方式生長。圖2a）是εc=0.01液固界面演化過程，圖中相鄰界面時間間隔為1萬步；圖2b）為x軸附近界面前沿的生長速度。在生長過程中界面前沿周期性的發生分叉，相應的生長速度持續性的波動，同樣不存在穩定生長狀態。

綜合以上模擬結果，可以發現在弱各向異性下具有相同的生長方式：界面前沿總是持續性分叉、生長速度周期性波動、不存在與枝晶生長類似的穩定生長狀態。究其原因，是由于在生長過程中由于不存在優勢生長方向，使得界面每個位置以相近或相同的速度向各個方向生長；當界面前沿曲率半徑大于臨界半徑值時，在M-S不穩定性的調制下界面失穩發生分叉[3]；當前沿的曲率半徑再度超過臨界半徑時，生長前沿再次發生分叉。通常將這種生長方式稱之為分形生長[8]。注意分形生長與有限空間內的doublon生長模式不同[9]，雖然二者的生長形態類似，但是分形生長不存在穩定生長形態和生長速度，而doublon存在穩定生長狀態。

4 結 論

使用相場模型對弱各向異性條件下晶體生長進行了模擬。模擬結果表明，在各向異性較弱時固相均以分形方式生長。由于不存在優勢生長方向，生長過程中界面前沿總是持續的發生分叉、生長速度周期性的波動，不存在類似枝晶穩態生長的生長狀態。

［1］Langer J S，Hong D C.Solvability Conditions for Dendritic Growth in the Boundary-Layer Model with Capillary Anisotropy［J］.Phys Rev A，1986，34（2）：1462-1471.

［2］Langer J S.Recent Developments in the Theory of Pattern-Formation［J］.Physica A，1986，140（1-2）：44-50.

［3］Mullins WW，Sekerka R F.Morphological Stability of a Particle Growing By Diffusion of Heat Flow ［J］.J Appl Phys，1963，34：323-329.

［4］Karma A，Rappel W J.Quantitative phase-field modeling of dendritic growth in two and three dimensions ［J］.Phys Rev E，1998，57：4323-4349.

［5］趙達文.過冷熔體凝固的相場法自適應有限元模擬［D］.西安：西北工業大學，2006.

［6］趙達文，李金富.相場法模擬動力學各向異性對過冷熔體中晶體生長的影響［J］.金屬學報，2009，45（10）：1237-1241.

［7］趙達文.自適應有限元方法凝固問題模擬的網格各向異性研究［J］.鑄造設備與工藝，2011（2）：20-22.

［8］Johnson B K，SekerkaR F，Foley M P.Scaling of Fractal Aggregates［J］.Phys Rev E.1995，52（1）：796-800.

［9］Brener E，Müller-Krumbhaar H，Saito Y，et al.Crystal-Growth in a Channel-Numerical Study of the One-Sided Model［J］.Phys Rev E，1993，47（2）：1151-1155.