中國(guó)期貨市場(chǎng)非交易時(shí)段的VaR與ES測(cè)度研究

張 舒，仲偉俊，梅姝娥

（東南大學(xué) 經(jīng)濟(jì)管理學(xué)院，江蘇 南京210096）

一、引 言

近年來，隨著金融市場(chǎng)一體化程度的不斷加深、期貨交易時(shí)間的延長(zhǎng)、在開盤之前和收盤之后的信息發(fā)布等大量事件的發(fā)生，某種程度上已改變了非交易期間可得的財(cái)經(jīng)信息數(shù)量及其重要性。目前，我國(guó)的商品期貨均在白天交易，總交易時(shí)間尚不到非交易時(shí)段的一半。然而，很多價(jià)格敏感的國(guó)內(nèi)外金融信息其實(shí)是在相對(duì)冗長(zhǎng)的非交易期間發(fā)布的，如依據(jù)前一天收盤后發(fā)布的當(dāng)?shù)鼗蛉蛐哉吖娴取＿@些信息都可能反映在開盤和收盤時(shí)的價(jià)格之中，從而加大期貨市場(chǎng)風(fēng)險(xiǎn)。并且，非交易時(shí)間的長(zhǎng)度不同，也使得平均積累的信息總量有所差異。根據(jù)時(shí)間的長(zhǎng)短，我們將非交易時(shí)段劃分為交易當(dāng)晚、短期假日、周末假日和中長(zhǎng)假日四種［1，2］。并且，Taylor、Tsiakas［1，2］認(rèn)為，在期貨交易及其風(fēng)險(xiǎn)管理中，非交易的金融信息扮演著非常重要的角色，不僅能夠?yàn)槠谪浭袌?chǎng)的價(jià)格發(fā)現(xiàn)提供預(yù)測(cè)，還可為風(fēng)險(xiǎn)管理中的風(fēng)險(xiǎn)測(cè)度提供必要的信息支持。因此，我們只有對(duì)非交易時(shí)段的市場(chǎng)風(fēng)險(xiǎn)進(jìn)行清晰的認(rèn)識(shí)與測(cè)度，才能利用有價(jià)值的金融信息對(duì)期貨市場(chǎng)進(jìn)行有效利用和管理。

二、文獻(xiàn)綜述

風(fēng)險(xiǎn)價(jià)值（Value at Risk，VaR）方法被用來度量和管理損失，其最早來自Baumol［3］在管理科學(xué)領(lǐng)域的應(yīng)用。在20世紀(jì)90年代，J P Morgan建立了用來度量資產(chǎn)市場(chǎng)損失的一種經(jīng)典的風(fēng)險(xiǎn)價(jià)值法，其經(jīng)濟(jì)學(xué)意義是指在給定置信度水平下，某一金融資產(chǎn)或證券組合在未來特定的一段時(shí)間內(nèi)所遭受的最大可能損失。VaR現(xiàn)已發(fā)展成為現(xiàn)代風(fēng)險(xiǎn)管理的國(guó)際標(biāo)準(zhǔn)和理論基礎(chǔ)。VaR之所以迅速在各國(guó)金融機(jī)構(gòu)廣泛應(yīng)用，很大程度上是因?yàn)樗敲枋鼋o定組合可能遭受損失大小的一種方法，且具有靈活性，能夠滿足各種金融機(jī)構(gòu)的需要。但是VaR本身也存在一些局限，對(duì)VaR方法的批評(píng)主要在于其不滿足一致性，尤其是次可加性［4］。另外，VaR只能度量正常情況下的最大損失，對(duì)于因?yàn)轱L(fēng)險(xiǎn)因子波動(dòng)產(chǎn)生的極端情況，并不能有效度量。VaR方法的不足之一來源于概念或是理論上的局限性，不足之二是它需要對(duì)金融市場(chǎng)的趨勢(shì)做理論上的假定，如分布的正態(tài)性等問題。為彌補(bǔ)這些不足，Engle和 Manganel［5］于1999年提出了預(yù)期損失（Expected Shortfall，ES）的概念。ES值是損失超過VaR的條件均值，反映了超額損失的平均水平。一些學(xué)者［6-8］已經(jīng)證明，計(jì)算厚尾數(shù)據(jù)（非正態(tài)分布）時(shí)，使用ES模型來測(cè)度風(fēng)險(xiǎn)，會(huì)得到更好的估計(jì)效果。且ES方法可以用作度量超過VaR的損失，滿足并符合由Artzner在1997年提出的一致性公理［9］。由此，結(jié)合 VaR和ES的雙風(fēng)險(xiǎn)門限的監(jiān)管將對(duì)企業(yè)和金融機(jī)構(gòu)提供更加合理、有效的風(fēng)險(xiǎn)度量標(biāo)準(zhǔn)，目前這一方法正日益受到各方重視。

在VaR的計(jì)算中，最關(guān)鍵的是對(duì)資產(chǎn)價(jià)格變化的累計(jì)分布函數(shù)進(jìn)行假設(shè)，計(jì)算分布函數(shù)的現(xiàn)有方法主要有：風(fēng)險(xiǎn)矩（Riskmetrics）法、GARCH法、分位數(shù)法和極值理論（Extreme Value Theory，EVT）［10］。風(fēng)險(xiǎn)矩法是假設(shè)資產(chǎn)組合的日連續(xù)復(fù)利收益服從條件正態(tài)分布；GARCH法主要是利用條件異方差模型進(jìn)行分析，針對(duì)模型中誤差項(xiàng)分布的不同假設(shè)又分為基于高斯分布、學(xué)生t分布和廣義誤差分布的GARCH模型等；分位數(shù)法是估計(jì)VaR的一種非參數(shù)法，它不需要對(duì)資產(chǎn)的收益進(jìn)行假設(shè)，目前主要分為兩類：經(jīng)驗(yàn)法和分位數(shù)回歸法；極值理論主要對(duì)極端市場(chǎng)情況下的風(fēng)險(xiǎn)損失進(jìn)行估計(jì)，可以準(zhǔn)確地描述分布尾部的分位數(shù)。使用極值理論來建立VaR管理機(jī)制的背景主要在于一般權(quán)益市場(chǎng)（或其它金融機(jī)構(gòu)）大都使用簡(jiǎn)化的VaR風(fēng)險(xiǎn)管理制度（俗稱的σ-based的VaR），這些簡(jiǎn)化的VaR制度是在正態(tài)分布的假設(shè)下運(yùn)行的，當(dāng)風(fēng)險(xiǎn)事件發(fā)生時(shí)，概率分布將偏離正態(tài)性，從而出現(xiàn)厚尾極值現(xiàn)象［11］。此時(shí)，簡(jiǎn)化的VaR將出現(xiàn)嚴(yán)重偏誤，而基于極值理論的VaR則可有效避免這些偏誤。由于絕大多數(shù)金融時(shí)間序列是非對(duì)稱的，在計(jì)算VaR的各種方法中，極值理論方法將比傳統(tǒng)方法更適合于對(duì)厚尾極端分位點(diǎn)的預(yù)測(cè)。

近年來，國(guó)內(nèi)學(xué)者在期貨市場(chǎng)風(fēng)險(xiǎn)價(jià)值中的應(yīng)用方面進(jìn)行了一系列研究，取得了不少有價(jià)值的成果。遲國(guó)泰等［12］借助多元 GARCH（1，1）模型所預(yù)測(cè)的多種期貨組合的協(xié)方差矩陣，計(jì)算了該期貨組合的波動(dòng)值，并結(jié)合風(fēng)險(xiǎn)價(jià)值建立了基于多元GARCH-VaR的多種期貨合約組合市場(chǎng)風(fēng)險(xiǎn)評(píng)價(jià)模型。韓德宗［13］以鄭州商品交易所的硬麥期貨和上海期貨交易所的銅期貨為例，計(jì)算了收益的VaR值，對(duì)預(yù)測(cè)結(jié)果的有效性進(jìn)行了檢驗(yàn)。劉慶富等［14］利用基于廣義誤差分布的 VaR-GARCH（1，1）模型對(duì)我國(guó)期貨市場(chǎng)風(fēng)險(xiǎn)進(jìn)行了測(cè)度。雖然如此，當(dāng)前對(duì)期貨市場(chǎng)的風(fēng)險(xiǎn)測(cè)度主要集中于傳統(tǒng)收益的風(fēng)險(xiǎn)測(cè)度上，而對(duì)我國(guó)期貨市場(chǎng)非交易風(fēng)險(xiǎn)的測(cè)度尚未涉及。為此，本文將試圖利用基于極值理論的VaR和ES模型對(duì)這一問題進(jìn)行探索。

三、非交易收益與風(fēng)險(xiǎn)測(cè)度模型

為計(jì)算期貨市場(chǎng)的非交易風(fēng)險(xiǎn)，下文首先給出非交易收益的測(cè)度公式，在此基礎(chǔ)上，分別給出基于極值理論的風(fēng)險(xiǎn)測(cè)度模型。

（一）非交易收益的測(cè)度公式

根據(jù)前文非交易時(shí)段假日的分類，借鑒Tsiakas［2］界定股票市場(chǎng)非交易收益的思想，下文具體給出期貨市場(chǎng)非交易收益的數(shù)據(jù)生成過程。用Pct表示t日收盤價(jià)格，表示t日開盤價(jià)格。那么，每日收益rt、日間交易收益和非交易收益可分別表示為：

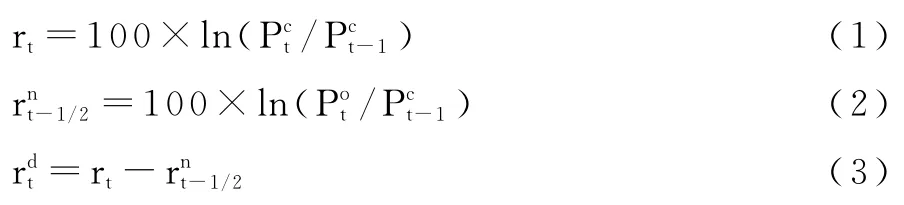
定義每日收益時(shí)，時(shí)間為整數(shù)，而非交易收益定義為整數(shù)時(shí)間的一半。根據(jù)這一標(biāo)準(zhǔn)，我們把非交易期間按照時(shí)間長(zhǎng)度劃分為四類互不重疊的非交易收益：（1）為周一至周四交易當(dāng)晚的收益，測(cè)度的是前一日收盤到當(dāng)日開盤這一時(shí)段的收益；（2）為短期假日的收益，測(cè)度的是當(dāng)日下午收盤到隔日開盤這一時(shí)段的收益；（3）為周末假日的收益，測(cè)度的是周五收盤至周一開盤這一時(shí)段的收益；（4）為中長(zhǎng)假日的收益，測(cè)度的是假日在周一或周五時(shí)，假日前收盤到假日后開盤這一時(shí)段的收益。短期假日、周末假日和中長(zhǎng)假日分別比交易當(dāng)晚至少長(zhǎng)24小時(shí)、48小時(shí)和72小時(shí)［23］。

（二）基于EVT的風(fēng)險(xiǎn)測(cè)度模型

1.VaR與ES模型的建立

極值理論是度量市場(chǎng)風(fēng)險(xiǎn)極端情形的一種方法，它具有超越樣本數(shù)據(jù)的估計(jì)能力，并可以準(zhǔn)確地描述分布尾部的分位數(shù)，利用它來計(jì)算的VaR和ES可以實(shí)現(xiàn)更高的精確度。極值理論主要包括兩類模型，即傳統(tǒng)的分塊樣本極值模型和近年來發(fā)展起來的POT（Peaks Over Threshold）模型。分塊樣本極值模型是對(duì)大量同分布樣本分塊后的極值進(jìn)行建模，所以需要采用大量的數(shù)據(jù)，實(shí)際中往往不能滿足這一條件。POT模型則是對(duì)樣本數(shù)據(jù)中超過某一充分大閾值的所有樣本數(shù)據(jù)進(jìn)行建模，即只是考慮對(duì)尾部的近似表達(dá)，而不需要對(duì)整個(gè)分布進(jìn)行建模，這就克服了其他度量方法在解決厚尾分布上的缺陷，可以對(duì)損失分布直接進(jìn)行數(shù)理分析。并且POT模型使VaR和ES值的計(jì)算更為簡(jiǎn)便。其中，廣義帕累托分布（General Pareto Distribution，GPD）是廣泛應(yīng)用的一種POT模型。

設(shè)隨機(jī)變量X服從分布函數(shù)F，VaR被定義為在給定置信水平q下未來一定時(shí)間內(nèi)期貨收益所遭受的最大可能損失，即 VaRq＝F-1（1-q）（F-1為分位數(shù)函數(shù)）［9，15，16］。若置信水平q給定，我們可得到VaR的測(cè)度公式：

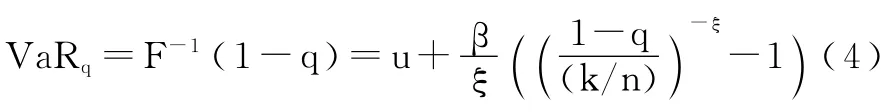
以VaR為基礎(chǔ)，可以計(jì)算超過VaRa的預(yù)期損失 ES［15］，其計(jì)算公式為：

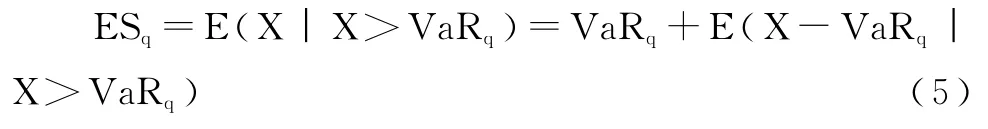
其中，E（X-VaRq︱X＞VaRq）為給定閾值 VaRq時(shí)的均值超越函數(shù)（Mean Excess Function）。當(dāng)ξ＜1時(shí)，我們有：

由等式（5）和（6）可以求出ES的表達(dá)式：

其中，u為時(shí)間序列的閾值，ξ為分布的形狀參數(shù)，β為與閾值u有關(guān)的尺度參數(shù)。

2.超越閾值分布的選擇

POT方法關(guān)注超過某一閾值的分布狀況。為此，我們?cè)O(shè)每日收益變化的隨機(jī)變量Xi（i＝1，…，n）是獨(dú)立同分布的，它們的共同分布為F（x）＝Pr（Xi≤x）。選取一個(gè)閾值u，使得u小于F支撐集的右端點(diǎn)，即u＜ω（F）＝sup｛x∶F（x）＜1｝。我們記X為任意的Xi（i＝1，…，n）并定義超越閾值u的超額數(shù)y的條件概率分布為：

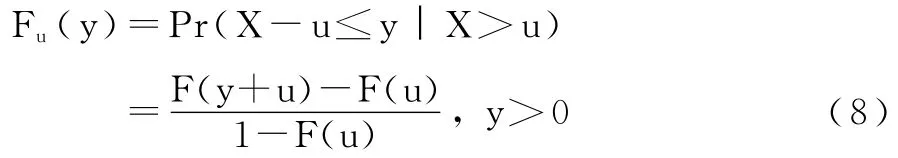
稱Fu（y）為超閾值分布。Balkema，Haan和Pickands［17，18］已證明，對(duì)充分大的閾值 u，超閾值分布近似為廣義帕累托分布：

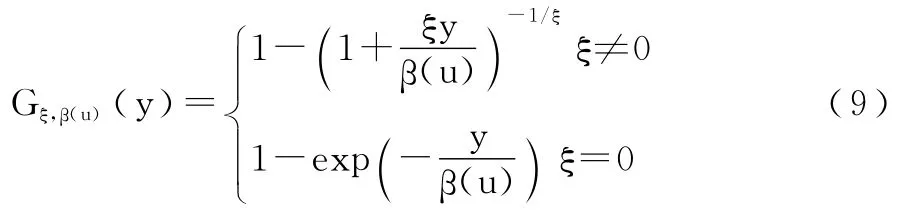
其中，β（u）為與u有關(guān)的正函數(shù)，表示尺度參數(shù)；ξ（∈R）為分布的形狀參數(shù)；尺度參數(shù)β（u）和形狀參數(shù)ξ決定著廣義帕累托分布的具體形狀。當(dāng)ξ≥0時(shí)，y≥0；當(dāng)ξ＜0時(shí)，0≤y≤-β（u）／ξ。當(dāng)ξ＞0時(shí)，F(xiàn)來自Fréchet分布簇，Gξ，β（u）為重新參數(shù)化的普通Pareto分布，它具有厚尾特征；當(dāng)ξ＝0時(shí)，F(xiàn)來自Gumbell分布簇，Gξ，β（u）為指數(shù)分布，它與指數(shù)分布相對(duì)應(yīng)，具有正常的尾部；當(dāng)ξ＜0時(shí)，F(xiàn)來自Weibull分布簇，Gξ，β（u）為paretoⅡ型分布，它具有薄尾特征。而ξ＞-0.5時(shí)，μ、β、ξ的最大似然估計(jì)符合一致的和漸近的正則分布，漸近的方差可以通過觀測(cè)信息矩陣的反函數(shù)求得；當(dāng)ξ＜-1時(shí)，最大似然估計(jì)一般不可能得到。在實(shí)際的極值建模中，當(dāng)ξ＞-0.5時(shí)，將很難遇到。當(dāng)ξ＞0時(shí)，廣義帕累托分布是厚尾的，這與本文的風(fēng)險(xiǎn)測(cè)度是最為相關(guān)的。

3.VaR與ES模型的估計(jì)

（1）閾值的選擇

在正確估計(jì)參數(shù)β和ξ之前，需要選擇合適的閾值。若閾值過高，將導(dǎo)致較少的超越量，估計(jì)方差較大；若閾值太小，將無法滿足超越量近似服從廣義帕累托分布的條件，會(huì)使得估計(jì)量成為有偏估計(jì)。因此，我們須權(quán)衡有偏和方差之間的關(guān)系，選擇適當(dāng)?shù)拈撝怠Ｏ旅娼榻B幾種較常用的確定閾值的方法。

①基于GPD的均值超額函數(shù)。均值超越函數(shù)e（u）可表示為：

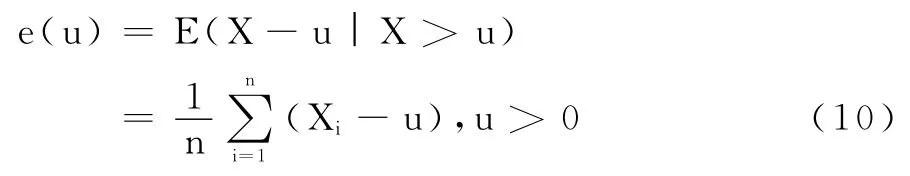
其中，Xi（i＝1，…，n）表示超過閾值的樣本觀測(cè)值，n為超越量個(gè)數(shù)。對(duì)某個(gè)閾值u0，如果超越量分布近似服從參數(shù)為β（u0）、ξ的廣義帕累托分布，則對(duì)大于u0的u、e（u）應(yīng)該為線性近似的。由此，定義點(diǎn)集｛（u，e（u））∶u＜max（Xi）｝，由這些點(diǎn)集構(gòu)成的圖形稱為平均剩余壽命圖（Mean Residual Life Plot）。選擇適當(dāng)?shù)膗0（＞0）作為閾值，可使得u≥u0的e（u）近似為線性。

② 觀察參數(shù)的穩(wěn)定性。在閾值取值范圍內(nèi)，利用超越量估計(jì)出GPD的參數(shù)β和ξ，若初始閾值u0對(duì)應(yīng)的超出量近似為廣義帕累托分布，則對(duì)大于u0的閾值形狀參數(shù)ξ的估計(jì)值應(yīng)該保持不變，且尺度參數(shù)有如下關(guān)系：

令β′＝β（u）-ξu，若β′與u無關(guān)，則稱式（11）為修正的尺度參數(shù)（Modified Scale）。由此，作β′和ξ關(guān)于u的圖形及與之相對(duì)應(yīng)的置信區(qū)間，并可選擇使這兩個(gè)估計(jì)量能保持為常數(shù)的最小值的u作為閾值。

③ Hill圖示法。令X（1）＞X（2）＞…＞X（n）表示獨(dú)立同分布的有序數(shù)列，尾部指數(shù)Hill的統(tǒng)計(jì)量可定義為：

在實(shí)際應(yīng)用中，我們常綜合運(yùn)用兩種或兩種以上的方法，以更準(zhǔn)確地確定閾值［23，24］。

（2）模型的估計(jì)

對(duì)參數(shù)β（u）和ξ的估計(jì)，我們將利用極大似然法得到。假設(shè)X1，X2，…，Xn為來自同一未知分布F的樣本觀測(cè)值，對(duì)于一給定的閾值u，稱滿足條件Xi-u＞0的樣本Xi為極值，分別用X（1），X（2），…，X（k）表示，并定義超閾值量yi＝X（i）-u（i＝1，2，…，k）。當(dāng)閾值u足夠大時(shí)，我們可以認(rèn)為超閾值量y1，y2，…yk為來自參數(shù)β（u）和ξ未知的廣義帕累托分布的隨機(jī)變量。為此，可建立樣本對(duì)數(shù)似然函數(shù)：

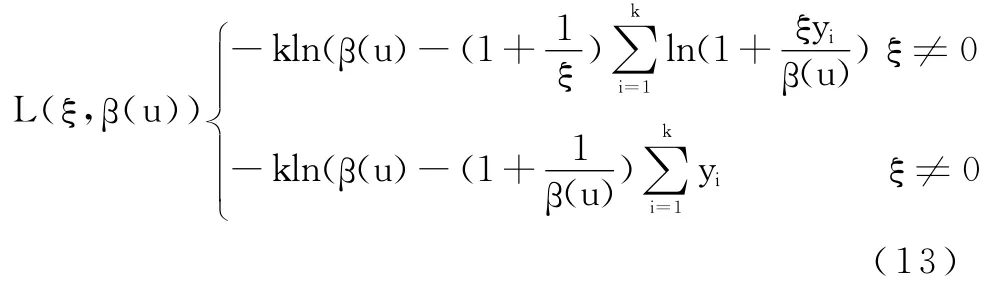
為估計(jì)損失分布的尾部，在等式（8）中令X＝y(tǒng)＋u；對(duì)足夠大的閾值 u，我們有 Fu（y）≈Gξ，β（u）（y），并將其帶入（8）式得：

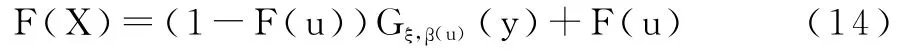
對(duì)（14）式的函數(shù)F（u），我們可用經(jīng)驗(yàn)累計(jì)分布函數(shù)值F（u）＝（n-k）／n來替代（k代表超越閾值u的樣本觀測(cè)值個(gè)數(shù)），這樣，我們可以得到：

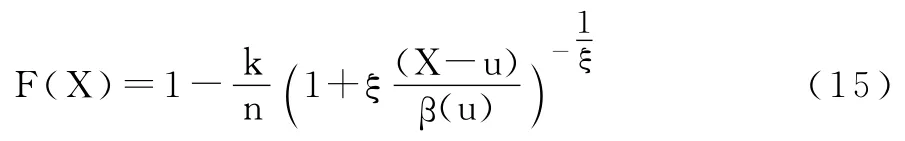
4.后驗(yàn)測(cè)試

為檢驗(yàn)非交易風(fēng)險(xiǎn)計(jì)量模型的有效性，本文將分別對(duì)它們進(jìn)行后驗(yàn)測(cè)試。所謂后驗(yàn)測(cè)試（Backtesting）就是用統(tǒng)計(jì)方法估算的數(shù)值結(jié)果對(duì)實(shí)際損失的覆蓋程度。事實(shí)上，通過比較過去一段時(shí)間內(nèi)期貨收益的實(shí)際損失金額超過用模型估算的VaR值（或ES值）的次數(shù)（穿越次數(shù)）是否趨近于違約概率，來驗(yàn)證基于EVT的VaR（或ES）是否符合模型設(shè)定的違約概率，以此來檢測(cè)所建模型的準(zhǔn)確性。由此，各期貨樣本VaR（或ES）的溢出率為：

VaR（或ES）的E值將與設(shè)定的顯著水平1-q相比較，進(jìn)而來判斷模型的準(zhǔn)確性。當(dāng)置信水平為q時(shí)，若E值大于1-q，說明非交易的風(fēng)險(xiǎn)水平較低；反之，若E值小于1-q，說明非交易的風(fēng)險(xiǎn)水平較高。總之，E值越是接近于1-q，說明模型建立得越準(zhǔn)確。

四、實(shí)證研究

（一）數(shù)據(jù)選擇

目前，我國(guó)期貨市場(chǎng)上的主力期貨品種包括上海期貨交易所（SHFE）的鋁、銅和橡膠、大連商品交易所（DCE）的大豆、鄭州商品交易所（ZCE）的小麥（硬麥）。這些期貨合約及其交易比較成熟，可以作為我國(guó)期貨市場(chǎng)的代表。由于我國(guó)期貨合約具有非連續(xù)的特點(diǎn)，因此，鋁和銅選擇3月期、橡膠選擇2月期、大豆選擇4月期、小麥選擇2月期每個(gè)交易日開盤和收盤價(jià)格的連續(xù)數(shù)據(jù)［19］，其時(shí)間跨度為1995年6月1日至2009年6月30日，所產(chǎn)生的鋁、銅、橡膠、大豆和小麥期貨樣本數(shù)據(jù)分別為3368、3432、2712、3263和2695個(gè)。期貨價(jià)格數(shù)據(jù)來源于相應(yīng)的期貨交易所和國(guó)聯(lián)倚天數(shù)據(jù)庫(kù)。

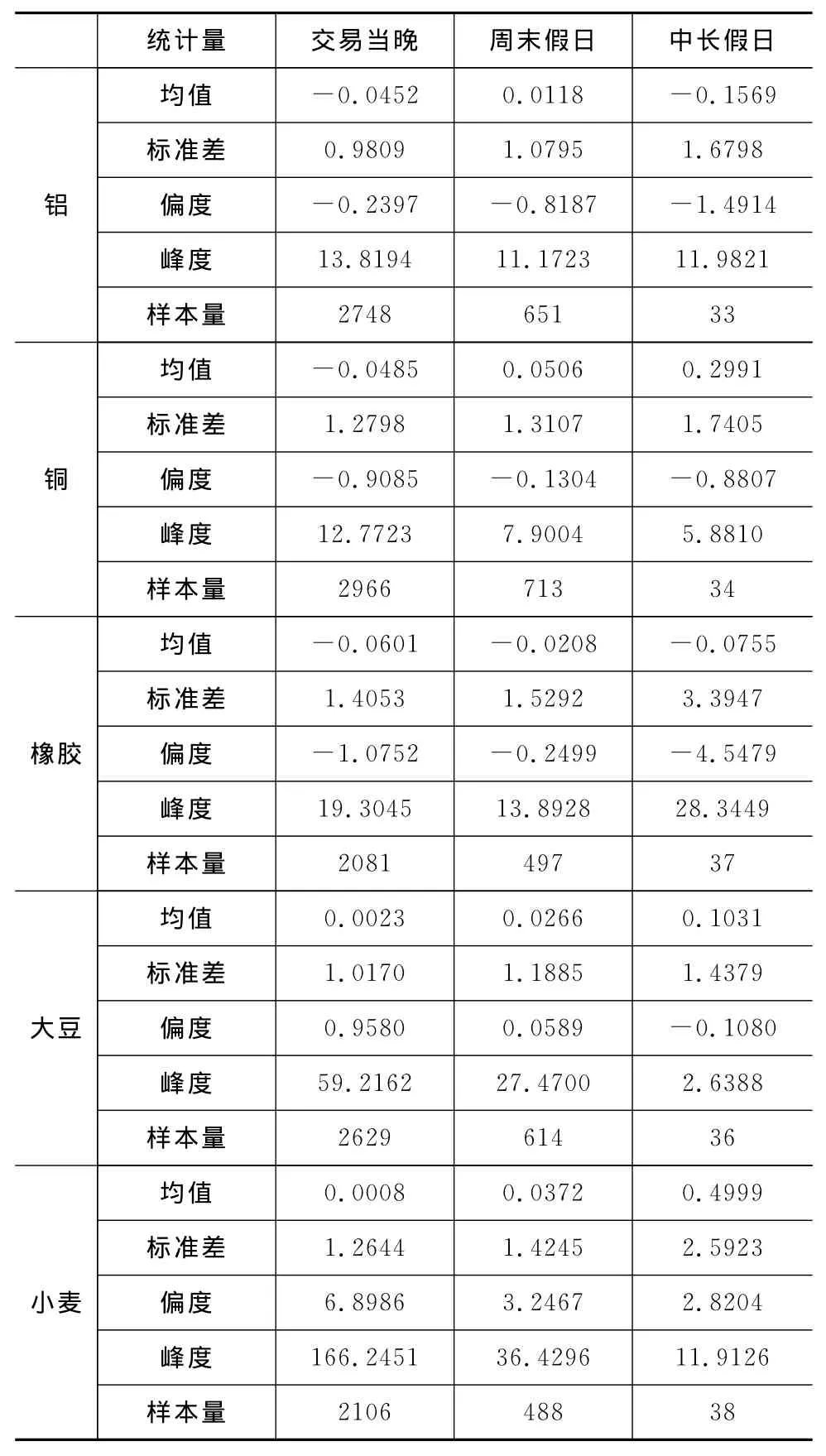
表1 期貨非交易收益的基本統(tǒng)計(jì)量① 類似于Tsiakas（2008）的貢獻(xiàn)度檢測(cè)和Granger因果檢驗(yàn)，在5%的置信水平下，交易當(dāng)晚、周末假日和中長(zhǎng)假日的收益對(duì)傳統(tǒng)收益和日間交易均具有顯著影響；為保持論文的完整性和節(jié)省篇幅，對(duì)它們的論證則從略。

（二）非交易收益的基本統(tǒng)計(jì)特征

表1給出了非交易收益的基本統(tǒng)計(jì)量。可以看出，各期貨合約不同時(shí)段的非交易收益均表現(xiàn)出不同的正、負(fù)收益特性，非交易收益的偏度也表現(xiàn)出不同的左偏和右偏特征；并且，各期貨合約不同時(shí)段的非交易收益的峰度均大于正態(tài)分布的峰度3，由此說明各非交易收益均具有尖峰厚尾特征。從標(biāo)準(zhǔn)差來看，各期貨合約交易當(dāng)晚、周末假日和中長(zhǎng)假日的標(biāo)準(zhǔn)差呈遞增態(tài)勢(shì)，這說明隨著非交易時(shí)間的累積，非交易收益的風(fēng)險(xiǎn)會(huì)逐漸增大；且總體而言，銅、橡膠和小麥?zhǔn)袌?chǎng)非交易收益的標(biāo)準(zhǔn)差較大，鋁和大豆市場(chǎng)非交易收益的標(biāo)準(zhǔn)差相對(duì)較小。

（三）非交易風(fēng)險(xiǎn)的測(cè)度

1.閾值選擇及分布參數(shù)估計(jì)

采用POT方法估計(jì)VaR與ES的值，先要確定閾值。從精度出發(fā)，各序列閾值的選取我們將結(jié)合平均剩余壽命圖和觀察不同閾值下參數(shù)的穩(wěn)定性來共同確定。下圖1給出了鋁期貨交易當(dāng)晚、周末假日和中長(zhǎng)假日收益序列的剩余壽命圖及不同閾值下的參數(shù)變化圖①銅、橡膠、大豆和小麥的圖與此類似。。根據(jù)圖1，我們可分別確定對(duì)應(yīng)序列的閾值，然后再根據(jù)極大似然法估計(jì)對(duì)應(yīng)序列的尺度參數(shù)和形狀參數(shù)，表2給出了各期貨不同非交易收益的閾值及尾部參數(shù)估計(jì)結(jié)果。

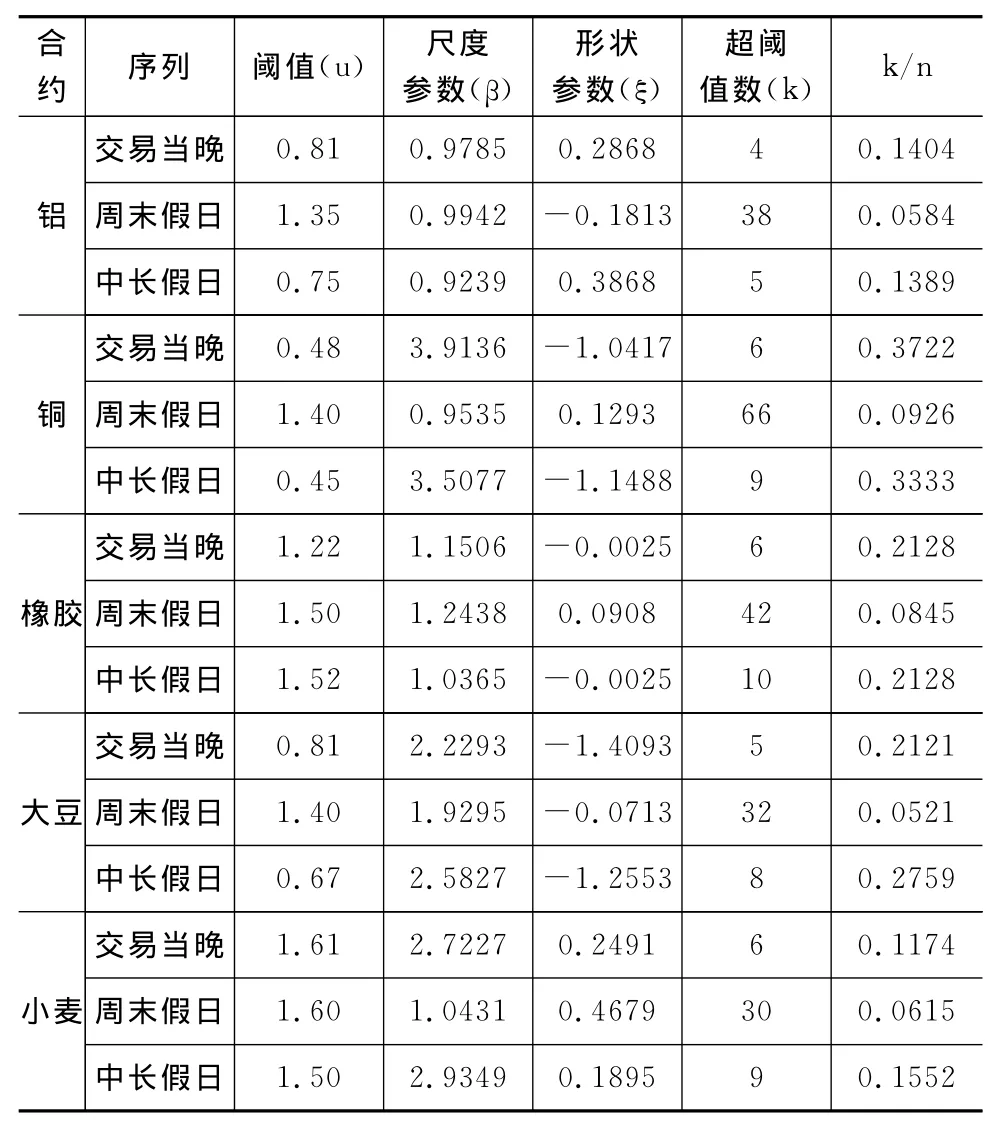
表2 各序列閾值及尾部參數(shù)估計(jì)值

在確定損失的尾部極值分布時(shí)，我們常采用P-P圖和Q-Q圖來檢驗(yàn)?zāi)Ｐ偷臄M合程度。為此，利用上文估計(jì)結(jié)果，我們可進(jìn)一步得到各期貨市場(chǎng)不同非交易收益序列GPD擬合的診斷圖（如圖2所示）。可以發(fā)現(xiàn)，所有的點(diǎn)都幾乎在一條直線上，密度曲線的估計(jì)與直方圖也相吻合，由此說明根據(jù)前文所提方法的參數(shù)估計(jì)是恰當(dāng)?shù)摹?/p>

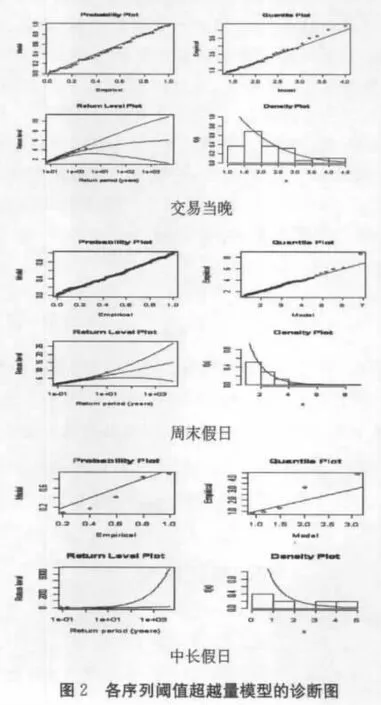
2.VaR與ES的估計(jì)結(jié)果

在滿足上述假設(shè)的條件下，我們來估計(jì)95%和99%置信水平下的VaR與ES估計(jì)值。參數(shù)u、β、ξ估計(jì)出以后，利用（4）式和（7）式，即可計(jì)算出各期貨市場(chǎng)不同非交易收益的風(fēng)險(xiǎn)價(jià)值（VaR）及其預(yù)期損失（ES）（以日作為持有期），并對(duì)其相應(yīng)估計(jì)結(jié)果進(jìn)行了后驗(yàn)測(cè)試（如表3所示）。

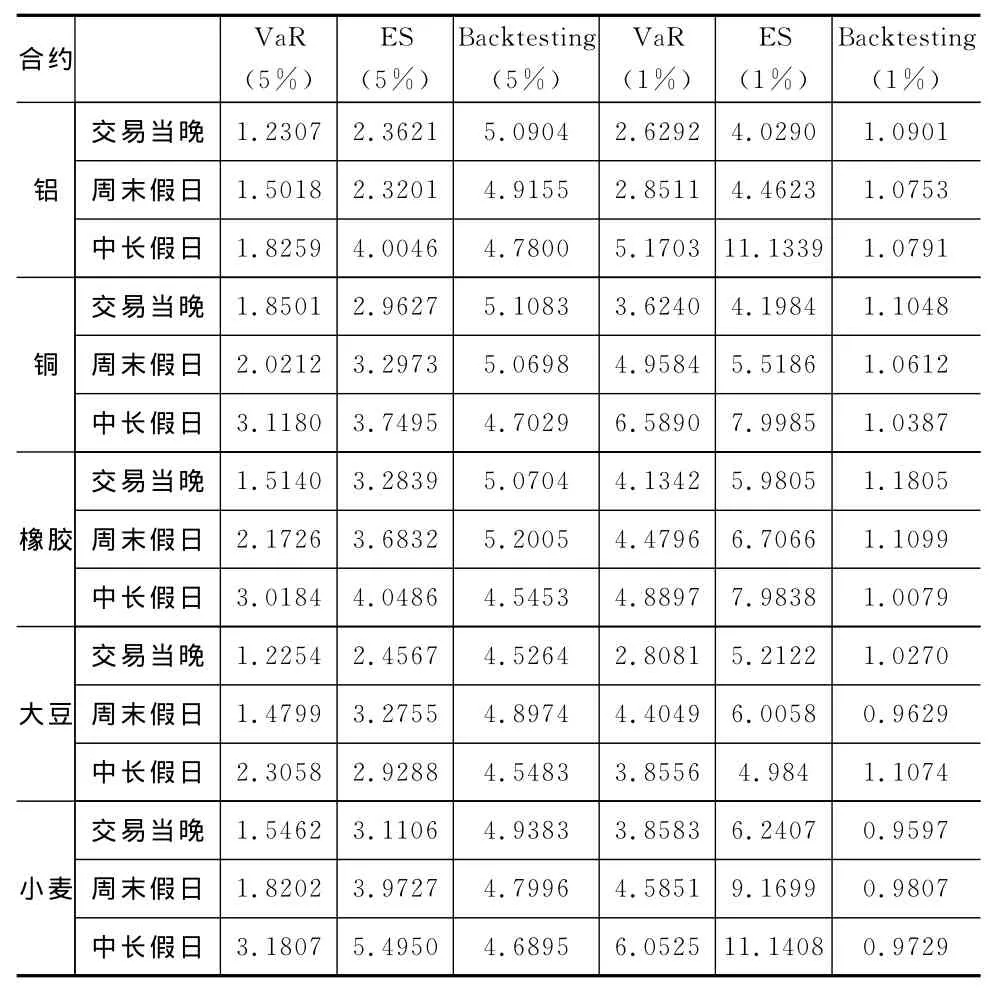
表3 各序列的風(fēng)險(xiǎn)價(jià)值及其預(yù)期損失估計(jì)值

表3給出了鋁、銅、橡膠、大豆和小麥序列VaR和ES的估計(jì)值及其后驗(yàn)測(cè)試結(jié)果。根據(jù)后驗(yàn)測(cè)試結(jié)果可知，基于極值理論的VaR和ES模型可以比較好地描述期貨市場(chǎng)非交易時(shí)段的風(fēng)險(xiǎn)價(jià)值及其預(yù)期損失。從縱向來看，對(duì)于每一期貨交易品種，交易當(dāng)晚、周末假日和中長(zhǎng)假日的風(fēng)險(xiǎn)價(jià)值及其預(yù)期損失均呈遞增態(tài)勢(shì)。由此說明，我國(guó)期貨市場(chǎng)非交易時(shí)間與非交易風(fēng)險(xiǎn)之間呈正向關(guān)系。也就是說，隨著時(shí)間的累積，非交易時(shí)間的信息含量會(huì)逐漸增多，非交易風(fēng)險(xiǎn)也會(huì)隨之增大，這也與前文非交易收益的標(biāo)準(zhǔn)方差具有遞增特征相吻合。之所以出現(xiàn)這一狀況，主要是于非交易時(shí)段所包含的大量私人信息和公共信息以及不同地區(qū)期貨交易的非同步性有關(guān)［20，21］。這樣，隨著時(shí)間的延續(xù)，新信息積累到一定程度就會(huì)影響投資者的買賣行為，從而造成期貨價(jià)格的波動(dòng)［20］。一般而言，兩個(gè)相鄰交易日之間的非交易時(shí)間越長(zhǎng)，累積的信息會(huì)越多，重新開盤時(shí)期貨價(jià)格的波動(dòng)也就越大，這就不可避免地導(dǎo)致期貨市場(chǎng)非交易風(fēng)險(xiǎn)的增大。

從橫向來看，在95%的置信水平下，銅和橡膠市場(chǎng)的非交易風(fēng)險(xiǎn)較大，小麥?zhǔn)袌?chǎng)次之，大豆和鋁市場(chǎng)相對(duì)較小；在99%的置信水平下，橡膠和小麥?zhǔn)袌?chǎng)的非交易風(fēng)險(xiǎn)較大，銅和大豆次之，鋁市場(chǎng)最小。總體而言，銅、橡膠和小麥?zhǔn)袌?chǎng)的非交易風(fēng)險(xiǎn)較大，而鋁和大豆市場(chǎng)的非交易風(fēng)險(xiǎn)相對(duì)較小，這與前文期貨市場(chǎng)非交易收益的標(biāo)準(zhǔn)方差大小描述是相一致的。在非交易時(shí)段，不同期貨市場(chǎng)非交易風(fēng)險(xiǎn)存在上述差異的原因有哪些呢？其緣由主要可歸結(jié)為各期貨市場(chǎng)非交易新信息在市場(chǎng)內(nèi)部和市場(chǎng)外部的獲取方面［22，23］。與前者不同，小麥?zhǔn)袌?chǎng)相對(duì)狹小，市場(chǎng)也不太活躍；特別是作為標(biāo)的物的小麥現(xiàn)貨，長(zhǎng)期受國(guó)家農(nóng)業(yè)政策的制約和自然災(zāi)害的影響，等等。以上這些因素，會(huì)使得銅、橡膠和小麥期貨在非交易時(shí)段的新信息累積相對(duì)較大，這自然加大了市場(chǎng)的非交易風(fēng)險(xiǎn)。然而，與銅、橡膠和小麥相比，鋁和大豆期貨及其現(xiàn)貨的供需基本平衡，市場(chǎng)也較為成熟［23，24］，且相對(duì)而言，既存在較少的來自國(guó)外重大消息的影響，也較少受到來自國(guó)內(nèi)經(jīng)濟(jì)政策等消息的沖擊。總的來說，鋁和大豆期貨市場(chǎng)來自國(guó)內(nèi)外新信息的累積相對(duì)較小，這也自然不會(huì)導(dǎo)致市場(chǎng)的大幅波動(dòng)，因而非交易風(fēng)險(xiǎn)也比較小①事實(shí)上，不同期貨市場(chǎng)的非交易風(fēng)險(xiǎn)存在個(gè)體差異的原因是非常多的，限于篇幅，這里只列出了幾個(gè)較重要原因。。此外，置信水平的選擇對(duì)風(fēng)險(xiǎn)價(jià)值及其預(yù)期損失的影響也是非常明顯的，當(dāng)置信水平從95%增加到99%時(shí)，風(fēng)險(xiǎn)價(jià)值增加了一倍以上，其預(yù)期損失增加了近兩倍，這說明風(fēng)險(xiǎn)價(jià)值和預(yù)期損失對(duì)置信水平的選擇非常敏感，預(yù)期損失比風(fēng)險(xiǎn)價(jià)值變化得更快，這也與風(fēng)險(xiǎn)價(jià)值和預(yù)期損失的理論定義相符。

五、結(jié)論與啟示

本文在分析交易當(dāng)晚、周末假日與中長(zhǎng)假日收益基本統(tǒng)計(jì)量的基礎(chǔ)上，系統(tǒng)測(cè)度了各期貨市場(chǎng)不同非交易收益的風(fēng)險(xiǎn)價(jià)值及其預(yù)期損失。實(shí)證結(jié)果顯示：（1）基于極值理論的VaR和ES模型可以較好地描述期貨市場(chǎng)非交易時(shí)段的風(fēng)險(xiǎn)價(jià)值及其預(yù)期損失；（2）從縱向來看，交易當(dāng)晚、周末假日和中長(zhǎng)假日的風(fēng)險(xiǎn)價(jià)值及其預(yù)期損失均呈逐漸遞增態(tài)勢(shì)，這意味著我國(guó)期貨市場(chǎng)非交易時(shí)間與非交易風(fēng)險(xiǎn)之間呈正向關(guān)系，即隨著時(shí)間的累積，非交易時(shí)段的信息含量會(huì)逐漸增多，非交易風(fēng)險(xiǎn)也會(huì)逐漸增大；由此表明，非交易時(shí)段所積累的金融信息具有顯著的預(yù)測(cè)能力。（3）從橫向來看，在95%的置信水平下，銅和橡膠市場(chǎng)的非交易風(fēng)險(xiǎn)較大，小麥?zhǔn)袌?chǎng)次之，大豆和鋁市場(chǎng)相對(duì)較小；而在99%的置信水平下，橡膠和小麥?zhǔn)袌?chǎng)的非交易風(fēng)險(xiǎn)較大，銅和大豆次之，鋁市場(chǎng)最小。

以上研究結(jié)論有利于充分認(rèn)識(shí)和把握我國(guó)各期貨市場(chǎng)及不同非交易時(shí)段的非交易風(fēng)險(xiǎn)，以及非交易時(shí)間與非交易風(fēng)險(xiǎn)之間的正向關(guān)系，對(duì)我國(guó)期貨市場(chǎng)投資者和風(fēng)險(xiǎn)管理當(dāng)局來說均具有一定的實(shí)踐指導(dǎo)意義。一方面，投資者可以利用非交易時(shí)間與非交易風(fēng)險(xiǎn)之間的正向關(guān)系來優(yōu)化投資者的投資決策，可以利用不同期貨非交易風(fēng)險(xiǎn)的差異性來規(guī)避非交易風(fēng)險(xiǎn)對(duì)期貨交易的影響，還可以為期貨市場(chǎng)的價(jià)格發(fā)現(xiàn)提供預(yù)測(cè)。另一方面，這一研究還可以為風(fēng)險(xiǎn)管理當(dāng)局進(jìn)行風(fēng)險(xiǎn)測(cè)度、風(fēng)險(xiǎn)管理制度的制定以及風(fēng)險(xiǎn)監(jiān)管策略的設(shè)計(jì)等提供必要的方法和信息支持，期貨市場(chǎng)管理者可根據(jù)非交易時(shí)段的長(zhǎng)短有針對(duì)性地制定市場(chǎng)風(fēng)險(xiǎn)防控措施，為防范和化解非交易風(fēng)險(xiǎn)服務(wù)，實(shí)現(xiàn)期貨市場(chǎng)非交易性風(fēng)險(xiǎn)的有效監(jiān)管。

［1］Taylor N.A Note on the Importance of Overnight Information in Risk Management Models［J］.Journal of Banking and Finance，2007，31：161–180.

［2］Tsiakas I.Overnight Information and Stochastic Volatility：A Study of European and US Stock Exchanges［J］.Journal of Banking ＆Finance，2008，32：251–268.

［3］Baumol W.An Expected Gain-confidence Limit Criterion for Portfolio Selection［J］.Management Science，2008，10：174-182.

［4］Artzner P F，Delbaen J，Eber，Heath D.Coherent Measures of Risk［J］.Mathematical Finance，1999，9：203-228.

［5］Engle R F，Manganelli S.CVaR：Conditional Value at Risk by Quantile Regression［C］.NBER Working Papers 1999，No.7341，National Bureau of Economic Research，Inc.

［6］Manganelli S，Engle R F.Value at Risk Models in Finance［C］.Working Paper Series，No.075，European Central Bank，2001.

［7］Acerbi C，Tashe D.On the Coherence Expected Shortfall［J］.Journal of Banking and Finance，2002，26：1487-1503.

［8］Frey R，McNeil A.VaR and Expected Shortfall in Portfolios of Dependent Credit Risks：Conceptual and Practical Insights［J］.Journal of Banking and Finance，2002，26：1317–1344.

［9］Rockafellar R，Uryasev T S.Optimization of Conditional Value-at-risk［J］.Journal of Risk，2000，3：21-41.

［10］Tsay.Analysis of Financial Time Series［M］.John Wiley ＆Sons，Inc.2002.

［11］Longin F M.Optimal Margin Levels in Futures Markets：Extreme Price Movements［J］.Journal of Futures Markets，1999，19：127-152.

［12］遲國(guó)泰，王玉剛，汪紅梅.基于多元GARCH-VaR的期貨組合保證金模型及其應(yīng)用研究［J］.預(yù)測(cè)，2008，27（5）：49-57.

［13］韓德宗.基于VaR的我國(guó)商品期貨市場(chǎng)風(fēng)險(xiǎn)的預(yù)警研究［J］.管理工程學(xué)報(bào)，2008，22（1）：117-121.

［14］劉慶富，仲偉俊，華仁海，等.EGARCH-GED模型在計(jì)量我國(guó)期貨市場(chǎng)風(fēng)險(xiǎn)價(jià)值中的應(yīng)用［J］.管理工程學(xué)報(bào)，2007（1）：117-121.

［15］Rockafellar R，Uryasev T S.Conditional Value-at-risk for General Loss Distribution［J］.Journal of Banking ＆Finance，2002，26：1443-1471.

［16］Matthys G，Beirlant J.Estimating the Extreme Value Index and High Quantiles with Exponential Regression Models［J］.Statistica Sinica，2003，13：853-880.

［17］Balkema A，de Haan L.Residual Life Time at Great Age［J］.Annals of Probability，1974（2）：792–804.

［18］Pickands J.Statistical Inference using Extreme Order Statistics［J］.The Annals of Statistics，1975（3）：119–131.

［19］丁秀玲，華仁海.大連商品交易所大豆與豆粕期貨價(jià)格之間的套利研究［J］.統(tǒng)計(jì)研究，2007，24（2）：55-59.

［20］French K，Roll R.Stock Return Variances：The Arrival of Information and the Reaction of Traders［J］.Journal of Financial Economics，1986，17：5–26.

［21］del Corral W，Colwell D，Michayluk D.News Releases when Markets are Closed［C］.Unpublished working paper，University of Technology Sydney，2003.

［22］Frank J F，Christopher K M，James E B.Holiday Trading in Futures Markets［J］.Journal of Finance，1994，49（1）：307-324.

［23］劉慶富.中國(guó)期貨市場(chǎng)的隔夜信息能否影響日間交易價(jià)格——基于貝葉斯 MCMC推斷的隨機(jī)波動(dòng)模型［C］.第八屆中國(guó)金融學(xué)年會(huì)，山東大學(xué)，2011.

［24］Liu Q，Huang B，An Y.Risk contributions of trading and non-trading hours：Evidence from commodity futures markets［C］.Working paper，F(xiàn)udan University and the University of Windsor.2010，12.