把握本質屬性 促進有效教學

袁政

【中圖分類號】G623.5 【文獻標識碼】A 【文章編號】2095-3089（2013）08-0156-01

學生掌握基礎知識的過程，實際上就是掌握概念并運用概念進行判斷、推理的過程。我認為有效的幾何概念教學，就是幫助學生把握住其本質屬性，剔除其非本質屬性，優化學生學習過程。本人從“三角形的認識”和“圓的認識”這兩方面的教學說說我們的想法，與大家商榷。

一、提供豐富的感性材料，把握概念的本質特征

眾所周知，影響幾何概念學習的因素之一就是感性材料和感性經驗的數量與質量。感性材料和感性經驗太少或不典型，學生的感知就會不充分，表象也就不可能豐富，也就難以抽象出概念的本質屬性。數學來自現實生活，生活中處處有數學，結合生活實際引入概念符合小學生的心理特點和認知規律。

如，在教學三角形的特點時，我讓學生思考：在實際生活中哪些地方用到了“三角形”？（課件顯示圖）自行車的三角架、支撐房頂的梁架、電線桿上的三角架等，為什么都做成三角形而不做成四邊形呢？通過生活中的實例，來提示三角形具有穩定性的特點。

又如，在教學《圓的認識》時，我先是讓學生看到（課件顯示圖）車輪、硬幣、表盤、井蓋、餐桌、瓶蓋等。產生了問題：“這些物體為什么做成圓的？”引起學生興趣空前高漲。捕捉“生活現象”，創設問題情境來學習，既把握了概念的本質屬性，又讓學生感覺數學就在自己身邊，它不再是枯燥的，而是無比有趣的。我們一定要注意，提供的材料與所探索知識間的內在聯系，把握概念的本質屬性，要有實用性，少走彎路。

二、充分運用變式規律，抓住概念的本質屬性

所謂變式，是指將概念的正例（一切符合概念范圍的具體實例）加以變化，提供的事例或材料不斷地變換呈現形式，改變非本質屬性，使本質屬性“恒在”，借此可以幫助學生準確形成概念，防止學生在概念的理解上的片面性。特別是出示幾何圖形時位置要變化，不要讓其“經典式出場”。

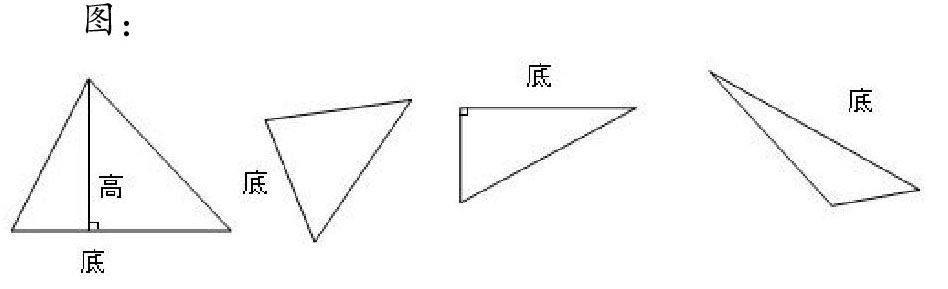
如教學三角形的高，我首先呈現三角形高的標準圖形（課件顯示圖），然后呈現三角形高的非標準圖形，讓學生做指定底的高。通過呈現三角形高的“標準圖形與非標準圖形”，擴大概念的外延，防止學生因教學中所使用的只是“標準圖形”，而產生“三角形的高只有一條”，“三角形的高必須處于與水平方向垂直的位置”，“三角形的高必在三角形內”等錯誤觀念，將相關實例的某些特殊性質誤認為是概念的本質屬性。

圖：

利用變式，讓學生從不同角度、不同層次進行探討，教師有目的地引導學生從“變”的現象發現“不變”的本質，由“不變”的本質探索“變”的規律，真正有效地掌握概念。

三、充分運用正反例證，突出概念的本質屬性

在學習過程中，正確與錯誤的理解是對立存在的，糾正了理解上的片面性認識，認識就會向前邁進。學習數學概念也是如此，合理使用反例進行教學將有利于克服學生在感知上的缺陷。

我在教學圓的認識時反例用的比較多。

如示范用圓規畫圓時，第一次我開始故意移動有針尖的一腳，同學們著急，說出畫不好的原因，我順勢強調“定點”——“圓心”；第二次，我故意慢慢地把圓規兩腳越分越開，結果沒有畫成一個圓。同學們在笑，笑的過程也有思考。我說：“老師真笨，怎么就畫不好呢？”細心的同學說出了原因。我順勢強調畫圓時圓規兩腳間的距離是不變的，這個定長就是半徑。抓住圓的本質屬性。

如教學“圓的認識”，認識了圓的特征后，有這么一段：

我：車輪做成哪種形狀好呢？

生齊答：圓形。

我：是嗎？請看屏幕！師演示課件，屏幕上出現一輛車，車輪是圓形的，只是車軸不在圓心，車顛簸地向前行。

學生哈哈大笑，教師按停課件：問題出在哪兒呢？

學生靜了一會兒，有人舉手提出車軸應該安在圓心。

我：為什么？可以用所學的知識加以說明嗎？

生：因為圓心到圓上任意一點的距離相等。車軸安在圓心車才平穩。

教學中，我根據學生的回答故意舉出反例，把車軸不安裝在圓心，引發學生的思考，突出概念的本質特征。

當然，并非反例運用越多越好。一方面要善于抓住學生課堂上、作業里“展現”出來的現實反例，不失時機地進行深入細致的分析；另一方面要適時根據學生在課堂上的表現機智地“引”出反例，供學生進行辨析，以防類似錯誤的再發生。尤其是要讓學生通過對比正例與反例的差異，對自己的錯誤進行反思，強化學生對本質屬性的理解。

四、剖析關鍵詞的含義，明確概念的本質屬性

定義是揭示數學概念本質屬性確切而精煉的說明。要使學生對概念有完整、深刻的理解，必須深刻剖析定義，揭示定義中關鍵性詞語、術語或符號的意義。

對定義的分析是幫助學生認識概念的又一次提高，如教學圓的半徑定義時，理解“圓上任意一點”的含義，應讓學生在畫圓過程中體會到圓上有無數多個點；在確定兩個端點位置時，教師要使學生體會到：半徑的一個端點在圓心，另一個端點在圓上，這個端點具有任意性，最后將其概括為“圓上的任意一點”，從而使學生從半徑的外延方面進一步理解半徑的概念。學生既知道從圓心到圓上任意一點的線段都叫作半徑，又知道一個圓中有無數條半徑。

又如，教學三角形的概念時強調“圍成”這個關鍵詞。在教學三角形的高的定義時，要強調“頂點”是相對于“對邊”而言的等。

在教學概念時，教師要指導學生抓住概念的要點和關鍵性的字詞，并用紅筆加上著重符號，以強化注意。我也贊同有的老師讓學生讀概念時，關鍵詞語重音讀的做法。這樣，學生既能深刻理解概念，又可以提高記憶效率，學生既知其然又知其所以然，收到事半功倍的效果。

課題研究反思：

有效的幾何概念教學，必須遵循概念的形成及學生認知發展的規律，經歷由淺入深、由具體到抽象再到具體應用的過程。只有抓住概念的本質屬性進行教學，才能有效促進學生思維的發展。

時下，眾多的幾何概念教學的觀摩課、比賽課，設計新穎、精彩紛呈，也讓人眼花繚亂。教師們紛紛效仿，所謂“雖不能至，心向往之”。山寨版層出不窮并非壞事，但只有適合自己風格的，才能發揮更好的效用。“一雙精美的鞋，并不一定適合自己的腳”，作為教師，我們不必盲從。如何把一些抽象的數學概念變為小學生看得見、摸得著、理解得了的數學事實？這是我們在教學實踐中必須要深入考慮的問題。