淺談平面桿件體系幾何構造分析的方法

黃志剛

湖南文理學院土木建筑工程學院, 湖南 常德 415000

引言

結構力學中的平面桿件體系的幾何構造分析，其目的在于（1）判別某一體系是否為結合不變，從而決定它能否作為結構;（2）區別靜定結構，超靜定結構，從而選擇相應的計算方法;（3）搞清楚結構各部分之間的相互關系，以決定合理的計算順序。從其目的不難看出它是結構力學的重要內容之一。在平面桿件體系的幾何構造分析中，最基本的規律是鉸結三角形規律。規律本身是簡單淺顯的，但規律的運用則變化無窮[1]。因此，學習時遇到的困難不在于學懂規律，而在于如何運用規律。鑒于現行教科書對規律運用的平泛講解[2]，筆者結合自身學習與教學經驗，總結出平面桿件體系幾何構造分析的方法并舉例加以說明，以期對學生的學習有一定的幫助。

1 幾何構造分析的方法

1.1 考察體系的計算自由度

根據計算自由度W的數值與體系的幾何構造特性之間的關系知，如果，對象體系的自由度總數大于約束總數，體系為幾何可變，則可不必再進行幾何構造分析。否則，則應進行幾何構造分析。基于此，對于某些無論采取何種方法都無法入手的問題，該法是一種捷徑。

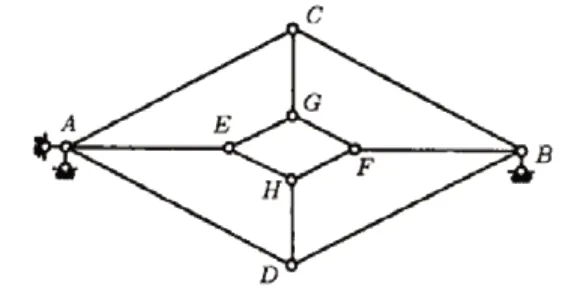
圖1

1.2 拆去二元體，簡化體系，然后再分析

所謂“二元體”是指由兩根不共線的鏈桿聯結一個新點的裝置[3]。利用此方法時，要注意判別二元體，二元體的形式多種多樣，常見的形式如圖2所示。

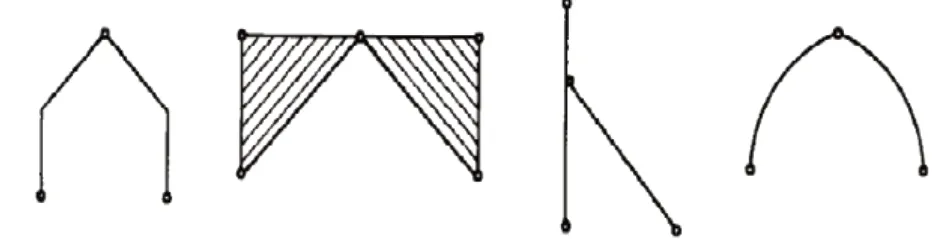
圖2

圖3

對于圖3所示的平面桿件體系，看上去較為復雜，但在依次去掉二元體J，I，H，G，E，C，D后就只剩下地基，由于地基是幾何不變的，根據二元體規則可判定該體系為無多余約束的幾何不變體系。

1.3 當體系與基礎用滿足要求的三個約束相聯時，則可以拋開基礎，只分析體系本身即可

對于圖4所示平面桿件體系，上部桿系和基礎是按兩剛片法則組成，則體系的幾何構造屬性取決于上部桿系，因而可把基礎拋開，只分析上部。上部桿系由左邊剛片A-C-D-E和右邊剛片B-C-E-G通過一鉸C和鏈桿F-G相聯，根據兩剛片規則可以判斷該體系為無多余約束的幾何不變體系。

1.4 當體系桿件數較多時，將剛片選得“分散”些，剛片與剛片間用鏈桿形成的瞬鉸相聯，而不用單鉸相聯

對于圖5所示體系，如將基礎、ADE、EFC作為剛片，將找不出兩兩相連的三鉸。如果將剛片選得“分散些”，例如選擇鉸結三角形EFC、鏈桿BD、基礎（包括固定鉸支座A）分別作為剛片I，Ⅱ，Ⅲ，并用鏈桿BF、DE形成的瞬鉸O12，鏈桿AD、支座B形成的瞬鉸O23,鏈桿AE、支座C形成的瞬鉸O13相聯，則發現三剛片用三個不共線的鉸兩兩相聯，根據三剛片規則可判定該體系為無多余約束的幾何不變體系。

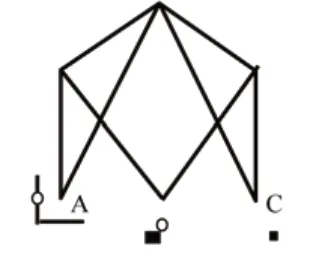
圖5

1.5 由一基本剛片（單根鏈桿或鉸結三角形）開始，逐步增加二元體，擴大剛片的范圍，將體系歸結為兩剛片或三剛片相聯，然后用規則判定

圖6所示平面桿件體系，上部桿系和基礎符合兩剛片規則，在分析時首先拋開基礎，只分析上部。然后在體系內確定三個剛片：在鉸結三角形1-2-11的基礎上依次增加二元體2-12-11,2-3-12，11-10-12形成擴大的剛片1-2-3-12-10-11；同理，在鉸結三角形7-8-9的基礎上依次增加二元體9-13-7,7-6-13,9-10-13形成擴大的剛片6-7-8-9-10-13；在鉸結三角形3-4-5的基礎上增加二元體4-6-5形成擴大的剛片3-4-5-6。三個擴大的剛片用三個不共線的三鉸3,6,10相聯，根據三剛片規則可以判定該體系是無多余約束的幾何不變體系。

圖6

1.6 由基礎開始逐件組裝

如果體系與基礎之間的約束多于三個，則可以從基礎出發進行裝配。圖7所示體系，桿1與基礎通過支座A、B連接成一個剛片，把桿2看作一個剛片，兩剛片由交于C點的鏈桿3,4,5相聯，根據兩剛片規則可判定該體系為幾何可變體系。

圖7

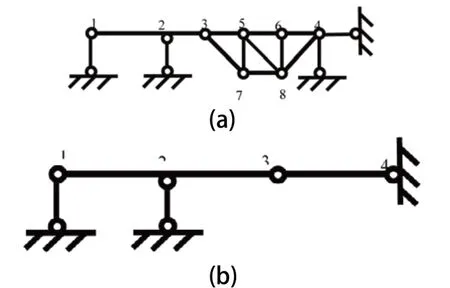
圖8

1.7 利用剛片的等效代換

在不改變剛片與周圍物體聯結方式的前提下，可以改變它的大小，形狀及內部組成。即可以用一個等效剛片（與外部聯結等效）代替原剛片。

對于圖8(a)所示體系，在鉸結三角形3-5-7的基礎上依次增加二元體5-8-7,5-6-8,6-4-8可構成一個大剛片3-5-6-4-8-7，在不改變該大剛片與周圍物體聯結的前提下，將其用一根直桿3-4代換，另將題目中相交的兩根鏈桿用一個鉸代換，則體系等效為圖8(b)所示體系。此時，剛片1-2-3通過支座1,2, 鏈桿3-4與基礎相聯，由兩剛片規則可以判定該體系為無多余約束的幾何不變體系。

2 結束語

以上闡述的平面桿件體系幾何構造分析的方法，是根據筆者的教學經驗以及總結學生在學習該項內容過程中遇到的問題經分析提煉而成的。按照上述方法，加上一定量的練習，相信掌握這部分內容就比較容易了。

[1]龍馭球,包世華,袁駟.結構力學I——基本教程[M]. 第3版.北京:高等教育出版社,2012,8:15-24.

[2]張韜. 淺談幾何構造分析中的轉換[J]. 大眾科技，2012,8:177-178.

[3]李家寶. 結構力學[M].第3 版. 北京:高等教育出版社，1999,6:11-20.