尋找那個(gè)最近的生長(zhǎng)點(diǎn)——一節(jié)參賽課的難點(diǎn)分析與突破

☉江蘇省連云港市新壩中學(xué) 趙文龍

☉江蘇省連云港市新壩中學(xué) 周 楊

2012年12月上旬，筆者參加了連云港市初中數(shù)學(xué)教師優(yōu)質(zhì)課比賽區(qū)級(jí)預(yù)賽.課題為蘇科版數(shù)學(xué)八年級(jí)上冊(cè)《一次函數(shù)的圖像》第2課時(shí).

一、難點(diǎn)分析

本節(jié)課是學(xué)生在了解一次函數(shù)的圖像是一條直線，并且能夠用兩點(diǎn)法畫一次函數(shù)的圖像后的繼續(xù)研究.通過本節(jié)課的學(xué)習(xí)，學(xué)生將掌握一次函數(shù)y=kx+b的圖像的性質(zhì)，以及圖像的性質(zhì)與關(guān)系式中k與b的對(duì)應(yīng)關(guān)系.

1.對(duì)本節(jié)課的難點(diǎn)的認(rèn)識(shí)

對(duì)一次函數(shù)圖像的性質(zhì)的認(rèn)識(shí)與理解是本節(jié)課的學(xué)習(xí)重點(diǎn).相對(duì)而言，一次函數(shù)關(guān)系式中k與b所決定的圖像的性質(zhì)的直觀表現(xiàn)，學(xué)生通過畫圖不難觀察發(fā)現(xiàn).比如，大多數(shù)學(xué)生通過自己動(dòng)手畫圖能作出這樣的猜想：當(dāng)k＞0時(shí)，一次函數(shù)的圖像形如“／”；當(dāng)k＜0時(shí)，一次函數(shù)的圖像形如“”.這個(gè)合情推理經(jīng)過驗(yàn)證之后，基本上能夠被學(xué)生很好地接受.但是，學(xué)生能通過畫圖歸納得到的往往是k、b與圖像直觀上的對(duì)應(yīng).學(xué)生對(duì)“y隨著x的增大而增大”“y隨著x的增大而減小”這兩個(gè)抽象語句的理解卻普遍存在困難.也就是說，學(xué)生對(duì)k所決定的“形”與“數(shù)”兩方面特征的對(duì)應(yīng)關(guān)系缺乏本質(zhì)認(rèn)識(shí).這是本節(jié)內(nèi)容在以往的教學(xué)中給筆者留下的最深的印象.基于這樣的認(rèn)識(shí)，筆者認(rèn)為本節(jié)課的學(xué)習(xí)重點(diǎn)是讓學(xué)生通過畫圖歸納得到圖像的性質(zhì)，教學(xué)的難點(diǎn)則在于幫助學(xué)生從“形”與“數(shù)”兩個(gè)方面認(rèn)識(shí)一次函數(shù)的性質(zhì).

2.尋求突破難點(diǎn)的有效方法

為什么學(xué)生在本節(jié)課的學(xué)習(xí)中會(huì)存在上述難點(diǎn)？筆者認(rèn)為，函數(shù)的圖像對(duì)于學(xué)生來說本身就具有較強(qiáng)的抽象性，在此基礎(chǔ)上進(jìn)一步研究抽象的兩個(gè)變量的對(duì)應(yīng)變化關(guān)系，對(duì)于學(xué)生來說，難度就更大了.

學(xué)生在本節(jié)課之前除了學(xué)習(xí)過一次函數(shù)的定義之外，還學(xué)習(xí)了“函數(shù)”“函數(shù)的圖像”.筆者發(fā)現(xiàn)，雖然學(xué)生對(duì)函數(shù)與函數(shù)的圖像這兩個(gè)概念都只是初步認(rèn)識(shí)，但是，學(xué)生對(duì)于一些氣溫與時(shí)間對(duì)應(yīng)關(guān)系之類的統(tǒng)計(jì)圖往往都能夠解讀到位.為了證實(shí)這一點(diǎn)，筆者在自己所在學(xué)校的八年級(jí)學(xué)生中作了調(diào)研，給學(xué)生如下圖形（如圖1）.基本上所有的學(xué)生都能找出每一時(shí)刻對(duì)應(yīng)的氣溫值，并且能說出“3時(shí)至15時(shí)氣溫逐漸升高，15時(shí)以后氣溫逐漸降低”.然而，到了一次函數(shù)的圖像中，學(xué)生就很難理解“y隨x的增大而增大”“y隨x的增大而減少”這樣的性質(zhì)，這是為什么呢？筆者認(rèn)為，上述氣溫與時(shí)間的關(guān)系圖像，雖然其實(shí)質(zhì)結(jié)構(gòu)與一次函數(shù)的圖像是一致的，但是學(xué)生從小學(xué)開始就在“統(tǒng)計(jì)”內(nèi)容中開始接觸它，相對(duì)來說較為熟悉.另外，圖中的兩個(gè)維度的變量都限于非負(fù)實(shí)數(shù)范圍內(nèi)，并且具有明確的現(xiàn)實(shí)意義，抽象度較低，學(xué)生容易通過聯(lián)系現(xiàn)實(shí)生活來理解它.相反，本節(jié)課在整個(gè)實(shí)數(shù)范圍內(nèi)研究的一次函數(shù)中的兩個(gè)變量，完全以抽象形式存在，缺乏具體的現(xiàn)實(shí)意義，理解起來就很困難了.

圖1

圖2

圖3

蘇科版教材中采用了如圖2所示的現(xiàn)實(shí)情境來幫助學(xué)生理解這一點(diǎn).這個(gè)情境以一個(gè)山峰的兩側(cè)來幫助學(xué)生理解“從左向右，越來越高”“從左向右，越來越低”.筆者認(rèn)為，這個(gè)情境向?qū)W生呈現(xiàn)的其實(shí)仍然只是直觀與形式上的特點(diǎn)，對(duì)于數(shù)與形對(duì)應(yīng)關(guān)系的理解沒有起到很好的鋪墊作用.相反，如果用上述氣溫與時(shí)間變化關(guān)系的圖像則更容易被學(xué)生理解和接受，從它發(fā)展到“y隨x的增大而增大”或“y隨x的增大而減小”，跨度明顯縮小.但是，筆者隨后發(fā)現(xiàn)，上述溫度與時(shí)間的關(guān)系圖像中橫坐標(biāo)從左向右如果理解為“時(shí)間的增大”顯得有些牽強(qiáng).于是，這里需要一個(gè)更為合適的導(dǎo)例.這時(shí)，筆者突然想到了之前在網(wǎng)上曾經(jīng)看過人的液態(tài)智力與年齡的關(guān)系圖像（如圖3）.筆者發(fā)現(xiàn)，如果用這個(gè)圖像作為本節(jié)課的導(dǎo)例，可以成為一個(gè)很好的“生長(zhǎng)點(diǎn)”，通過對(duì)它進(jìn)一步抽象來幫助學(xué)生理解一次函數(shù)的圖像的性質(zhì).

到此，筆者對(duì)于本課的難點(diǎn)突破有了清晰的思路：先利用學(xué)生對(duì)統(tǒng)計(jì)圖的認(rèn)識(shí)經(jīng)驗(yàn)來理解具有明確現(xiàn)實(shí)意義的函數(shù)圖像的性質(zhì)，在此基礎(chǔ)上擺脫現(xiàn)實(shí)意義，提高抽象度，將這種認(rèn)識(shí)自然過渡到一次函數(shù)的圖像上來.有了這樣的思路之后，備課就很快完成了.

二、課堂片斷回放

片斷1

教師：同學(xué)們，老師昨天在網(wǎng)上看到了一篇文章之后，得出這樣的一個(gè)結(jié)論：同學(xué)們是越來越聰明了，而老師則是越來越笨了！

（學(xué)生們聽了這番話之后很詫異）

（這時(shí)，利用PPT向?qū)W生呈現(xiàn)圖3，配有這樣一段文字：科學(xué)研究發(fā)展，人的智力（液態(tài)智力，主要包括運(yùn)算力、記憶力、思維的敏捷性等）與人的年齡存在如圖3所示的關(guān)系）

教師：請(qǐng)同學(xué)們就這個(gè)圖相互交流一下，說說你從這個(gè)圖中獲得了哪些信息，你覺得老師剛才的“感慨”是否有道理呢？

（學(xué)生的好奇心被激發(fā)起來）

學(xué)生1：從圖中可以看出，人的智力水平在20歲之前隨著年齡的增長(zhǎng)而上升，20歲到30歲之間變化不明顯，而到30歲以后，智力則隨著年齡的增長(zhǎng)而下降.

學(xué)生2：老師，您剛才說的話是有道理的，因?yàn)槲覀兡挲g處于智力上升的那一段，而您則處于智力下降的那一段.

（其他學(xué)生紛紛點(diǎn)頭贊同學(xué)生2的說法）

教師：這句話說得好，“隨著年齡的增長(zhǎng)而上升”，在這個(gè)圖中，如果我們分別用x來表示年齡，用y來表示智力水平，那么這句話是否可以換一種說法？

（PPT中隱去了“智力”與“年齡”，分別替換為y和x）

學(xué)生3：那么20歲之前與30歲之后這兩段分別可以說成是y隨著x的增大而增大，y隨著x的增大而減小.

教師：我們已經(jīng)知道一次函數(shù)的圖像是一條直線，那么它是否也存在類似的特點(diǎn)呢？這樣的特點(diǎn)與函數(shù)的關(guān)系式是否存在著什么聯(lián)系呢？大家動(dòng)手畫兩個(gè)一次函數(shù)的圖像，對(duì)比它們的函數(shù)關(guān)系式與圖像，說說你的發(fā)現(xiàn).

（學(xué)生動(dòng)手畫圖，教師也在黑板上畫圖，幾分鐘后，學(xué)生們開始在小組內(nèi)交換各自的發(fā)現(xiàn)）

學(xué)生4：老師，我發(fā)現(xiàn)當(dāng)k＞0時(shí)直線是向上的，當(dāng)k＜0時(shí)直線是向下的.

教師：“向上”？“向下”？（指著黑板上的兩條直線）這兩根線都有向上啊！

學(xué)生4：我指的是k＞0時(shí)，圖像從左向右看是向上的，k＜0時(shí)，從左向右看是向下的.

教師：這個(gè)表達(dá)不錯(cuò)！“從左向右看，是向上的”.其他同學(xué)是否有不同的看法，或者有不同于他的表達(dá)？

學(xué)生5：老師，我覺得應(yīng)當(dāng)說k＞0時(shí)y隨著x的增大而增大；k＜0時(shí)y隨著x的增大而減小.

教師：不錯(cuò)，又是一種說法，有沒有不同意見？

（無人舉手）

教師：學(xué)生4和學(xué)生5分別給出兩種不同說法，究竟誰對(duì)誰錯(cuò)？

（有些學(xué)生陷入沉思中，有不少學(xué)生立即反應(yīng)過來）

學(xué)生6：他們兩人其實(shí)是一樣的說法，從左向右看，其實(shí)就是x增大；上升，也就是y增大.

到此，本課的難點(diǎn)從一個(gè)合適的“生長(zhǎng)點(diǎn)”上得到自然的突破.

片斷2

在本節(jié)課的鞏固運(yùn)用環(huán)節(jié)，筆者設(shè)計(jì)如下練習(xí)題：

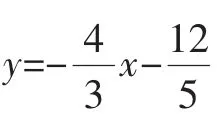
A.y1＞y2B.y1=y2C.y1＜y2D.無法確定

學(xué)生7：將兩個(gè)點(diǎn)分別代入函數(shù)關(guān)系式，求出y1與y2，就可以比較它們的大小了.

教師：不錯(cuò)，其他同學(xué)有沒有不同的方法？

（大部分學(xué)生采取與學(xué)生7相同的方法，然而學(xué)生7說完之后，立即有幾個(gè)同學(xué)舉手爭(zhēng)搶著說自己有更簡(jiǎn)單的方法）

學(xué)生8：不需要代入運(yùn)算，因?yàn)檫@里的k＜0，那么這個(gè)函數(shù)中y隨著x的增大而減小.這里－4＜2，那么y1＞y2.

（很多學(xué)生恍然大悟）

教師：很好！學(xué)到的東西立即就能運(yùn)用.這種方法的好處在于不需要進(jìn)行運(yùn)算.如果將本題作如下更改：“已知點(diǎn)（－4，y1）、（2，y2）都在直線y=mx－n（m＞0）上，則y1與y2的大小關(guān)系是（ ）”，這時(shí)，學(xué)生7的方法就很難解決問題了.實(shí)際上原題中關(guān)系式中的系數(shù)有意設(shè)置了計(jì)算上的麻煩！

（學(xué)生們會(huì)意地點(diǎn)點(diǎn)頭）

三、反思與感悟

比賽結(jié)束后，筆者以所在縣區(qū)第一名的成績(jī)進(jìn)入市級(jí)復(fù)賽.評(píng)委老師在肯定筆者的教學(xué)設(shè)計(jì)的同時(shí)，也指出了本課實(shí)施過程中的一個(gè)問題，那就是學(xué)生通過對(duì)比兩個(gè)一次函數(shù)的圖像得出結(jié)論，顯得過于匆忙.實(shí)質(zhì)上，對(duì)于圖像的性質(zhì)與k、b的對(duì)應(yīng)關(guān)系，應(yīng)當(dāng)建議學(xué)生通過變換不同的取值盡可能多次進(jìn)行畫圖觀察對(duì)比，在學(xué)生得到猜想的時(shí)候，教師應(yīng)當(dāng)提醒學(xué)生對(duì)自己的猜想作出充分的驗(yàn)證，讓學(xué)生感受到“觀察、猜想、驗(yàn)證”這樣一個(gè)數(shù)學(xué)發(fā)現(xiàn)的完整過程.這樣的過程呈現(xiàn)，不僅有助于學(xué)生形成嚴(yán)謹(jǐn)?shù)臄?shù)學(xué)態(tài)度，更有利于獲得更為深刻的認(rèn)識(shí).比如，學(xué)生通過不同k的取值驗(yàn)證，不僅能驗(yàn)證圖像的性質(zhì)與k的對(duì)應(yīng)關(guān)系，還有可能發(fā)現(xiàn)k的絕對(duì)值的大小與圖像的特點(diǎn)的對(duì)應(yīng).這一點(diǎn)，筆者在課后也意識(shí)到了，反思自己的課堂，我覺得自己很多時(shí)候急于達(dá)成預(yù)設(shè)的目標(biāo)，一旦學(xué)生的回答契合預(yù)設(shè)，就立即轉(zhuǎn)入下一環(huán)節(jié).其實(shí)，很多時(shí)候恰恰是我們過于匆忙，沒能讓學(xué)生的思維更深刻些，沒給學(xué)生發(fā)現(xiàn)更多問題、提出更多問題的時(shí)間和空間.

另外，筆者在這次活動(dòng)之后還對(duì)一節(jié)課的難點(diǎn)的突破有所感悟.我們常常將教學(xué)思維集中在新知的處理上，而忽視對(duì)學(xué)生現(xiàn)有知識(shí)經(jīng)驗(yàn)的充分挖掘.在追求“跳一跳，夠得到”這個(gè)教學(xué)效果的時(shí)候，我們常常花過多的心思去“壓低枝頭的果實(shí)”，而忘了幫助學(xué)生找到一個(gè)最合適的“起跳點(diǎn)”！顯然，從“學(xué)會(huì)學(xué)習(xí)”和學(xué)生長(zhǎng)遠(yuǎn)發(fā)展的角度來看，后者具有更高的現(xiàn)實(shí)意義，因?yàn)閷砀嗟臅r(shí)候，學(xué)生將獨(dú)自面對(duì)“枝頭的果實(shí)”.事實(shí)上，在學(xué)生的認(rèn)知結(jié)構(gòu)中，總是存在著一個(gè)離新知最近的點(diǎn)，在那個(gè)點(diǎn)上著力，新知的建構(gòu)會(huì)變得容易許多！教師要做的，就是善于引導(dǎo)學(xué)生利用現(xiàn)有認(rèn)知，在類比中實(shí)現(xiàn)遷移，讓新知自然生長(zhǎng)！