基于LabVIEW的電機振動信號分析

鄒世明 張祥明

( 井岡山大學 機電工程學院，江西 吉安 343009)

1 LabVIEW 簡述

LabVIEW 是美國NI 研發的一種基于G 語言的圖形編程開發環境，是一種用圖標代替文本行創建應用程序的圖形化編程語言。用該種方式開發完成的程序，其構成文件大部分都是后綴名為vi 的文件，這些文件因其后綴而被叫做VI。VI文件一般有四個組成部分:首先是前面板，前面板主要的功能是交互，將使用者輸入的數據和指令輸送給另一個組成部分框圖，而計算和分析結果也在前面板上以數字、圖形或是表格等各式各樣的方式表現出來。其次是框圖部分，該部分中主要是負責將前面板接到的指令進行計算，然后將最終的計算結果傳輸給使用者。還有就是圖標，圖標是VI 文件的外在的圖形符號，LabVIEW 為了滿足使用者對圖標的不同喜好，專門設置了圖標編輯器，從而讓使用者們能夠自主的制作自己所欣賞的圖標。最后的一個組成部分則是連線板，該部分是自定義輸入和輸出。以上四個部分共同組成了VI 文件，在彼此的相互配合下，使該文件的功能得到良好發揮。

2 振動信號的時域分析

常見的反映振動信號的基本特征參數有:均值μ、均方根Xrms、峰峰值φx。均值反映信號的靜態分量，即常值分量。均方根也稱作為有效值，它的計算方法是先平方、再平均、然后開方。峰峰值主要是針對周期穩態信號而言，對于隨機信號無法確定。

(1)均值

振動信號的均值是樣本函數x(k)在整個時間坐標上的積分平均，其物理含義為該振動信號變化的中心趨勢，離散振動信號均值計算公式為

(2)均方根

振動信號的均方根是為信號的有效值，離散振動信號均方根計算公式如下:

(3)峰峰值

振動信號的峰峰值是信號最高正峰max{x(k)}到最低負峰min{x(k)}的距離，離散振動信號峰峰值計算公式為φx=max{x(k)}－min{x(k)}。

3 振動信號的頻域分析

傅立葉變換作為平穩信號分析、處理的一項關鍵技術，能夠將一個時域的問題通過傅立葉變換能轉化成頻域的問題來分析研究。設x(t)為t 的函數，并且滿足狄氏條件，具體的計算式如下:X(f)=∫+∞－∞x(t)e－2πftdt。

連續傅立葉變換實現了測試信號從時域到頻域的轉換，在理論分析中具有很大的價值。雖然其功能強大，但是連續傅立葉變換也有自身的不足之處，它不能直接使用在計算機技術上，因為繁瑣的計算限制了它的進一步發展。這種情況的改善是源于離散傅立葉變換的出現，離散傅里葉變換讓數學方法與計算機技術進行了很好的融合，兩者的融合使得工程的發展有了更大的保障依據。設x(k)為一時域數字序列，具體的計算方式如下

對于離散傅立葉變換，求出N 點x(k)需要N2次復數乘法，N(N－1)次加法運算。每次復數乘法要做四次實數乘法，兩次實數加法運算。這樣當N 很大時，所需的計算工作量也是相當可觀的。為了進一步減少計算量，庫利－圖基于1965年提出了快速傅立葉算法，使用快速傅立葉變換，計算N 點離散傅立葉的計算量由N2次復數乘法降為Nlog2N 次復數乘法，計算強度明顯降低。

4 電機振動信號檢測分析

電機振動信號的由速度傳感器檢測電動機振動信號，從速度傳感器檢測到的電機振信號往往比較小，易受噪聲影響，在用數據采集卡采集前，先要將微弱信號放大預處理，然后再利用數據采集卡進行數據采集，利用LabVIEW 中的分析函數和功能模塊對特征信號值進行數字濾波以及進一步的分析處理，采用一定機制方法，如值域判定、時域判定、幅度譜判定、相位譜判定、功能判定和邏輯判定等作出評判，最后實現電機的健康診斷。當然由LabVIEW 軟件開發完成的工作有數據采集、信號處理、健康診斷。其檢測分析具體過程見圖1 所示。

圖1 振動信號檢測分析框圖

我們根據電機在正常運轉時所產生的震動和噪聲，對檢測處得振動信號進行詳細全面的檢測，由于電機工作時要經歷啟動、加速、勻速、減速到停止各個工作階段，為便于對電機的狀態分析，對其勻速運轉階段的振動信號進行分析。其振動信號時域波形和頻譜分析圖如圖2、圖3 所示:

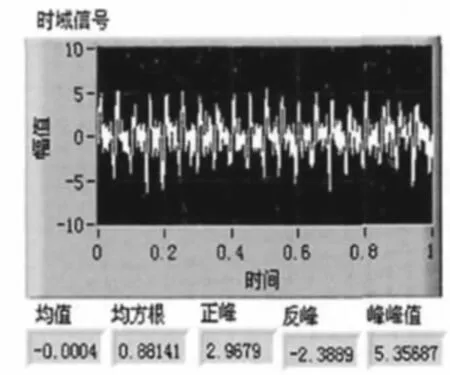
圖2 振動信號時域波形

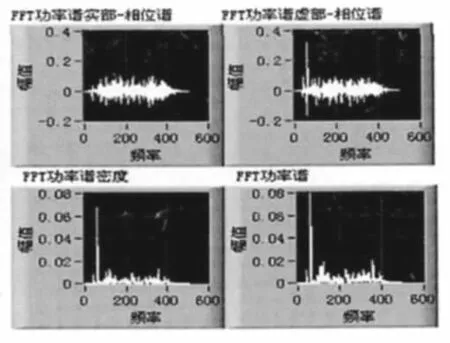
圖3 頻譜分析圖

5 結論

LabVIEW 提供了豐富的圖形化的編程方法，在設計具體的系統過程中可以徹底的從復雜枯燥的編程工作中解放出來，而不需要用大量的精力去搭建實驗系統設備，完成工程設計與應用的效率有了大大的提高。本文將虛擬儀器技術與電機信號檢測技術相結合。研究了基于LabVIEW 的電機振動信號檢測的方法，通過具體的應用測試，驗證了該系統的實用性與高效性。

［1］張桐，陳國順，王正林編著.精通LabVIEW 程序設計［M］.北京:電子工業出版社，2008.

［2］楊樂平等.LabVIEW 高級程序設計［M］.北京:清華大學出版社，2003.