大學物理中多普勒效應的教學體會

章 敏

(安徽建筑大學 數理系，安徽 合肥 230022)

1 經典多普勒效應

1.1 波源靜止，觀測者運動

波在介質的速度為u，波源靜止，觀測者在介質的速度為v觀，波相對于觀測者的速度為u+v觀，觀測者接收的頻率為

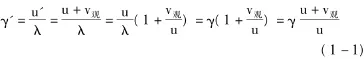
1.2 波源運動，觀測者靜止

波在介質的速度為u，但由于波源的運動，波長速短了λ-v源T。具體解釋如下：當波源靜止時，前后相鄰兩個等相面間的距離為λ，但當波源運動時，前一個等相面自波源出發后，就以速度v源行進，在后一個等相面自波源出發時，波源已向前移動了v源T，這時兩個等相面間的距離為λ-v源T，及波長變為λ-v源T。觀測者接收的頻率為

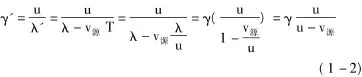
1.3 波源運動，觀測者運動

如果波源和觀測者遠動方向在同一直線上，結合前兩者的結論，觀測者接收的頻率為

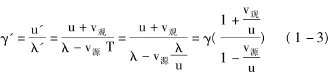
如果波源和觀測者遠動方向不在同一直線上，那么情況更加復雜。可以將波源和觀測者速度沿著某一方向進行分解，波源和觀測者速度在這個方向上的夾角分別是α和β，觀測者接收的頻率為

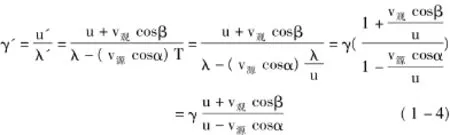
對該結論進行討論可得出以下結果：1)v源和v觀在連線上運動，α=0，β=0，(1-4)式即化簡為(1-3)式，即所說的縱向多普勒效應。而一般情況下v源和v觀不變，α，β是隨時間變化的，因此，γ'是時間的函數。2)當 u=v源，γ'=γ

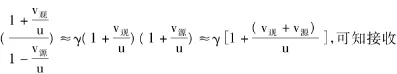
的頻率與源與觀測者的相對速度有關。

2 相對論多普勒效應

電磁波的速度在相同環境下傳播速度是相同的，電磁波的傳播速度等于光速，即γλ=c。對不同的參考系測得的波的頻率和波長的乘積相同但頻率和波長卻不同。

我們取相對光源靜止的參考系為S系，相對于觀察者靜止的參考系為S'系，如圖。設光源位于S系的O點上，S系相對于S'系以速度v沿x正方向運動。相對于S系，在某一時刻t，光源發出某一相位的等相面，經過時間光源又發出同一相位的等相面，用相對論語言就是：在S系的O點處，發生了兩個事件，且時間間隔為如圖。

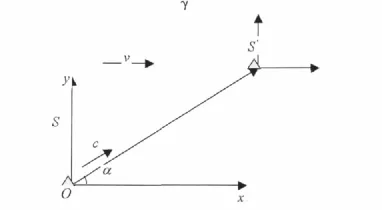
對于S'系：第一個等相面發出的時刻為

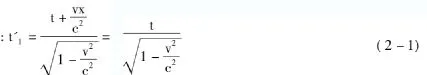
第二個等相面發出的時刻為

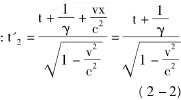
第一個等相面發出的坐標為

第二個等相面發出的時刻為：

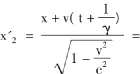
因此，兩個等相面的時間間隔為：

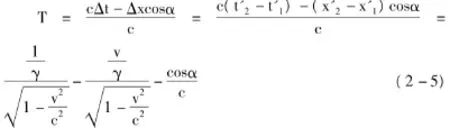
則觀察者接收的頻率為：

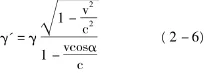
對該結論進行討論可得出以下結果：1)觀測者在相對運動方向上，即即所說的縱向多普勒效應。2)觀測者垂直于相對運動方向上，即即所說的橫向多普勒效應。3)相對論多普勒效應只與源與觀測者相對運動有關。4)當與經典情況下的結論一致，所以經典理論和與相對論理論解釋多普勒效應是自洽的。

3 結語

綜上所述，運用經典理論和相對論理論，得出多普勒效應的兩種不同表達形式。通過分析可得出以下結論：1.經典多普勒效應與源運動和觀測者運動都有關，且后兩者運動產生多普勒效應的機制也不同;而相對論多普勒效應只與源與觀測者相對運動有關。2.在經典多普勒效應中，只考慮縱向多普勒效應;而相對論多普勒效應，不僅有縱向多普勒效應，也有橫向多普勒效應。3.兩種理論分別適用于多普勒效應的低速源、高速源，在極端情況下，兩者的結論是一致的。

[1]程守洙等，普通物理學[M].北京：高等教育出版社，2006.

[2]張三慧等，大學物理學[M].北京：清華大學出版社，1999.

[3]顧建中，普通物理學簡明教程[M].北京：人民教育出版社，1977.

[4]楊仲耆，大學物理學[M].北京：高等教育出版社，1981.