巧構輔助函數證明微分中值定理
2013-08-14 05:27:50呂端良王云麗
河南科技 2013年11期
呂端良 王云麗
(山東科技大學 泰安校區,山東 泰安 271000)
高等數學中微分中值定理的證明方法比較多,本文受高等數學(同濟五版)P132頁第13題啟發,通過構造一個三階行列式輔助函數,應用Rolle微分中值定理,證明了Lagrangge微分中值定理和Cauchy微分中值定理。
定理 設函數f(x)、g(x)、h(x)在閉區間[a,b]上連續,在開區間(a,b)內可導,則在區間(a,b)內至少存在一點 ζ,使得

則有該函數在閉區間[a,b]上連續,在開區間(a,b)內可導,且根據行列式的性質得
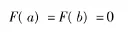
所以函數F(x)在區間[a,b]上滿足Rolle微分中值定理的條件,故由Rolle微分中值定理知,在區間(a,b)內至少存在一點 ζ,使得 F'(ζ)=0
又根據行列式的性質及求導公式得F'(x)=

推論1.(Lagrange微分中值定理) 設函數f(x)在閉區間[a,b]上連續,在開區間(a,b)內可導,則在區間(a,b)內至少存在一點ζ使得
證明 構造輔助函數,在定理1證明中的輔助函數F(x)里,令g(x)=x、h(x)=1,該定理就得到了證明。
推論2.(Cauchy微分中值定理) 設函數f(x)、g(x)在閉區間[a,b]上連續,在開區間(a,b)內可導,則在區間(a,b)內至少存在一點ζ,使得
證明 構造輔助函數,在定理1證明中的輔助函數F(x)里,令h(x)=1,該定理就得到了證明。
[1]同濟大學應用數學系.《高等數學》.高等教育出版社.2011.5

