催化裂化原料特性因子的計算

程 從 禮

（中國石化石油化工科學研究院，北京 100083）

特性因數K常用于劃分石油和石油餾分的化學組成，在評價催化裂化原料的質量上被普遍使用。特性因數K值又稱Watson K值或UOP K值［1］，是油品平均沸點和相對密度的函數，其具體的關系式如下：

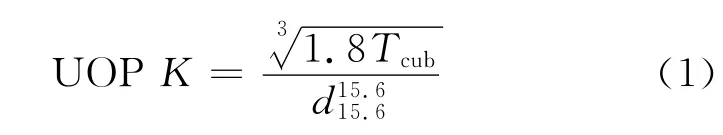
式（1）中，Tcub為立方平均沸點，K；為15.6℃時油品的密度與水的密度的比值。

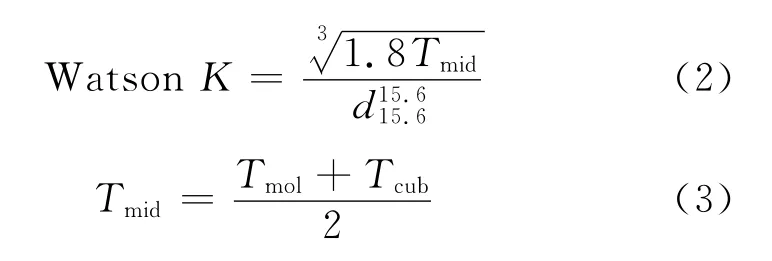
式（2）中，Tmid為中平均沸點，K；Tmol為分子平均沸點，K。

特性因數是一種說明催化裂化原料中石蠟烴含量的指標。K值高，原料的石蠟烴含量高；K值低，原料的石蠟烴含量低。但K值在芳烴和環烷烴之間則不能被有效區分。烷烴的K值最大，約為12.7；環烷烴的K值次之，為11～12；芳烴的K值最小，為10～11。原料特性因數K值的高低最能說明該原料的生焦傾向和裂化性能。原料的K值越高，就越易于進行裂化反應，而且生焦傾向也越小；反之，原料的K值越低，就越難于進行裂化反應，而且生焦傾向也越大。所以K值是表征油品化學組成的重要參數，常可用于關聯其它物理性質。但對于含有大量烯烴、二烯烴和芳烴的二次加工產物，特性因數并不能準確地表征其化學屬性，使用時會導致較大的誤差［2－4］。

特性因數的計算方法有兩種：一是依據餾程和密度的分析數據，由公式（1）和公式（2）再結合諾謨圖查圖計算；二是根據相對分子質量和密度的數據由經驗關聯式計算。由于在日常生產過程中，對原料通常只進行密度、殘炭以及餾程等常規項目的分析，給催化裂化特性因數K值的計算帶來困難。

本課題從催化裂化工業裝置原料的日常分析數據（通常只有密度、殘炭以及餾程）出發，提出催化裂化原料特性因素的計算式，以便于科研、設計及生產部門快速準確地了解裝置所加工原料的性質。

1 基于餾程和密度的特性因數計算方法

根據餾程分析數據，按照式（4）計算體積平均沸點tvol。

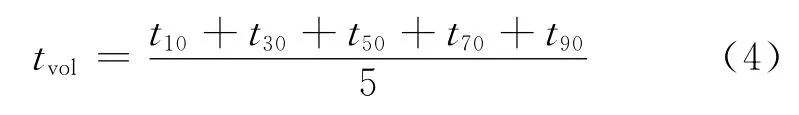
式（4）中，t10，t30，t50，t70，t90分別表示餾出體積分數為10%，30%，50%，70%，90% 時 的 餾 出 溫度，℃。

由式（5）計算餾程曲線的斜率。

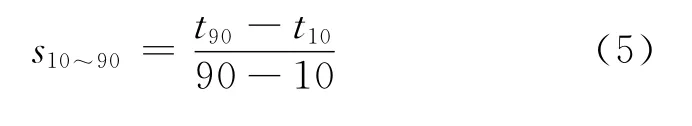
根據式（4）計算出體積平均沸點tvol后，采用諾謨圖，由10%～90%餾程直線斜率s10～90查出該斜率所對應的相對于體積平均沸點的校正值tcal，然后按照式（6）計算平均沸點。

式（6）中，ti是泛指平均沸點，可以分別表示分子平均沸點、中平均沸點、立方平均沸點或質量平均沸點，℃。

由式（1）和式（2）可知，要計算特性因數 K值，關鍵是求出平均沸點。雖然由餾程數據得到10%～90%餾程直線斜率后可以查閱諾謨圖得到各平均沸點的校正值，但是該方法并不方便，尤其在編制催化裂化計算模擬軟件時不利于計算機自動處理。為此，根據諾謨圖中的曲線提出如式（7）所示的計算體積平均沸點校正值tcal的關系式。

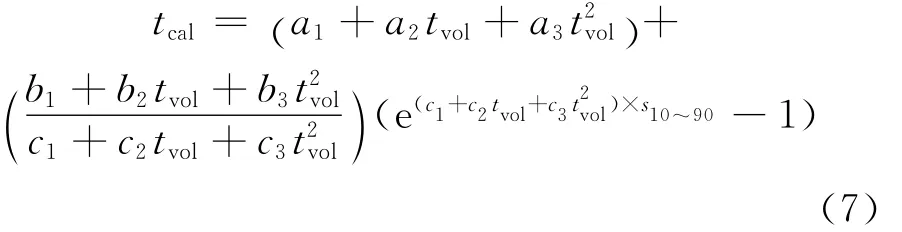
由式（7）可見，平均沸點的校正值被關聯成體積平均沸點和10%～90%餾程直線斜率的函數。式（7）中a，b，c等參數表示校正系數，對于不同的平均沸點其值不同，其具體數值可以從諾謨圖中的數據關聯得到，分別列于表1。

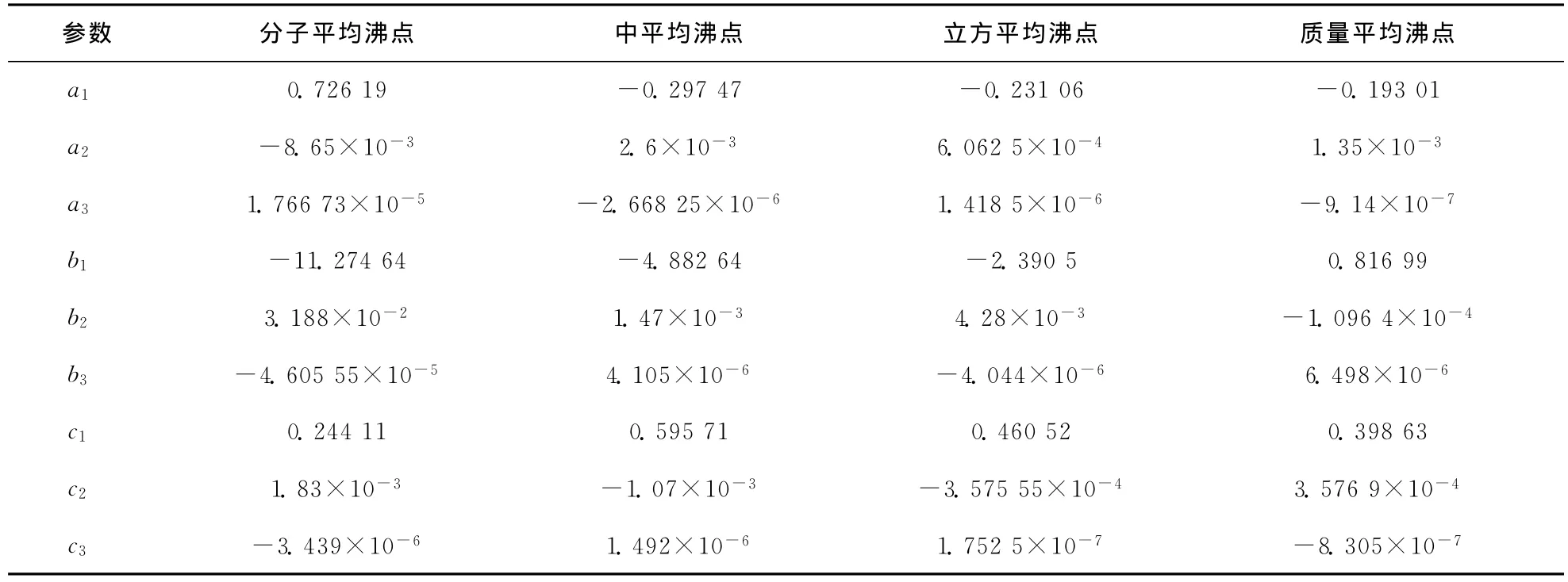
表1 平均沸點校正系數

通過一個實例對平均沸點的計算進行驗證，表2為原料餾程，表3為平均沸點驗證結果。由表3可見，式（6）和式（7）的計算精度較高，相對誤差小于1.5%。

表2 原料餾程

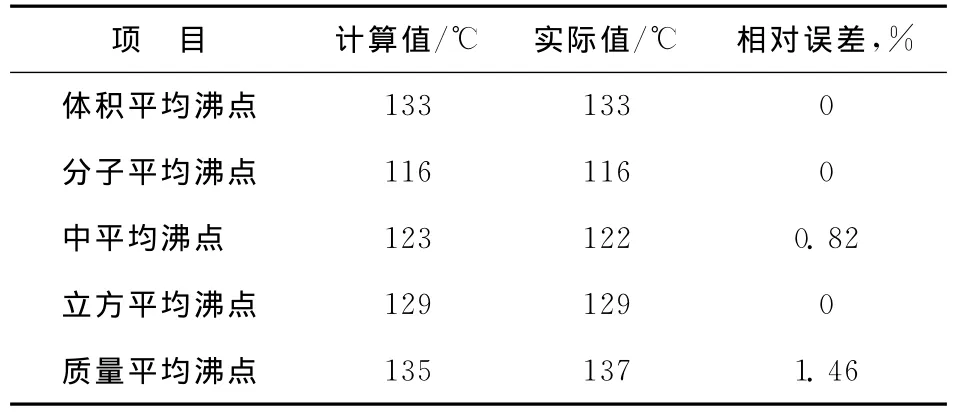
表3 由式（7）計算得到的原料平均沸點結果

根據原料的餾程數據，由式（6）、式（7）可以計算出平均沸點，對于UOP K值，選擇立方平均沸點，對于Watson K值選擇中平均沸點。計算特性因數K值時，除了平均沸點之外，還需要原料的密度。通常煉油廠分析數據提供的是20℃的密度，而特性因數K值需要15.6℃（即60℉）條件下的密度，為此需要將20℃的密度換算成15.6℃的密度。

原料的密度與溫度有著密切的關系，根據不同溫度下的原料密度數據［5］，關聯出原料密度與溫度的變化關系式：

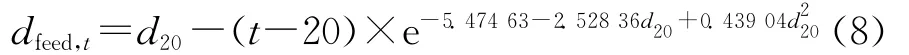
式（8）中，t表示溫度，℃；dfeed表示原料的密度，g／cm3。

以某MIP裝置的原料性質標定值為例，利用上述計算式對該原料的特性因數進行計算，結果見表4。由表4可見，計算出的UOP K值為11.74，Watson K值為11.72，二者十分接近。由此可見，該原料油可定性為環烷基原料油。

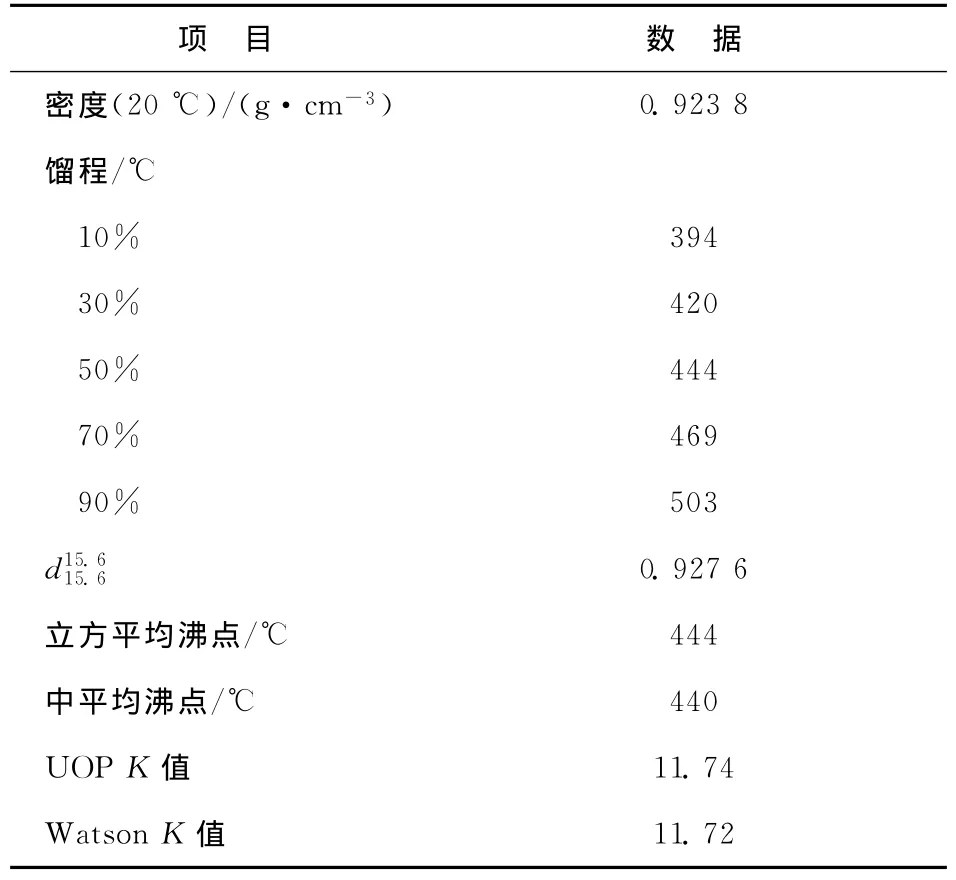
表4 某MIP裝置的原料性質及特性因數計算值

2 基于10%餾出溫度和密度的特性因數計算方法

根據式（1）或式（2）的特性因子計算式，已知原料的密度和平均沸點就可以計算出特性因子。由于催化裂化原料通常密度較大，大多數情況下并不能得到完整的餾程數據。文獻［2］報道用原料的平均相對分子質量和20℃下的相對密度對立方平均沸點進行計算，如式（9）所示。

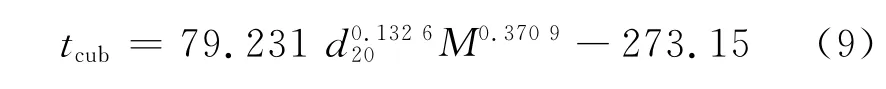
式（9）中，M表示原料的平均相對分子質量。

利用式（9）計算原料的立方平均沸點時，需要原料的平均相對分子質量測量值，該值在煉油廠催化裂化裝置日常生產分析中幾乎不進行測試，所以式（9）的應用受到限制。但是，在煉油廠催化裂化原料的常規分析項目中，可以得到10%餾出體積時的溫度。本課題由原料的密度和10%餾出體積下的溫度（t10）回歸出立方平均沸點的計算式，進而根據式（1）計算特性因子UOP K值。立方平均沸點的計算式如式（10）所示。

根據11套催化裂化裝置的原料數據，采用式（7）、式（9）以及式（10）進行立方平均沸點計算并進行比較，結果見表5。

表5中立方平均沸點的實測值指的是利用式（7）計算得到的結果，因為該值與諾謨圖查得的值非常接近。如果取相對誤差的絕對值，式（10）的平均相對誤差為1.59%，而式（9）的平均相對誤差為2.89%。從相對誤差絕對值的范圍來看，式（10）的相對誤差絕對值在0.04%～3.56%之間，而式（9）的相對誤差絕對值范圍則為0.97%～5.76%。由此可見，在不能得到完整的餾程數據時，本課題提出的計算式（10）的精度高于式（9）。

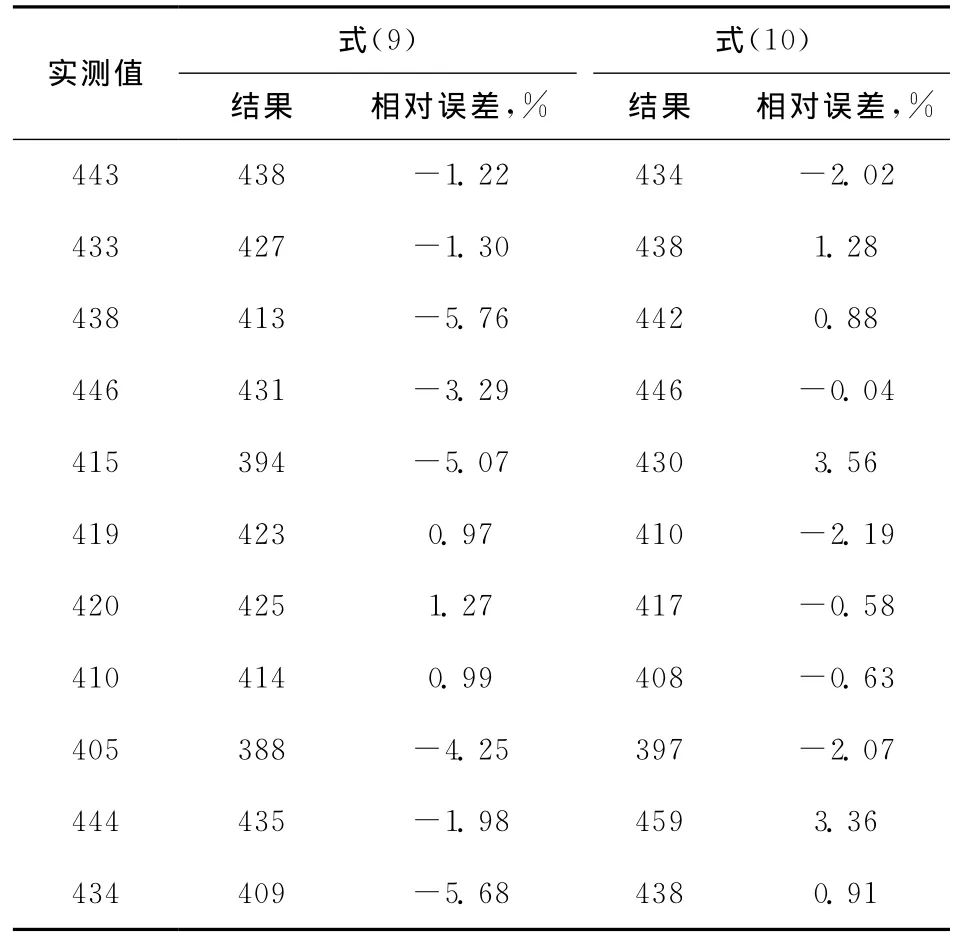
表5 不同方法得到的催化裂化原料的立方平均沸點計算結果

3 結 論

（1）根據諾謨圖的數據關聯出質量平均沸點、分子平均沸點、立方平均沸點和中平均沸點的計算式。計算結果與諾謨圖的數值非常接近，在已知原料完整餾程的條件下，完全可以替代諾謨圖。

（2）根據原料密度以及10%餾出體積時的溫度關聯出分子平均沸點的關系式，用于計算特性因子UOP K值。該關聯式的計算結果與實際值的相對誤差小于4%。

（3）提出了原料密度與溫度的關系式，該關系式不僅可用于特性因數的計算，而且可用于催化裂化工業裝置標定時原料流量的快速計算。

［1］US－ASTM.UOP Method 375—2007.Calculation of UOP characterization factor and estimation of molecular weight of petroleum oil［S］.2007：1－14

［2］陳俊武.催化裂化工藝與工程［M］.2版.北京：中國石化出版社，2005：400－488

［3］曹漢昌，郝希仁，張韓.催化裂化工藝計算與技術分析［M］.北京：石油工業出版社，2000：33－60

［4］林世雄.石油煉制工程［M］.3版.北京：石油工業出版社，2000：63－107

［5］梁文杰.石油化學［M］.北京：石油大學出版社，1995：98－102