平板耦合顫振過程中氣動能量轉換特性

劉祖軍，楊詠昕，葛耀君

(1.華北水利水電學院 土木與交通學院，鄭州 450011;2.同濟大學 橋梁工程系，上海 200092)

橋梁顫振是由于氣動不穩定性引起的一種自激發散振動，該振動現象一旦發生，將導致橋梁結構整體的毀滅性破壞。因此大跨度橋梁結構顫振問題的研究顯得非常重要。目前橋梁顫振機理的研究包括橋梁顫振理論和驅動機理、顫振分析方法和橋梁斷面氣動性能等諸多方面。國內外眾多學者針對這些研究內容展開了深入的研究。

Matsumoto用一種Step-by-step方法即分步分析的方法對不同寬高比的矩形斷面以及菱形、橢圓形、三角形等斷面的氣動導數和氣動阻尼進行了風洞試驗和理論研究［1-3］，并將斷面顫振按機理區分為四類:即耦合顫振、高速顫振、低速顫振和限速顫振。

楊詠昕等［4-6］在Matsumoto研究思路的基礎上，導出了二維三自由度耦合顫振分析方法，用該方法對平板，橋梁斷面和一些氣動措施的顫振機理進行了研究。通過分析他指出，理想薄平板的經典耦合扭彎顫振是由扭轉主運動位移所產生的氣動升力激發起耦合豎向振動，耦合豎向運動的速度產生的耦合氣動升力矩又反饋作用到扭轉主運動上的這樣一條激勵-反饋路線是導致系統發散的主線。

Scanlan等［7］最早建立了橋梁顫振的多模態分析方法，并從能量觀點對橋梁的顫振穩定性進行了很有價值的研究，給出了在一個振動周期內氣流沿橋梁斷面每延米輸入的總能量和結構耗能的表達式，并闡述了氣流輸入到結構中的能量不僅與彎扭位移的幅值有關，而且與彎扭位移間的相位差有著密切的關系，但是他在能量部分僅給出了一個理論框架，沒給出具體方法。

劉高［8］從結構與氣流系統內部能量平衡的觀點對系統的顫振進行研究，發展了一種全橋多模態顫振能量分析方法，通過建立系統等效阻尼比與系統能量變化率之間的關系，推演了系統以及各階模態等效阻尼比的計算方法，并根據不同風速下系統能量變化率來判斷系統的顫振穩定性。

本文應用激勵-反饋的分步分析方法對耦合顫振方程進行解耦，并將耦合顫振運動方程改造為能量方程形式，通過引入考慮阻尼影響的運動方程形式，建立了結構-氣流系統顫振能量機理的研究框架，詳細推導了振動系統內部作用力輸入到系統振動能量的計算方法，結合平板風洞試驗對比分析了顫振前和顫振臨界狀態下系統主要氣動力的能量輸入和轉換特性，研究了影響氣動能量輸入的主要因素，從能量轉換的角度對平板彎扭耦合顫振進行了分析。

1 耦合顫振能量轉換分析框架

1.1 耦合顫振能量方程的建立

在僅考慮自激力作用情況下，具有豎彎和扭轉兩個自由度的橋梁斷面(圖1)在空氣中的運動方程［9］可以寫為:

根據二維耦合顫振分析理論，應用分步分析思路建立了如圖2所示的耦合顫振能量分析框架。

考慮到扭轉振動中含有豎向振動的頻率成分ωh，豎向振動中也含有扭轉振動的頻率成分ωa，因此假設扭轉振動和豎向振動均有兩種振動頻率成分的參與，故扭轉和豎向振動可表示為下式:

圖1 二維橋梁節段Fig.1 Two dimensional bridge-girder section

圖2 耦合顫振能量分析框架Fig.2 The energy analysis framework of coupled flutter

其中:α0(t)是振動頻率為ωa的扭轉運動，α1(t)是豎向運動激發的振動頻率為ωh的扭轉運動;h0(t)是振動頻率為ωh的豎向運動，h1(t)是扭轉運動激發的振動頻率為ωa的豎向運動。

假設扭轉主運動α0(t)和豎向主運動h0(t)的方程表達式如下:

根據分步分析思路，將式(3a)代入式(1a)中求解扭轉主運動激發的豎向牽連運動h1(t):

同理將豎向主運動式(3b)代入式(1b)求解豎向主運動激發的扭轉牽連運動α1(t):

以上公式中的參數如下:

為了從能量角度考慮顫振過程中振動系統內主要氣動力對系統能量的貢獻將顫振運動控制方程改寫為能量運動方程:

將上述的分析得到的a(t)和h(t)的表達式代入式(7)就可以分析顫振過程中氣動能量轉換機理以及氣動能量的輸入特性，便于從能量角度對顫振發生機理進行探討。

1.2 扭轉系統內主要氣動力向振動系統輸入的能量

式中的參數:

式中的參數:

2 平板扭轉振動能量分析

2.1 主要氣動力的能量輸入特性

為盡可能接近理想平板，采用了寬高比為22.5的平板剛體節段模型，外形尺寸見圖3，模型基本參數如下:m=11.25 kg/m，Im=0.282 8 kg·m2/m，豎向圓頻率 ωh=12.11 rad/s，扭轉圓頻率 ωα=19.0 rad/s。平板氣動導數如圖4所示。試驗在同濟大學土木工程防災國家重點實驗室TJ-1邊界層風洞進行，顫振臨界風速經測定為16.5 m/s。

應用二維兩自由度耦合顫振分析方法對該平板進行了顫振分析，導數采用了理想平板顫振導數如圖4所示，得到顫振臨界風速16.0m/s，顫振圓頻率為15.6rad/s。

圖3 平板斷面(單位:mm)Fig.3 The model of plate(unit:mm)

圖4 平板的氣動導數Fig.4 Flutter derivatives of the plate

圖5 各項能量的百分比隨風速變化關系Fig.5 The percentage of the energy vs the wind speed

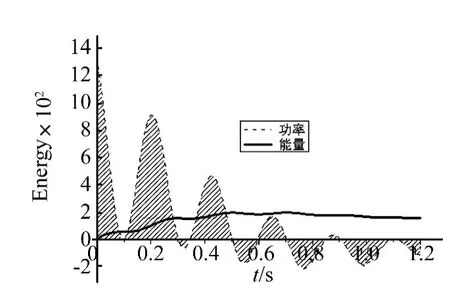
圖6 A項能量的隨時間變化關系(U=16.0 m/s)Fig.6 Aerodynamic energy A vs time(U=16.0 m/s)

圖7 C項能量的隨時間變化關系(U=16.0 m/s)Fig.7 Aerodynamic energy C vs time(U=16.0 m/s)

圖8 C項能量的隨時間變化關系(U=11.9 m/s)Fig.8 Aerodynamic energy C vs time(U=11.9 m/s)

另一方面，隨著時間的推移，A1項消耗的能量越來越多，因此該項能量對系統的穩定性起重要的作用。

圖9 各項能量占總能量的百分比隨風速的變化關系Fig.9 The percentage of the energy vs the wind speed

圖10 A1項能量隨風速的變化關系 (U=16.0 m/s)Fig.10 Aerodynamic energy A1vs time(U=16.0 m/s)

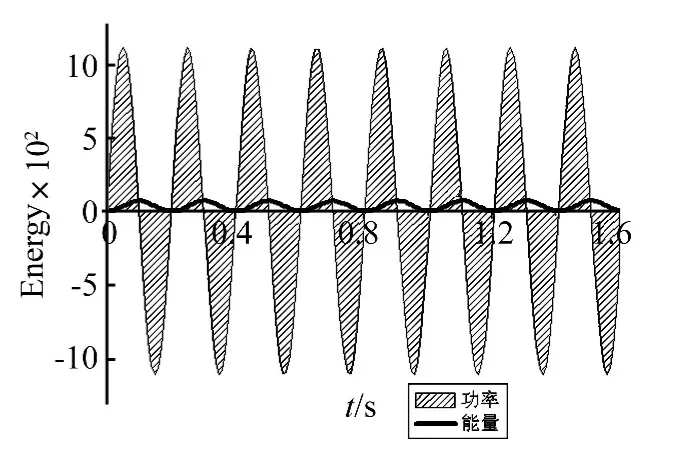
圖11 氣動剛度輸入振動系統能量的隨時間變化關系(U=16.0 m/s)Fig.11 The energy input to the vibration system by aerodynamic stiffness vs time(U=16.0 m/s)

3 結論

本文以二維耦合顫振理論為基礎，應用激勵-反饋的分步分析方法對耦合方程進行解耦，建立了結構-氣流系統顫振能量機理的分析框架，通過引入考慮阻尼影響的初始運動方程詳細推導了扭轉振動和豎向振動系統內部各種作用力輸入到振動系統的能量計算方法，結合平板風洞試驗分析了顫振發生過程中系統內主要作用力的氣動能量輸入特性，從能量轉換的角度對平板彎扭耦合顫振的機理進行了研究，通過上述的研究對平板彎扭耦合顫振的機理可以從以下幾個方面進行闡述:

(2)在平板耦合顫振發生過程中扭轉氣動阻尼力與扭轉振動的速度方向始終是完全的反相位，隨著風速的增加，平板的氣動導數的絕對數值不斷增大，從而使其耗能能力不斷增強，成為扭轉振動的最為主要的耗能因素。

［1］ Matsmnoto M，Yoshizumi F，Yabutani T，et al. Flutter stabilization and heaving-branch flutter.［J］Journal of WEIA，1999，83:289.

［2］ Matsumoto M.Flutter classification of briage girders［M］//Choi，C.K.，Solari，G.，Kanda，J.，eta1.Proceeding of the 1st international symposium on wind and structures for the 21St century.Chcju:Techno-Press，2000:39-79.

［3］Matsumoto M，Shirato H，Shijo R，et al.Flutter stabilization of long span bridges［M］∥ Choi C.K.，Kareem，A.，Matumoto，M.，eta1.Proceeding of the 2nd international symposium on advances in Wind＆structures Busan:Teehno-Press，2002:257-264.

［4］ Yang Y X，Ge Y J，Xiang H F.Coupling effects of degrees of freedom in flutter instability of long span bridges［M］//Choi，C.K.，Kareem，A.，Mastsurnoto，M.，eta1.Proceeding of the 2nd international symposium on advances in wind＆structures Busan:Techn-Press，2002:625-632.

［5］楊詠昕，葛耀君，項海帆.平板斷面彎扭耦合顫振機理研究［J］.工程力學，2006，23(12):2-8.

YANG Yong-xin，GE Yao-jun，XIANG Hai-fan.Research on the coupled bending-torsional flutter mechanism for thin plate sections［J］.Engineering Mechanics，2006，23(12):2-8.

［6］楊詠昕，葛耀君，項海帆.大跨度橋梁中央開槽顫振控制效果和機理研究［J］.土木工程學報，2006，39(7):74-80.

YANG Yong-xin ，GE Yao-jun，XIANG Hai-fan.Flutter control effect and mechanism of central-slotting for long-span bridges.［J］China Civil Engineering Journal，2006，39，(7):74-80.

［7］ Scanlan R H，Tomko J J.Airfoil and bridge flutter derivatives［J］.Journal of Engineering Mechanics Division，1971，97:1717-1737.

［8］劉 高.大跨度懸索橋顫振分析的能量法［J］.中國公路學報，2000，12(3):20-24.

LIU Gao，Flutter analysis of long-span suspension bridges by energy method［J］.China Journal of Highway and Transport，2000，12(3):20-24.

［9］ Scanlan R H.The action of flexible bridges under wind，I:flutter theory［J］.J.Sound and Vib，1978，60(2):187-199.