線性離散時滯系統的輸出反饋鎮定

馬維軍， 朱寰宇， 張顯

(黑龍江大學數學科學學院，黑龍江哈爾濱 150080)

0 引言

由于時變時滯系統較定常時滯系統具有更廣泛的工程背景［1－2］，近幾年得到了人們普遍的關注。特別地，一些學者研究了帶有時變時滯的線性離散系統的穩定性及鎮定問題。然而，穩定性和狀態反饋鎮定問題的研究成果不能直接應用到輸出反饋鎮定問題，因而對輸出反饋鎮定問題的研究就變得尤為重要。Gao等［3］，Liu等［4］，He等［5］，Chen和Fong［6］針對這類系統的輸出反饋鎮定問題進行了研究。

目前對帶有區間時變時滯的離散系統的靜態輸出反饋(static output feedback，SOF)控制器的設計主要采用自由權矩陣和Lyapunov理論相結合的方法。Gao等［3］和Liu等［4］使用相同的Lyapunov函數V(k)來獲得SOF鎮定判據。它們之間的區別是:Gao等［3］忽略了 ΔV(k)中一個負項，而Liu等［4］將這個負項用一個不等式來放縮，這兩種方法增加了結果的保守性。Chen和Fong［6］所選擇的Lyapunov函數雖然表面上不同于文獻［3－4］中的，但是在本質上是相同的。Chen和Fong［6］利用等式來處理前面提到的負項，這降低了結果的保守性。不同于［3－4，6］中的方法，He等［5］構造了包含更多時滯信息的Lyapunov函數，由此得到了具有較低保守性的SOF鎮定判據。為了處理這類系統的SOF鎮定判據中的非線性約束，Gao等［3］，Liu等［4］和He等［5］使用了錐補線性化(cone complementary linearization，CCL)算法，而Chen和Fong［6］利用不等式將非線性約束轉化為線性條件，這當然增加了結果的保守性。進一步，Gao等［3］，Liu等［4］和He等［5］將動態輸出反饋(dynamic output feedback，DOF)鎮定問題轉換成SOF鎮定問題，得到了帶有時變時滯的離散系統的DOF鎮定判據。

本文研究帶有時變時滯的線性離散系統的鎮定問題。通過使用Lyapunov方法且應用Jensen不等式到時滯區間的每個子區間，得到了這類系統的時滯依賴的SOF和DOF鎮定判據。經過理論的和數值的比較發現，本文提出的鎮定判據的保守性弱于文獻中的。由于鎮定判據中存在非線性約束，CCL算法被用來求解輸出反饋增益矩陣。數值算例也說明了本文所給出的方法的優越性。

1 問題描述

考慮如下含區間時變時滯的線性離散系統

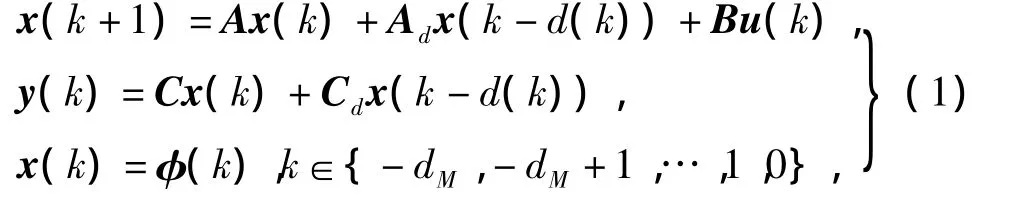
式中:x(k)是n維狀態向量;φ(k)為x(k)的初始狀態;u(k)是m維控制輸入;y(k)是p維可測量輸出;A，Ad，B，C和Cd是具有適當維數的常數矩陣;d(k)為區間時滯并滿足dm≤d(k)≤dM;dm和dM是已知的正整數。

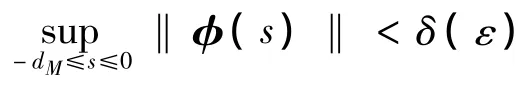
將SOF控制器

代入系統(1)，得到閉環系統

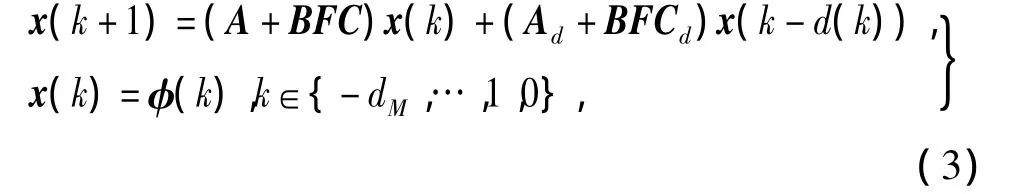
其中，F∈Rm×p是SOF增益矩陣。

將DOF控制器

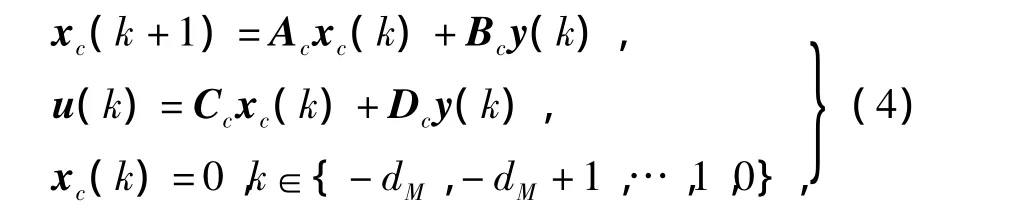
代入系統(1)，得到閉環系統

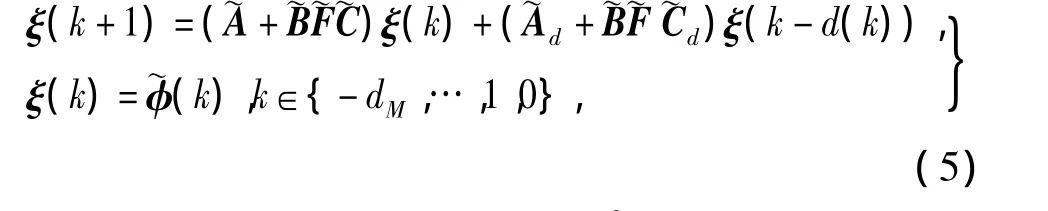
其中，xc(k)是r維控制器狀態，~φ(k)是ξ(k)的初始狀態;

Ac，Bc，Cc和Dc是DOF增益矩陣。

本文的主要目標是:設計形如(2)的SOF控制器和形如(4)的DOF控制器，使得閉環系統(3)和(5)是漸近穩定的，并將本文提出的方法與以往存在的方法進行理論上和數值上的比較。

2 預備知識

引理1［5］Theorem2對于給定的dm和dM，dM＞dm，系統(1)可由控制器(2)鎮定，如果存在實矩陣P＞0，V＞0，Qi＞0(i=1，2，3)，Zj＞0，F，

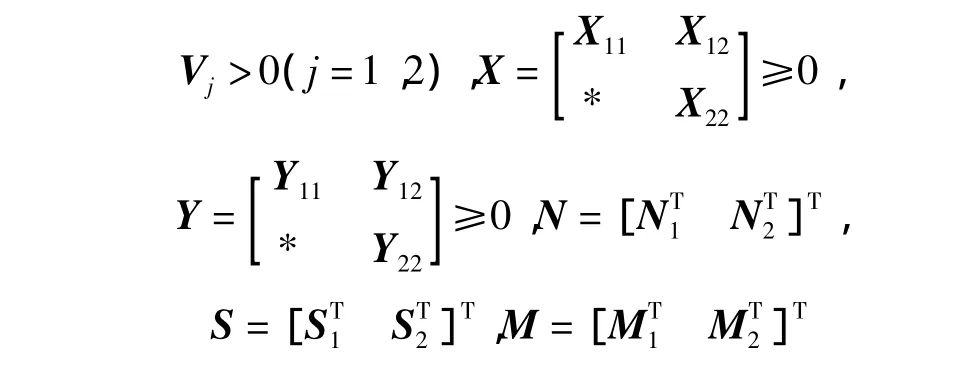
使得

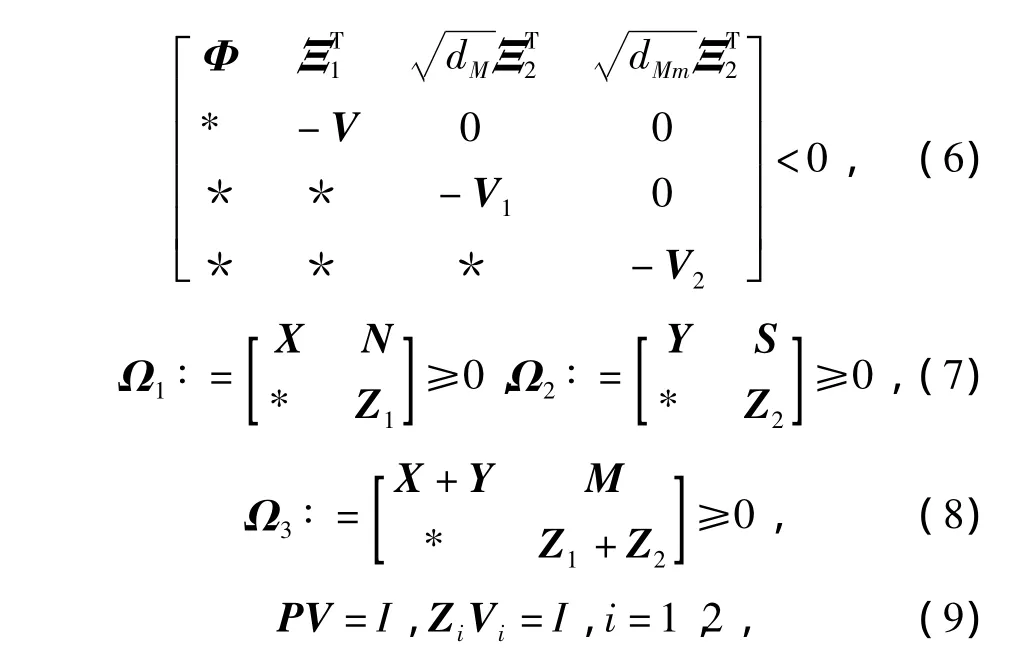
其中

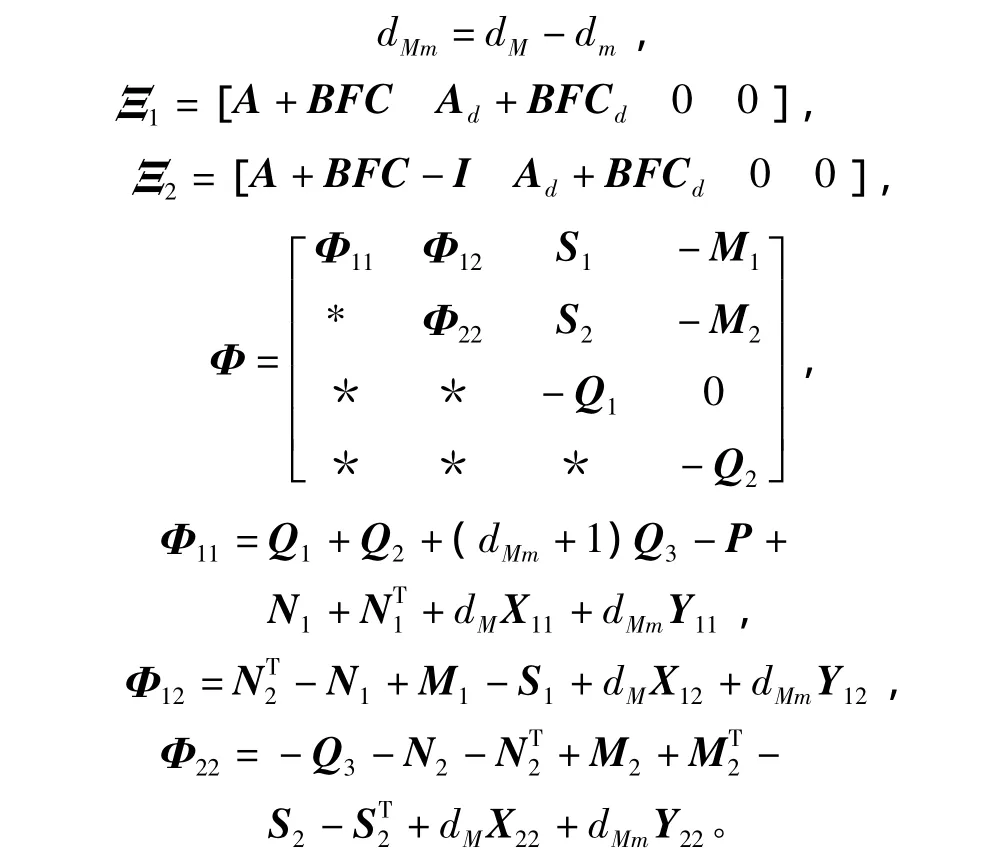
引理2［3］Theorem2對于給定的dm和dM，dM＞dm，系統(1)可由控制器(2)鎮定，如果存在矩陣V＞0，P＞0，V1＞0，G＞0，H，Q＞0，Z＞0和SOF增益矩陣F滿足

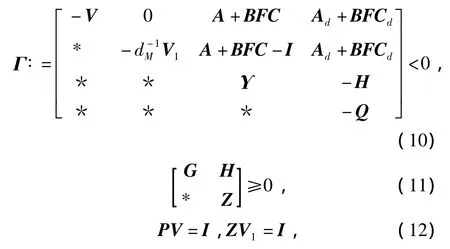
其中，Υ∶=－P+dMG+H+HT+(dMm+1)Q。

引理3［6］Theorem3系統(1)可由控制器(2)鎮定，如果存在矩陣F，L＞0，J＞0，P＞0，Qi＞0，i=2，3，Z＞0，

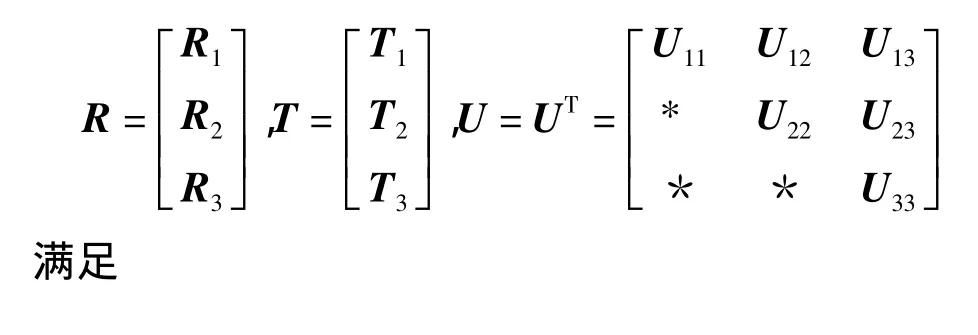
3 靜態輸出反饋鎮定

本節將給出系統(1)可由SOF控制器(2)鎮定的時滯依賴的判據，并將該判據與［5］Theorem 2，［3］Theorem 2和［6］Theorem 3進行理論比較。

3.1 靜態輸出反饋鎮定判據

下面定理給出了系統(1)可由SOF控制器(2)鎮定的充分條件。其主要思想是首先s等分時滯的變化區間，然后分別討論時滯落入每個子區間的情形，從而給出系統(1)可由SOF控制器(2)鎮定的充分條件。通過這個劃分可以降低結果的保守性。

定理1對于給定的正整數s，dm和dM，dM＞dm，系統(1)可由SOF控制器(2)鎮定，如果存在矩陣P＞0，V＞0，Qi＞0(i=1，2，3)，Zj＞0，Vj＞0(j=1，2)和F使得(9)和

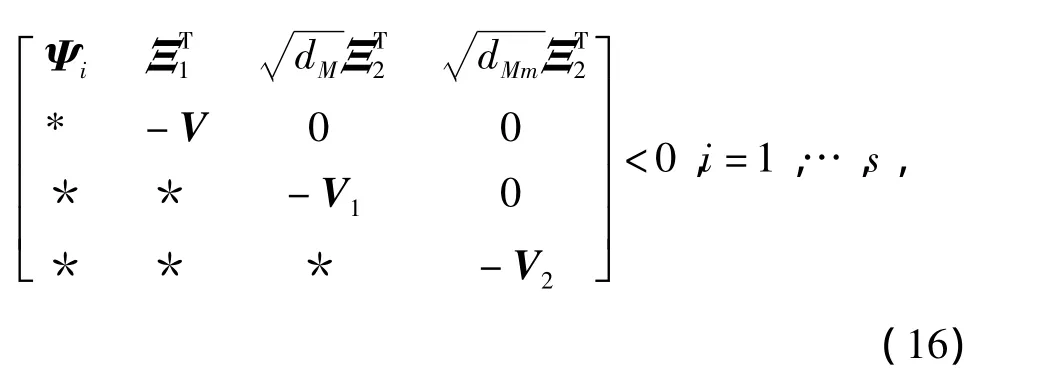
成立，其中dMm，Ξ1和Ξ2同引理1中定義，證

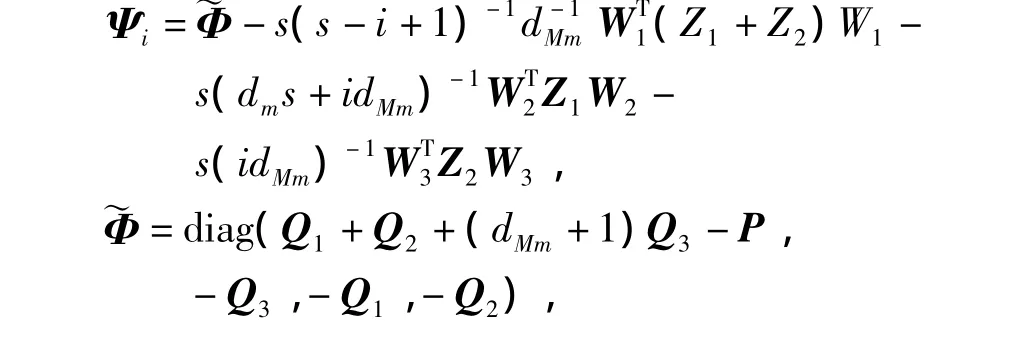
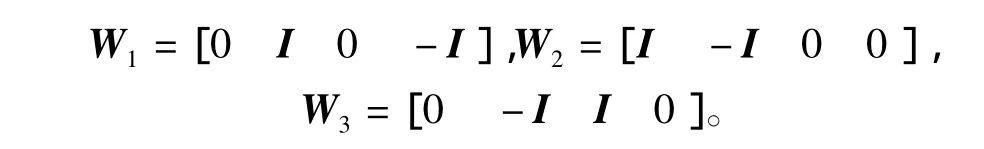
明 設 η(k)=x(k+1)－x(k)，構造Lyapunov函數

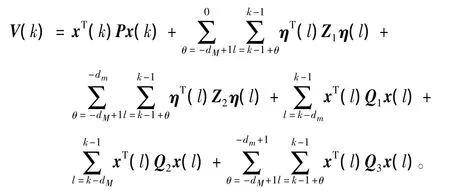
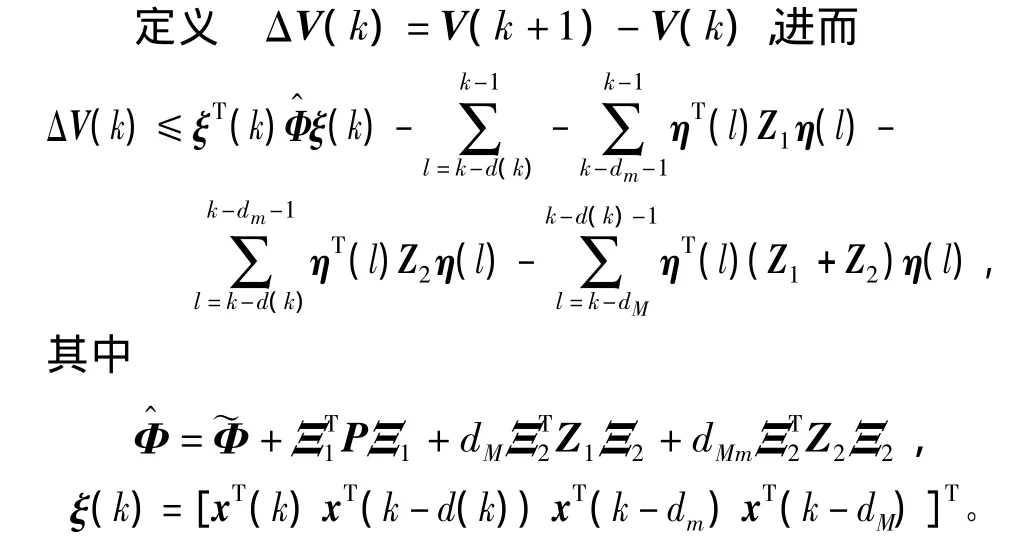
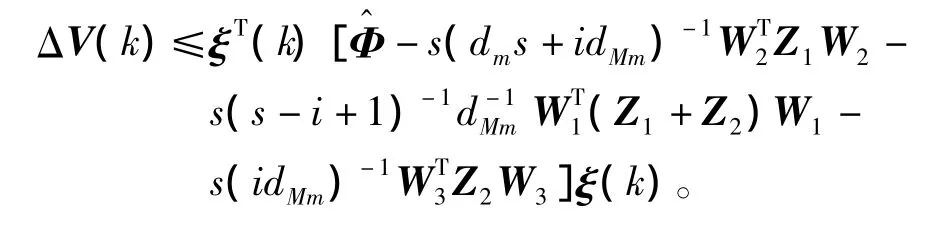
進而利用Schur補引理，式(9)和(16)得ΔV(k)＜0。從而系統(1)可由SOF控制器(2)鎮定。證畢。

3.2 與文獻中已有結論的比較

定理2對于給定的正整數dm和dM，dM＞dm。在約束條件(9)下，如果線性矩陣不等式(6)～(8)成立，那么存在正整數s使得(16)成立。

證明 由式(6)、式(9)和Schur補引理得

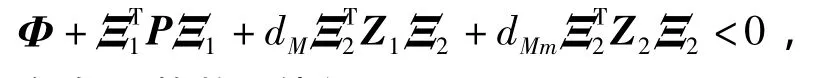
于是存在正整數s使得

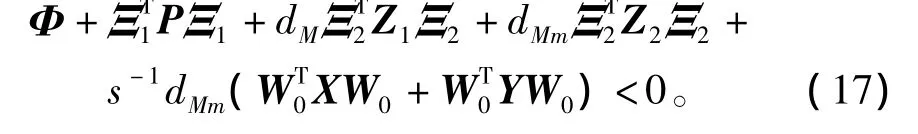
注意到Φ可以寫成

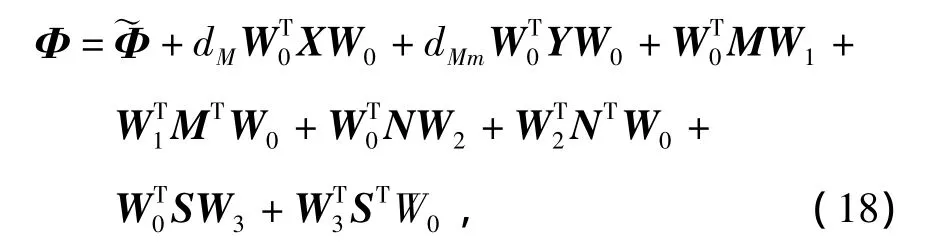
利用Jensen不等式得到

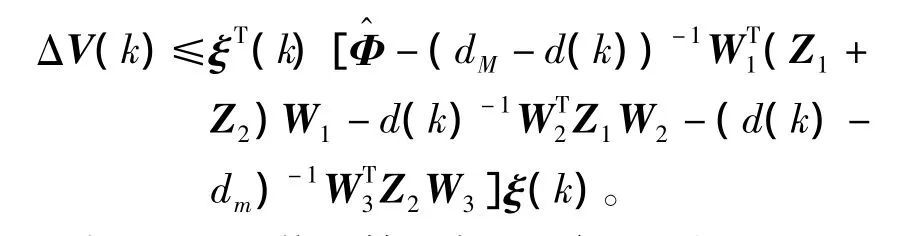
如果d(k)位于第i個子區間，那么

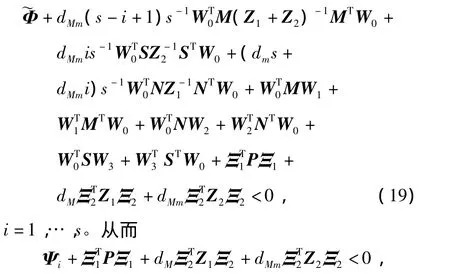
i=1，…，s。再由(9)和Schur補引理知存在正整數s使得(16)成立。證畢。

注記1定理2的證明表明，當正整數s充分大時，定理1的保守性弱于［5］Theorem 2(即引理1)。

定理3對于給定的正整數dm和dM，dM＞dm。如果式(10)、式(11)在約束條件(12)下成立，則當s=1時式(16)在約束條件(9)下成立。

證明 如果式(10)、式(11)在約束條件(12)下成立，則

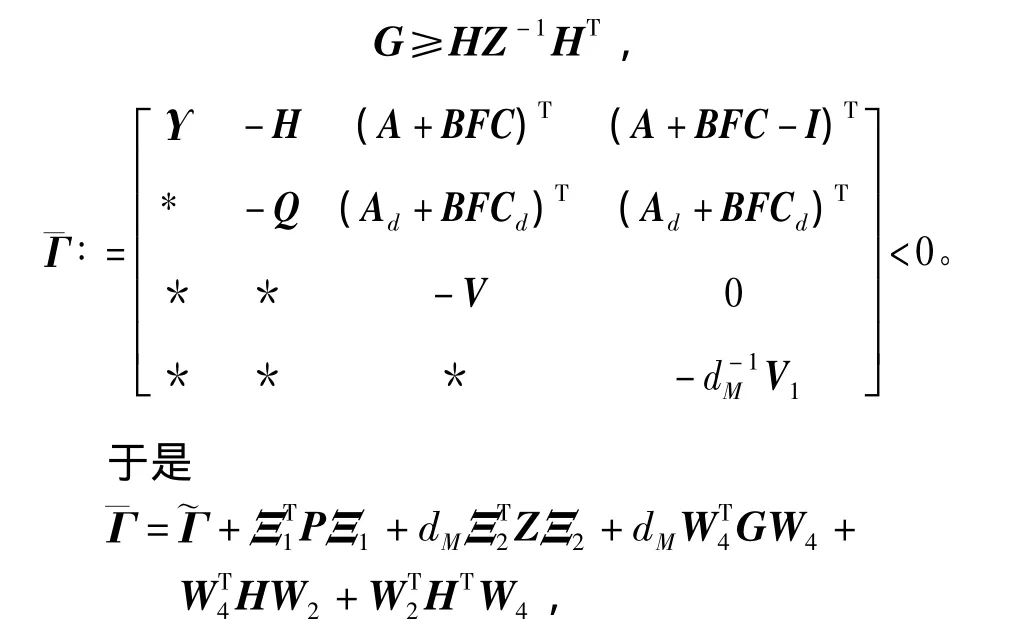
其中W0=I2n[]0，，W1，W2和W3如定理1中定義。再使用式(7)、式(8)得到

其中W4=In[]0，Ξ1，Ξ2和W2如定理1中定義，

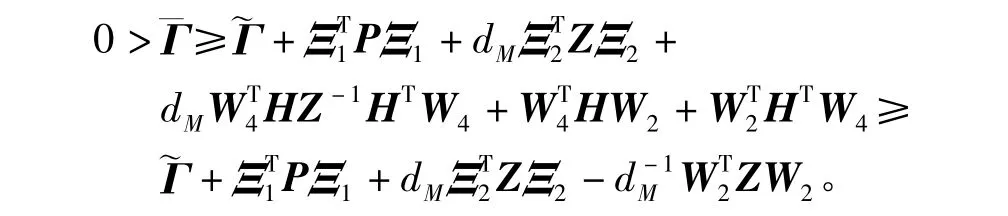
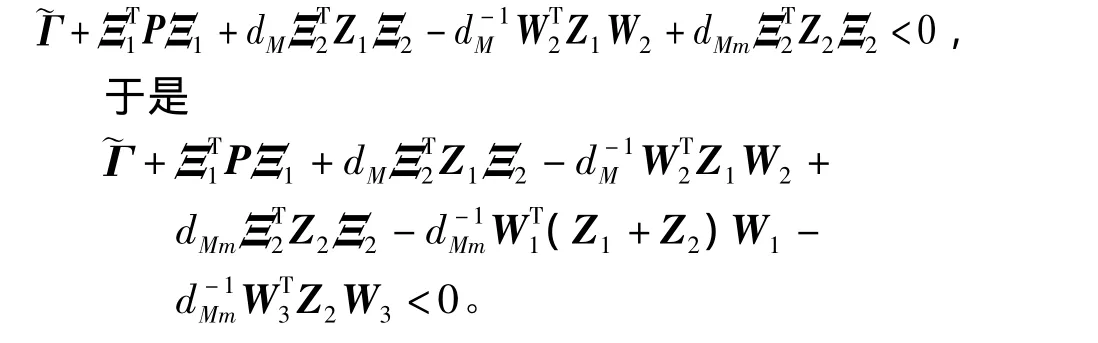
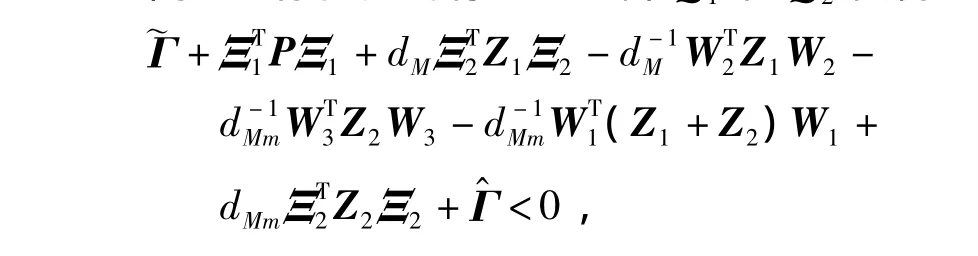
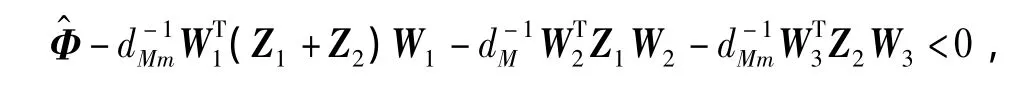
注記2定理3表明，當s=1時定理1的保守性弱于［3］Theorem 2。類似于定理3的證明，可推出定理1的保守性弱于［4］Theorems 6，7。

定理4對給定的正整數dm和dM，dM＞dm。如果式(13)～式(15)成立，那么存在正整數s使得式(16)在約束條件(9)下成立。

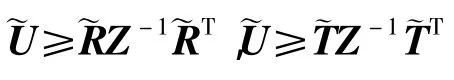
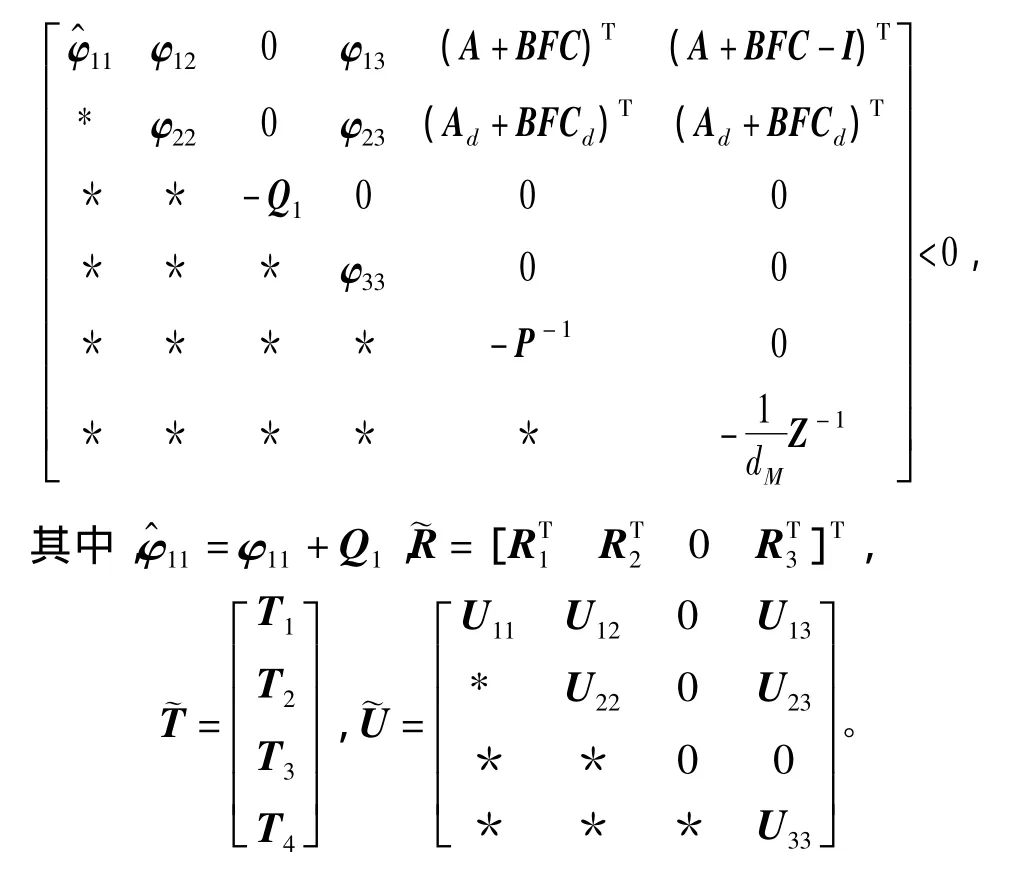
根據Schur補引理可推出

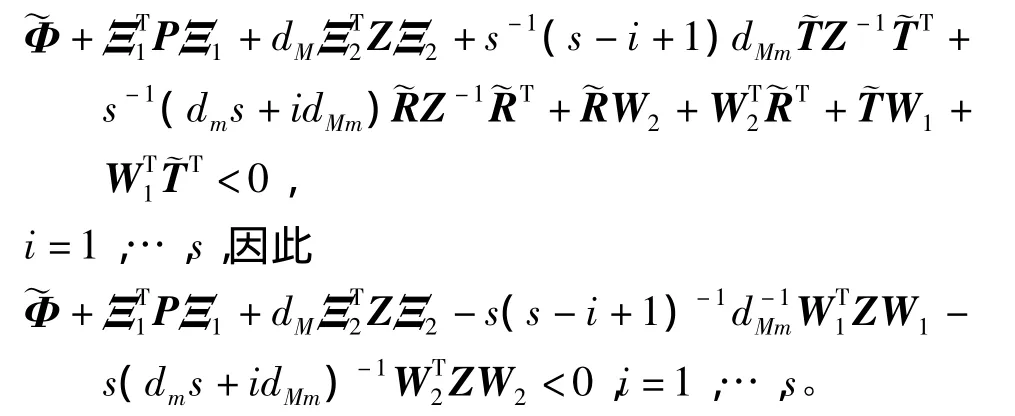
設Z1=Z，那么存在實對稱正定矩陣Z2使得

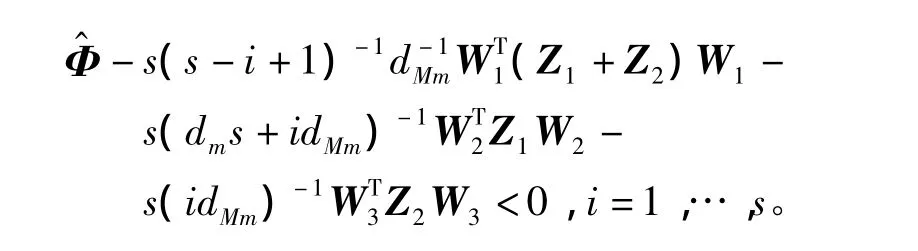
注記3定理4表明定理1的保守性弱于［6］Theorem 3(即引理3)。

4 動態輸出反饋鎮定

類似于定理1的證明，下面的定理給出了系統(1)可通過DOF控制器(4)鎮定的充分條件。

定理5對于給定的正整數s，dm和dM，dM＞dm，系統(1)可由DOF控制器(4)鎮定，如果存在矩陣PT=P＞0，VT=V＞0，=Qi＞0(i=1，2，3)，

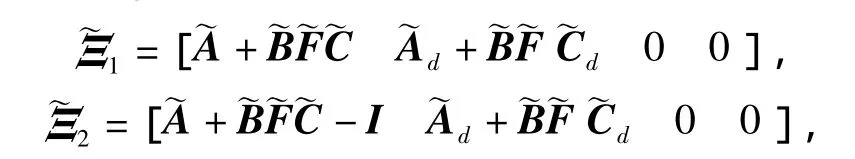
dMm，Ψi，W1，W2，W3同前面定義。

5 數值算例

本節通過兩個例子來說明本文所給出的方法的有效性。為了得到SOF和DOF增益矩陣，下面例子使用類似于文獻［3—5］中的CCL算法在非線性約束(9)下求解式(16)和式(21)。

5.1 SOF鎮定算例1

考慮系統(1)，其中

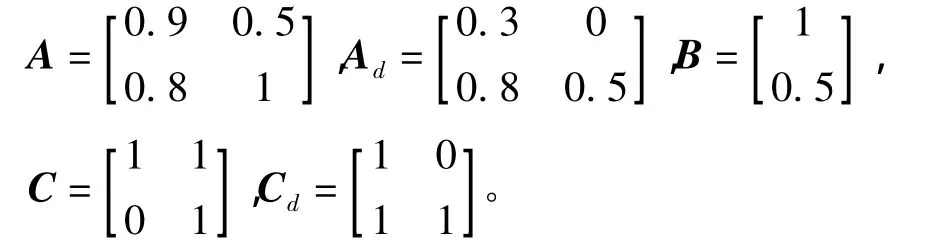
表1給出了由文獻［3－6］中結論與定理1得到的dM的最大值。仿真結果表明定理1比文獻［3－6］中的相應結論有較弱的保守性。另一方面，定理1所要求解的變量個數少于［5］Theorem 2和［6］Theorem 3要求解的，這降低了計算的復雜性。當s=15時，由定理1得到的SOF增益矩陣為F=[－0.349 0－0.193 1]。

表1 當dM=3時，dM的最大值Table 1 Maximums of dMwhen dm=3

5.2 SOF鎮定算例2

考慮系統(1)，其中

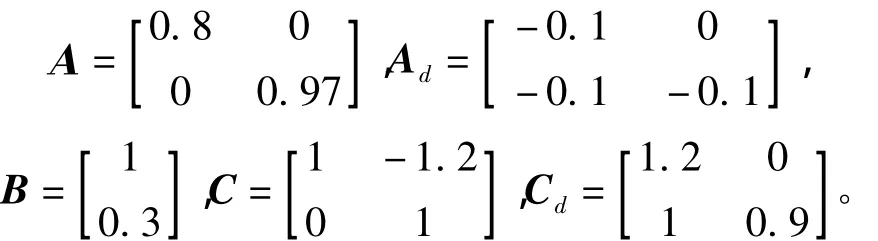
表2給出了由文獻［3－5］與定理5得到的dM的最大值。由此可知，定理5的保守性弱于［3－5］中的相應結論。當s=10，r=2時，由定理5得到的DOF增益矩陣為

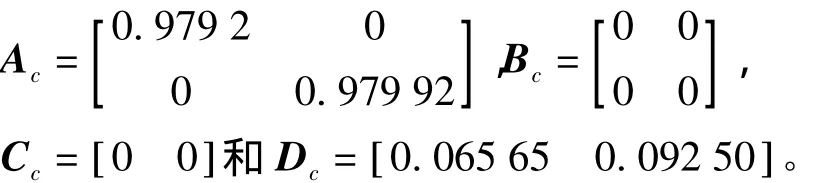
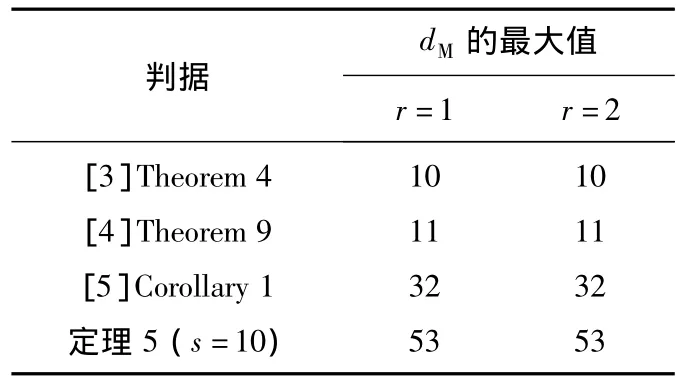
表2 當dm=3時，dM的最大值Table 2 Maximums of dMwhen dm=3

6 結語

本文研究了含區間時變時滯的離散線性系統(1)的SOF和DOF鎮定問題。像引言中提到的，一些學者已經研究了該問題，通過構建Lyapunov函數和利用Jensen不等式技術，本文給出了系統(1)可通過SOF和DOF鎮定的充分條件，并使用CCL算法求解輸出反饋增益矩陣。通過理論的和數值的比較說明了本文所給出的方法的保守性弱于以往學者們所提出的。然而，由于CCL算法有時會失效，還需要進一步尋找求解有非線性約束的線性矩陣不等式的方法。另外，本文的思想和方法可用來解決某些更加復雜系統的鎮定問題，例如具有各種不確定性的離散時滯系統等。

［1］XIONG Junlin，LAM J.Stabilization of linear systems over networks with bounded packet loss［J］.Automatica，2007，43(1):80－87.

［2］GAO Huijun，CHEN Tongwen.Network-based H∞output tracking control［J］.IEEE Transactions on Automatic Control，2008，53(3):655－667.

［3］GAO H，LAM J，WANG C，et al.Delay-dependent output-feedback stabilisation of discrete-time systems with time-varying state delay［J］.IET Control Theory and Applications，2004，151(6):691－698.

［4］LIU X G，MARTIN R R，WU M，et al.Delay-dependent robust stabilisation of discrete-time systems with time-varying delay［J］.IET Control Theory and Applications，2006，153(6):689－702.

［5］HE Yong，WU Min，LIU Guoping，et al.Output feedback stabilization for a discrete-time system with a time-varying delay［J］.IEEE Transactions on Automatic Control，2008，53(10):2372－2377.

［6］CHEN K F，FONG I K.Stability analysis and output-feedback stabilisation of discrete-time systems with an interval time-varying state delay［J］.IET Control Theory and Applications，2010，4(4):563－72.