基于GSM－SVDD的模擬電路故障診斷方法

羅慧， 王友仁

(1.南京農業大學 工學院，江蘇 南京 210031;2.南京航空航天大學 自動化學院，江蘇 南京 210016)

0 引言

由于模擬電路故障的復雜多樣性、廣泛非線性及參數容差等問題，其故障診斷技術至今不成熟。近幾年，人工智能法成為模擬電路故障診斷的研究熱點，其中神經網絡法和支持向量機(support vector machine，SVM)法取得了一定的研究成果［1－4］。與傳統診斷方法相比，人工智能診斷法能有效地解決模擬電路中故障的模糊性、不確定性和非線性等問題。人工智能故障診斷法可視為一種智能故障字典方法，它將各故障狀態下的電路特征作為訓練樣本，采用機器學習方法對其進行訓練，形成包含各類參數的復雜故障字典，診斷時根據故障字典中的參數值，進行故障診斷和定位。

SVDD(support vector domain description)是由Tax等人提出并發展的一種單值分類方法［5－7］，與SVM相比，SVDD是單類分類法，只訓練一類樣本，訓練速度快。與神經網絡相比，SVDD訓練模型中不存在過擬合和求極值點等問題。同時，SVDD對小樣本和非線性問題具有很好的泛化能力，已成功應用在圖像處理［8－9］、人臉識別［10］，故障檢測［11－12］等研究領域。

目前，在模擬電路故障診斷領域，SVDD方法的應用還處于初步研究領域，國內外相關的研究成果均不多。文獻［11］將9種單分類法應用到模擬電路故障診斷中，結果表明SVDD方法的診斷性能優于其它8類方法。文獻［13］將SVDD和D－S(dempster－shafer，D－S)證據理論結合進行模擬電路故障診斷并與SVM相比較，證明該方法的診斷精確度和診斷速度更優。然而，由于元件容差、非線性和有限測試節點等原因，模擬電路中的模糊故障樣本通常位于多個SVDD球體的交叉區域，容易造成誤診，改進SVDD的球體描述邊界是提高SVDD故障診斷性能的有效途徑。

一個好的SVDD球體描述邊界應該是光滑的并盡可能符合數據分布的邊界［14］，為了得到更加柔韌的描述邊界，引入核函數空間映射方法［7］，通常使用高斯核，高斯核的假設前提是數據樣本具有同等性質的輸入特征空間［7］。然而現實中的故障樣本并不完全符合同性且均勻分布的特點，為此，為了能夠得到更好的球體描述邊界，Tax使用核主成分分析(kernel principal component analysis，KPCA)的方法重調核空間中的數據特征，該方法稱為“Kernel Whitening”法［7］。受此啟發，結合譜圖分析理論［15－16］，本文提出一種基于圖譜空間映射原理的“Kernel Whitening”方法來預處理球體描述邊界的特征數據，由特征值對應的Laplace特征向量來描述SVDD球體邊界。

新方法應用到四運放高通濾波電路的故障診斷中，并與標準SVDD和“一對多”SVM診斷方法進行對比，實驗驗證了該方法的可行性和有效性。

1 SVDD基本理論

SVDD是對給定數據集{xi，i=1，2，…，N}通過最小化半徑R2來定義一個體積最小球體，并使盡可能多的xi都包含在該球體內，其二次規劃問題的描述為

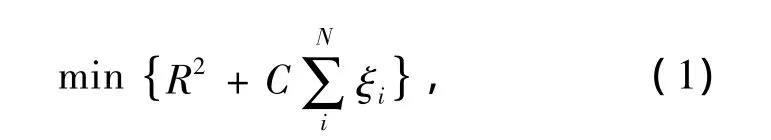
s.t.(xi－a)T(xi－a)≤R2+ξi，?i，ξi≥0。其中:C是懲罰常量;ξi是松弛變量。

用拉格朗日乘子法求解式(1)，轉化為對偶形式的最大化問題，得到

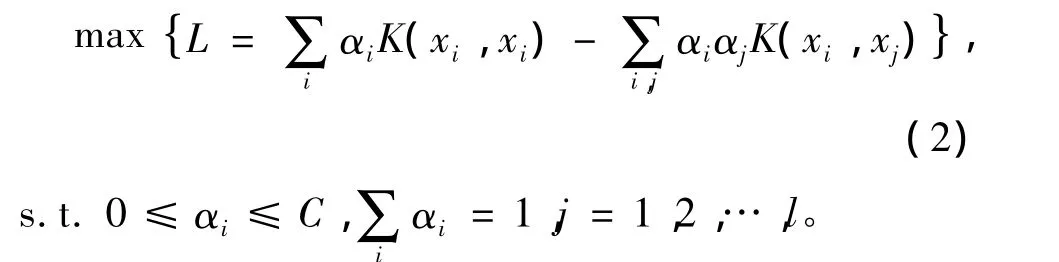
式(2)中，滿足0＜αi≤C條件的樣本稱為支持向量，K(xi，xj)滿足Mercer定理的核函數。

判斷測試點z是否屬于該類球體只需滿足以下條件:

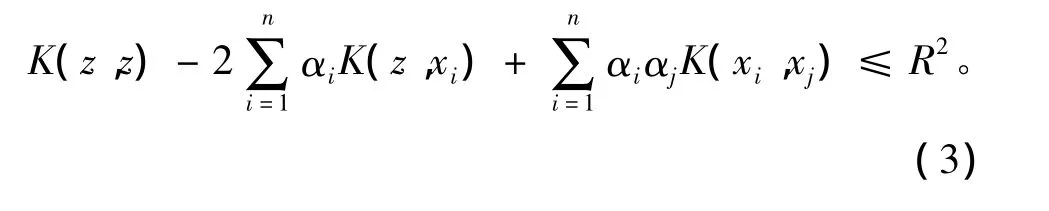
2 圖譜空間映射的SVDD

2.1 圖譜的基本理論

圖譜理論的作用是用圖的譜特征(或譜分解特征)向量來描述圖的結構信息，一旦獲得特征向量，在特征空間中一幅圖就可以被表達為一組數據。譜圖理論分析的基礎是圖的Laplace矩陣，這樣便可將原問題轉換成求解相似矩陣或Laplace矩陣的譜分解［15－16］。

設G是簡單連通圖，D(G)和W(G)分別表示圖G的度對角矩陣和鄰接矩陣，Laplace矩陣分為非規范Laplace矩陣和規范Laplace矩陣。非規范Laplace矩陣表示為L=D－W，規范Laplace矩陣有兩種形式，分別是

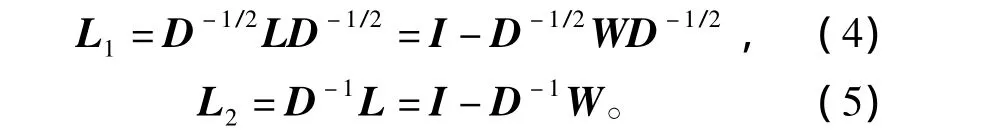
2.2 GSM－SVDD算法描述

為了得到更加柔韌的描述邊界，提高SVDD的診斷性能，在訓練球體時引入核函數將數據樣本映射到高維空間，目的是在高維空間中增加樣本數據的可分性。常用高斯核訓練球體［5－7］，原因是高斯核與數據集在原始空間的位置無關，且不受樣本規范的影響［6］。高斯核的假設前提是輸入樣本集是同性質的(Homogeneous)，即在特征空間中輸入數據在所有方向的距離應該相等［5］。如果特征空間中訓練樣本不同性質并且分布不均勻，SVDD的描述邊界不夠緊湊，會存在大量的空白冗余區，容易造成模糊樣本的誤診。為了改進松弛的描述邊界，本文提出采用圖譜空間映射重調球體描述邊界的特征數據，使規整后的數據具有統一的特征，輸入高斯核的特征樣本具有相同性質，提高SVDD的診斷性能。

給定樣本數量為n、樣本維數為l的樣本集S={s1，s2，…，sn}∈R，GSM－SVDD的算法描述如下:

1)使用高斯函數構造相似矩陣A∈Rn×n，當i=j時，Aii=0，Aij=exp(－ ‖si－sj‖2/2σ2)。

2)構造度矩陣D，度矩陣主對角線上的元素D(i，i)為相似矩陣A的第i行元素之和，其他元素均為0。

3)構造Laplace矩陣，采用公式L=D－1/2AD－1/2。

4)對Laplace矩陣L進行特征值分解，找出前k個最大的特征值所對應的Laplace特征向量M=［m1，m2，…，mk］∈Rn×k。

5)用k個Laplace特征向量代表原始訓練樣本，并對其進行歸一化處理。

6)采用拉格朗日乘子法求解式(2)，再次通過高斯核映射得到SVDD的球體描述邊界，計算得到球體的球心位置和半徑。

GSM－SVDD分類方法中有3個未知參數:

1)高斯核參數，分別是第一次Laplace譜映射空間的高斯核參數σ1和第二次訓練球體時核空間映射的高斯核參數σ2。核參數σ1影響特征數據樣本在空間的分布結構，核參數σ2影響球體的描述邊界。

2)懲罰參數C，控制樣本錯分率和球體體積之間的折中，主要影響球體半徑的大小和支持向量的個數。

3)Laplace譜空間中特征樣本維數k，理論上會存在k個理想的彼此分離簇的有限數據集，它們將彼此正交的分布于k維空間中的單位球上［17］。

3 基于GSM－SVDD的模擬電路診斷

基于GSM－SVDD的模擬電路智能故障診斷方法是一種離線診斷方法，其故障診斷流程如圖1所示，該方法的具體實現步驟如下:

1)對待測電路施加測試激勵，采集測試節點處的節點電壓值作為故障樣本。

2)將故障樣本分為訓練樣本和測試樣本。

3)根據GSM－SVDD描述算法對每類訓練樣本訓練診斷球體，訓練得到GSM－SVDD描述球體的個數等于訓練樣本的故障類數，得到各個球體的球體半徑和球心位置。

4)計算測試樣本到各類球體球心之間的距離判斷測試樣本的故障類別。采用基于距離測度的最小相對距離法則實現GSM－SVDD法的多類診斷，其判斷函數是

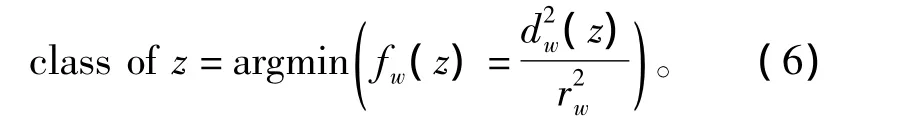
其中:dw(w=1，2，…，n，n是故障類數)是測試樣本z到球體w的距離;rw是球體w的半徑。

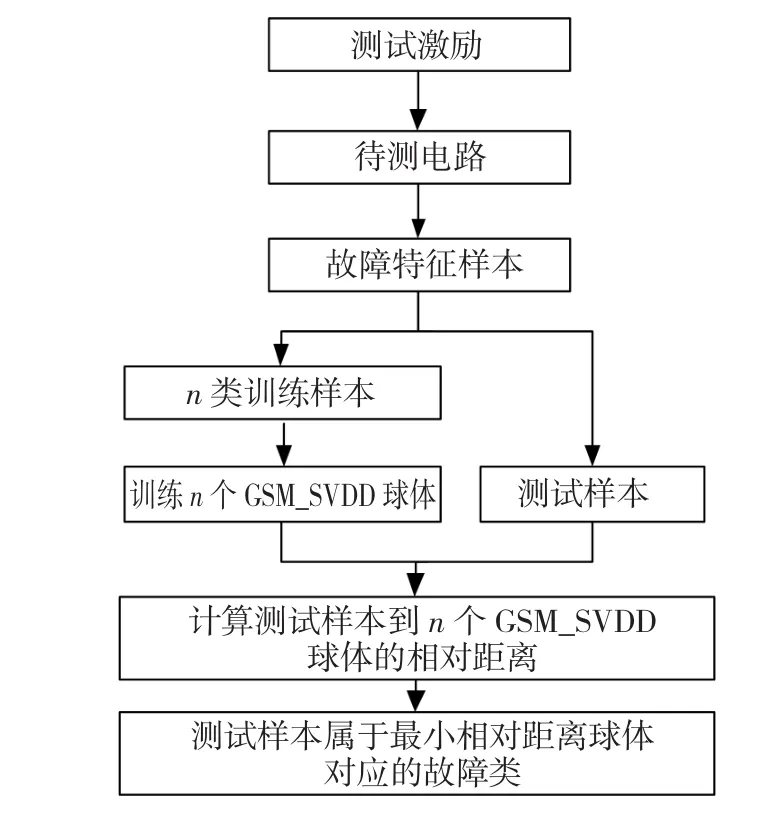
圖1 基于GSM－SVDD的故障診斷流程圖Fig.1 Fault diagnosis flow chart based on GSM－SVDD

4 實驗結果分析

4.1 Laplace譜映射的樣本特征

首先，將Laplace譜映射特征和核PCA映射特征進行對比。實驗中任意選擇三類特征樣本作為比較，原始空間的特征樣本為二維特征。圖2(a)是特征樣本的原始空間分布，圖2(b)和圖2(c)分別是核PCA映射特征和Laplace譜映射特征的空間分布，三類樣本均采取了歸一化處理。

由圖2可知，經過特征空間的一次映射后，核PCA法和Laplace譜法映射后的樣本在特征空間的分布均發生了明顯改變。在Laplace譜特征空間中，映射后特征樣本的分布近似圍成半個橢圓，由于使用高斯函數構造相似矩陣，可計算得到exp(－‖sisi‖2/2σ2)=1，Aij=1，A=D=E，即經Laplace譜空間映射后所有樣本的特征向量的模值均為1。因此，可以看出Laplace譜映射能明顯改變原始特征樣本的空間分布，且改變后特征樣本的模值均相等，更適合高斯核的SVDD球體訓練中要求數據樣本具有同等性質的假設前提。

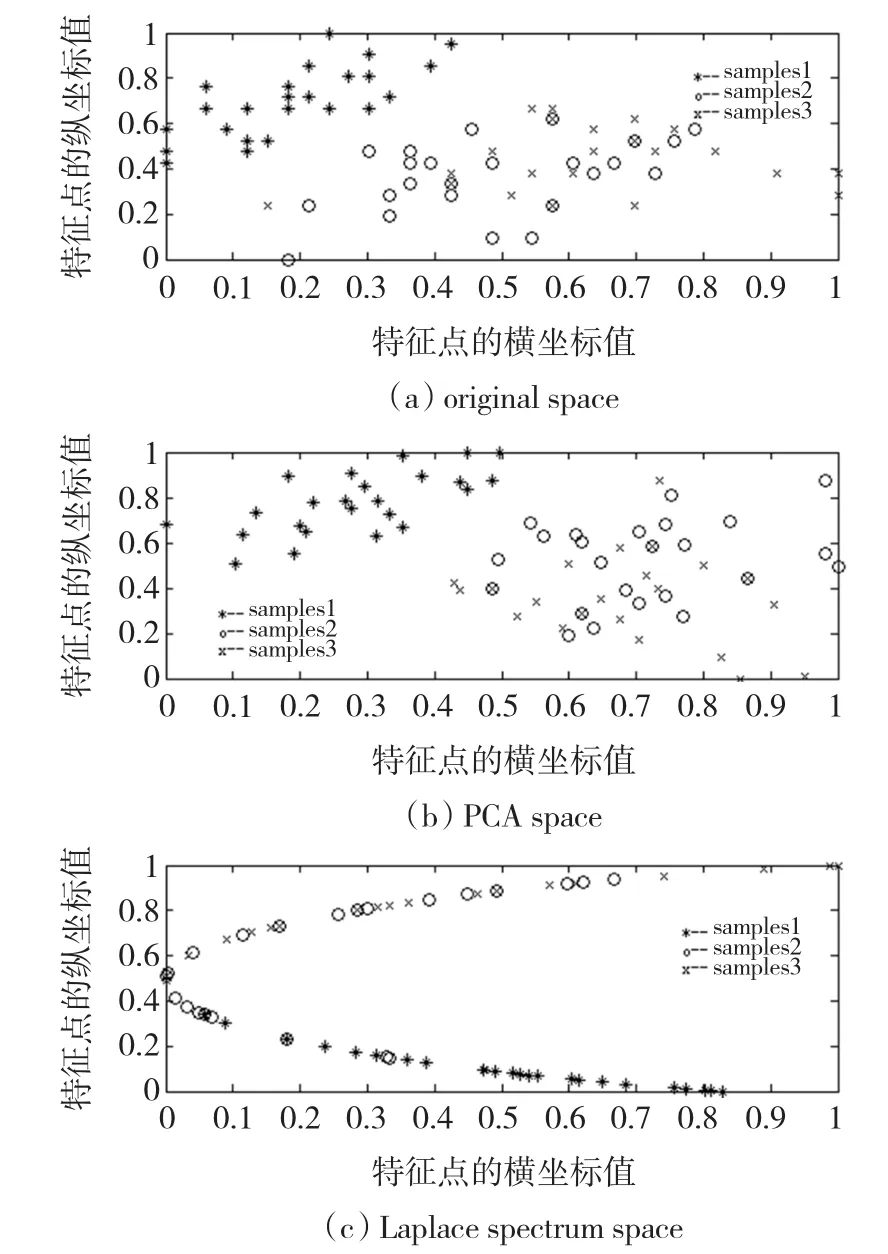
圖2 樣本的特征分布Fig.2 Feature distribution of samples

4.2 四運放高通濾波電路的故障診斷

采用四運放高通濾波電路［2］作為測試診斷對象。元器件正常參數及電路拓撲結構見圖3，輸入節點Vi端的激勵信號是一個幅度為5 V，脈寬為10 μs的脈沖電壓［2］。采用Pspice軟件仿真待測電路，其中電容容差設置為10%，電阻容差為5%，即認為電容值在其標稱值±10%內以及電阻值在其標稱值±5%范圍內波動，采集Out輸出節點的電壓值作為故障樣本，50次蒙特卡洛分析。本文方法是離線診斷測試，其目的是驗證新方法的有效性，共設置12類故障見表1，其中“↑”表示故障值增大，“↓”表示故障值減小，加上電路正常狀態，13類故障模式共采集650個特征樣本，其中，訓練樣本260個，測試樣本390個。用13類故障模式的訓練樣本訓練得到13個GSM－SVDD球體用于診斷測試樣本。

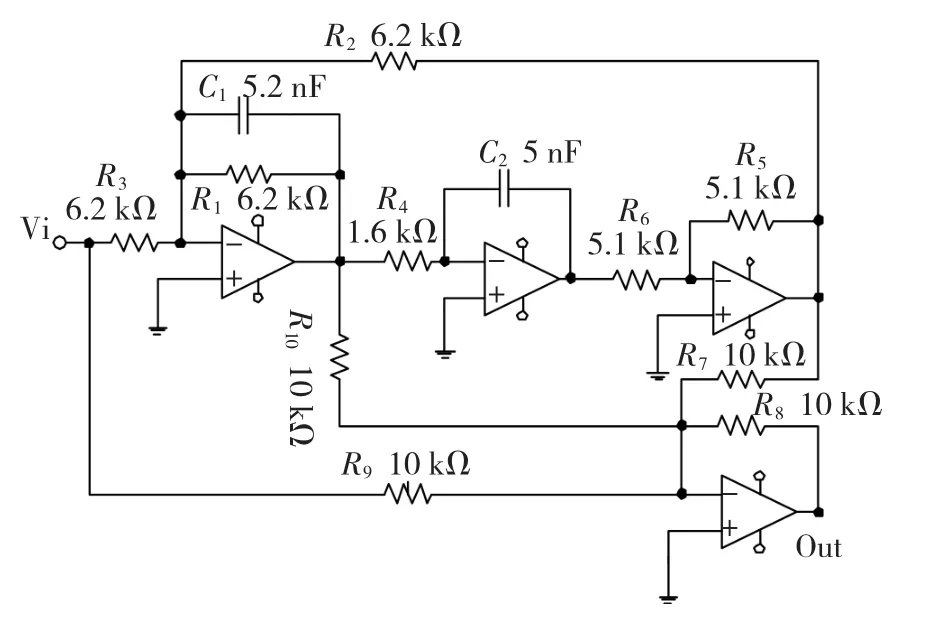
圖3 四運放高通濾波電路Fig.3 Four opamp biquad high-pass circuit

表1 四運放高通濾波電路的故障設置Table 1 Fault models of four opamp biquad high-pass circuit

實驗中采用交叉驗證方法來選擇核參數σ1、σ2、懲罰參數C和Laplace譜空間中的特征樣本維數k。首先確定特征樣本的維數k，實驗中設置k的變化范圍是［2，20］。由19種不同維數的特征樣本訓練的診斷球體的結果如圖4所示，當k=5時，GSM－SVDD診斷球體能獲得最優的診斷準確率。采用相同的方法選擇其他參數，令σ1=σ2變化范圍從7到10且步長為0.1，懲罰參數C從1到10且步長為1，最終確定 σ1=σ2=8.3，C=6。

用最優的參數訓練得到13個GSM－SVDD診斷球體，并采用最小相對距離法則診斷測試樣本，本文方法與標準SVDD和“一對多”SVM診斷方法進行對比，診斷結果如表2所示。

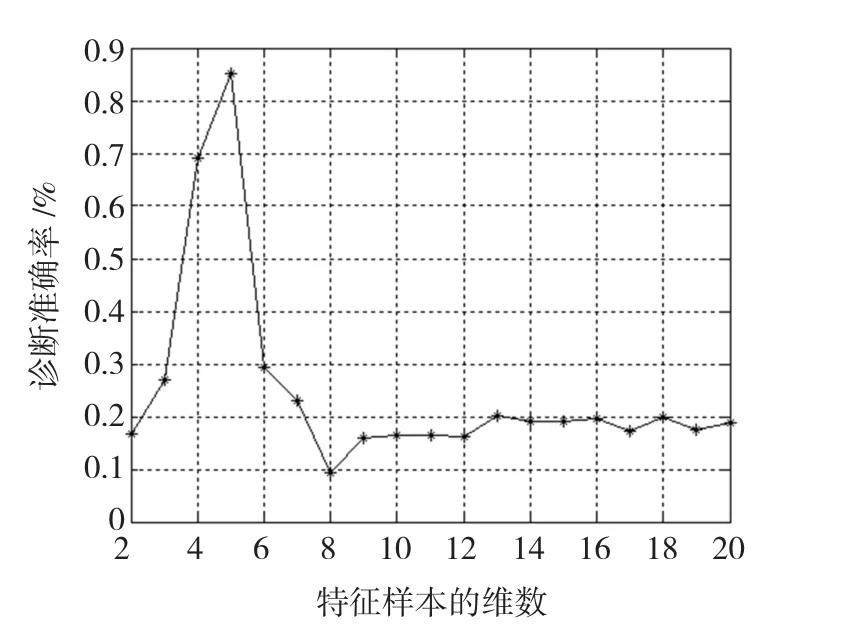
圖4 Laplace譜空間中不同維數特征樣本的診斷曲線Fig.4 Diagnostic curve with different dimension samples in Laplace spectrum space

表2 不同方法的診斷結果Table 2 Diagnostic results with different classifiers(%)

由表2可知，GSM－SVDD方法的平均診斷結果為91.54%，標準SVDD和SVM診斷方法的平均診斷結果分別為89.74%和84.38%，本文方法的平均診斷結果優于標準SVDD和SVM診斷方法。尤其對故障類f12，采用標準SVDD和SVM方法時，故障類f12診斷準確率分別只有10%和3.3%，說明該類故障為典型的模糊故障，模糊故障會陷入標準SVDD多個球體的交叉區域以及SVM分類面的交叉區域，因此很難正確判斷。本文方法通過Laplace譜映射改變了原始特征樣本的空間分布，增強了在原始空間中不可分故障樣本在譜空間中的可區分性，模糊故障類f12在Laplace譜空間中的可診性明顯增強，診斷準確率提高到63.33%。

5 結語

本文研究了一種新的模擬電路智能故障診斷方法，針對SVDD診斷法在模擬電路中容易造成模糊故障樣本誤診的不足，提出了一種基于GSM－SVDD的模擬電路故障診斷方法。對四運放高通濾波電路進行測試診斷，并與標準SVDD和“一對多”SVM診斷方法進行對比，實驗表明通過Laplace譜映射改變原始特征樣本的空間分布，可增強故障樣本的可診性，新方法提高了模擬電路故障診斷的平均準確率，實驗結果驗證了GSM－SVDD方法的有效性。

另外，實驗中新方法僅對模擬電路的單故障進行了測試診斷，當電路系統中兩個及兩個以上的元件發生故障時，在獲得故障樣本的前提下，該方法只能將多個元件發生故障當成是一類“特殊的單類故障”進行診斷，無法做到多個故障元件的定位。如何將智能故障診斷方法和傳統的參數辨識或故障驗證方法結合起來進行模擬電路多故障的診斷和定位有待于進一步的研究。

［1］ALLIPI C，CATELANI M，FORT A，et al.SBT soft fault diagnosis in analog electronic circuits:a sensitivity-based approach by randomized algorithms［J］.IEEE Transactions on Instrumentation and Measurement，2002，51(5):1116－1125.

［2］AMINIAN F，AMINIAN M，COLLINS H W.Analog fault diagnosis of actual circuits using neural networks［J］.IEEE Transactions on Instrumentation and Measurement，2002，51(3):544－549.

［3］CATELANI M，FORT A.Fault diagnosis of electronic analog circuits using a radial basis function network classifier［J］.Measurement，2000，28(3):147－158.

［4］羅慧，王友仁，崔江，等.電力電子電路多源特征層融合故障診斷方法［J］.電機與控制學報，2010，14(4):92－96.

LUO Hui，WANG Youren，CUI Jiang，et al.Intelligent fault diagnosis for power electronic circuits based on multi-source featurelevel fusion［J］.Electric Machines and Control，2010，14(4):92－96.

［5］TAX D M J，DUIN R P W.Support vector domain description［J］.Pattern Recognition Letter，1999，20(1):1191－1199.

［6］TAX D M J，DUIN R P W.Support vector data description［J］.Machine Learning，2004，54(1):45－66.

［7］TAX D M J，JUSZCZAK P.Kernel whitening for one-class classification［J］.International Journal of Pattern Recognition and Artificial Intelligence，2003，17(3):333－347.

［8］SJOSTRAND K，HANSEN M S，LARSSON H B，et al.A path algorithm for the support vector domain description and its application to medical imaging［J］.Medical Image Analysis，2007，11(5):417－428.

［9］JORDI M M，LORENZO B，VALLS C G.A support vector domain description approach to supervised classification of remote sensing images［J］.IEEE Transactions on Geoscience and Remote Sensing，2007，45(8):2683－2692.

［10］LEE S W，PARK J，LEE S W.Low resolution face recognition based on support vector data description［J］.Pattern Recognition，2006，39(9):1809－1812.

［11］ZHANG Y，WEI X Y，JIANG H F.One-class classifier based on SBT for analog circuit fault diagnosis［J］.Measurement，2008，41(4):371－380.

［12］BU H G，WANG J，HUANG X B.Fabric defect detection based on multiple fractal features and support vector data description［J］.Engineering Applications of Artificial Intelligence，2009，22(2):224－235.

［13］唐靜遠，師奕兵，姜丁，等.基于SVDD和D－S理論的模擬電路故障診斷［J］.測控技術，2008，27(9):65－68.

TANG Jingyuan，SHI Yibing，JIANG Ding，et al.Analog circuit fault diagnosis based on SVDD and dempster-shafer theory［J］.Measurement and Control Techniques，2008，27(9):65－68.

［14］GUO S M，CHEN L C，TSAI J S H.A boundary method for outlier detection based on support vector domain description［J］.Pattern Recognition，2009，42(1):77－83.

［15］MIROSLAV F.Algebraic connectivity of graphs［J］.Czechoslo-vak Mathematical Journal，1973，23(98):298－305.

［16］ANDREW Y N，JORDAN M I，YAIR W.On spectral clustering:analysis and an algorithm［J］.Neural Information Processing Systems，2001，14:849－856.

［17］王玲，薄列峰，焦李成.密度敏感的半監督譜聚類［J］.軟件學報，2007，18(10):2412－2422.

WANG Ling，BO Liefeng，JIAO Licheng.Density-sensitive semi-supervised spectral clustering［J］.Journal of Software，2007，18(10):2412－2422.

［18］蔡曉妍，戴冠中，楊黎斌.譜聚類算法綜述［J］.計算機科學，2008，35(7):14－18.

CAI Xiaoyan，DAI Guanzhong，YANG Libin.Survey on spectral clustering algorithm［J］.Computer Science，2008，35(7):14－18.