應用層次分析法確定社區-居家式老年人長期照護評價指標權重

王玉環 黃方超 (石河子大學醫學院醫學人文研究所，新疆 石河子 832002)

在多指標綜合評價中，權重的合理確定對構建綜合評價模型至關重要。權重系數直接影響到綜合評價的結果。被評價對象的優劣、次序可隨權重的變化而發生變化，反過來，科學的定權還可以彌補指標選取的不足〔1〕。本研究前期階段運用Delphi法構建社區-居家式老年人長期照護評價指標體系的具體方案〔2〕，本文將重點報告如何確定該評價指標體系的權重和最終確定的權重分布。

1 資料與方法

1.1 評價指標體系確立 課題組自行編制了社區-居家式老年人長期照護評價指標體系的專家咨詢問卷，運用Delphi法進行了2輪專家咨詢，專家意見得到一致，形成了包括7項一級指標(服務內容、從業人員資格準入、服務對象界定分級、長期照護服務機構、長期照護效果評價、財政支持、運行與監管)、27項二級指標、16項三級指標構成的社區-居家式老年人長期照護評價指標體系。

1.2 層次分析法確定指標權重 層次分析法〔3，4〕(AHP)是美國科學家、匹茲堡大學的Thomas等于20世紀70年代提出的一種定性和定量分析相結合的系統化、層次化的分析方法。本研究運用AHP法確立社區-居家式老年人長期照護評價指標體系的權重，具體步驟如下:

1.2.1 構建遞階層次結構模型 根據AHP理論構建目標層、準則層、指標層、方案層等遞階層次結構模型，如圖1所示。

1.2.2 建立兩兩比較判斷矩陣 經過前期的Delphi法專家咨詢，已知各級評價指標的重要性賦值均數。重要性賦值均數的高低表明了各指標的重要性的差異。可以先計算評價指標關于某個評價目標的重要程度均值之差，查找均值之差所對應的Saaty相對重要性等級，轉化為Saaty相對重要性等級后再進行兩兩對比。假設Zij和Zik為某一評價方面中任意兩個指標的重要性分值，為了構造判斷矩陣A，規定如下:

若0.25＜Zij-Zik≤0.5，Zij比 Zik稍微重要，Saaty標度取3;

若0.75＜Zij-Zik≤1.0，Zij比 Zik相當重要，Saaty標度取5;

若1.25＜Zij-Zik≤1.5，Zij比 Zik強烈重要，Saaty標度取7;

若1.75＜Zij-Zik，Zij比Zik極端重要，Saaty標度取9;

如差值在兩個尺度之間，則Saaty標度為2，4，6，8。

據此原則，可構造出判斷矩陣。

1.2.3 判斷矩陣的一致性檢驗 判斷矩陣的一致性檢驗〔5〕可通過計算一致性比率C.R(consistency ratio)來實現。C.R是一致性指標C.I與同階的平均隨機一致性指標R.I的比值。公式:C.R=C.I/R.I。用一致性比率C.R來檢驗判斷矩陣的一致性。C.R越小，判斷矩陣的一致性越好。一般認為，當C.R≤0.1時，判斷矩陣符合滿意的一致性標準，層次單排序的結果是可以接受的;否則，需要修正判斷矩陣，直至檢驗通過。

①一致性指標C.I(consistency index)。C.I=(λmax-m)/(m-1)，式中，m為判斷矩陣的階數，λmax為判斷矩陣的最大特征值。②平均隨機一致性指標(random index)，記作R.I;R.I指標隨判斷矩陣的階數而變化，階數 1、2、3、4、5、6、7、8、9 的 RI分別為 0、0、0.52、0.89、1.12、1.26、1.36、1.41 和 1.46。這些值是用隨機方法構造判斷矩陣，經過500次以上的重復計算，求出一致性指標，并加以平均而得到的。

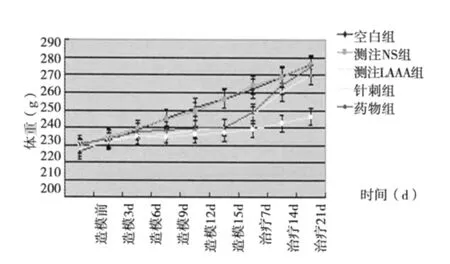
圖1 社區-居家式老年人長期照護評價指標體系層次模型

2 結果

2.1 準則層(一級指標)權重 設定 B1、B2、B3、B4、B5、B6、B7分別代表服務內容、從業人員資格準入、服務對象界定分級、長期照護服務機構、長期照護效果評價、財政支持、運行與監管七個一級指標，Delphi專家咨詢結果顯示其重要性賦值均數分別為 4.89、4.67、4.22、4.67、4.78、4.89、4.78，即 B1=4.89，B2=4.67、B3=4.22、B4=4.67、B5=4.78、B6=4.89、B7=4.78，根據Saaty標度確定方法，可構造兩兩比較判斷矩陣A-B，見表1。根據既定規則，經轉化，形成判斷矩陣，見表2。

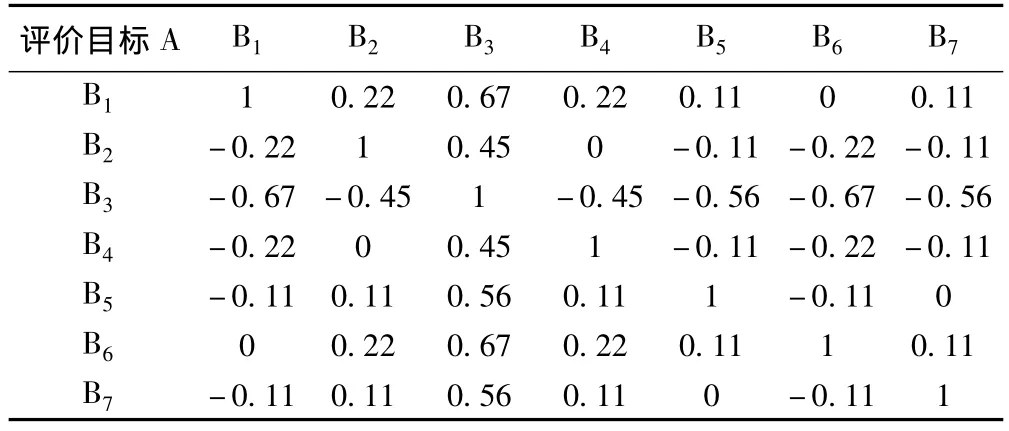
表1 未經轉化的A-B判斷矩陣

表2 A-B判斷矩陣及權重計算

經計算，可得B1～B7的相應權重(如矩陣中所示)，λmax=7.009 8，m=7，則 C.I=0.001 4;查表可知，m=7 時，R.I=1.36;則C.R=0.001 2。C.R≤0.1，判斷矩陣符合滿意的一致性標準。因此，相對于社區-居家式老年人長期照護評價這一總目標，服務內容、從業人員資格準入、服務對象界定分級、長期照護服務機構、長期照護效果評價、財政支持、運行與監管在整個評價指標中的權重系數分別為0.171 0，0.132 2，0.088 6，0.132 2，0.152 5，0.171 0，0.152 5。

2.2 指標層(二級指標和三級指標)權重 依照上述步驟構建判斷矩陣 B1-C、B2-C、B3-C、B4-C、B5-C、B6-C、B7-C、，計算各二級指標權重并進行一致性檢驗，見表3～表9;三級指標權重同法求得。然后進一步計算各層次指標對總目標層的權重，并依次按照各級指標權重大小排序，見表10。

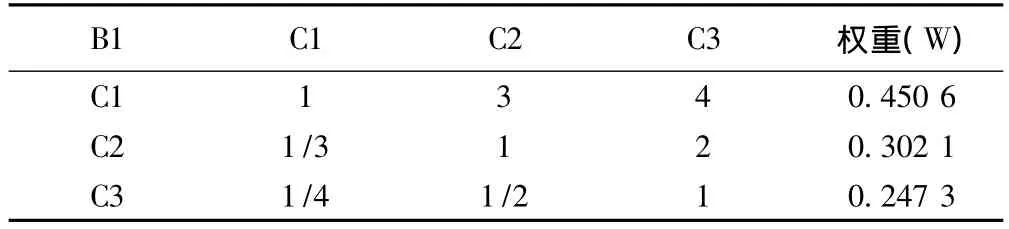
表3 B1-C判斷矩陣及權重計算

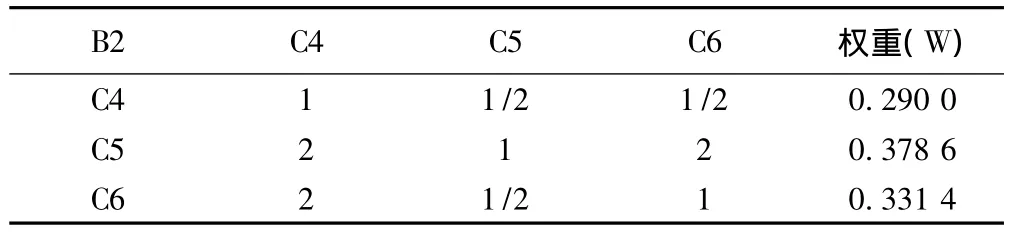
表4 B2-C判斷矩陣及權重計算

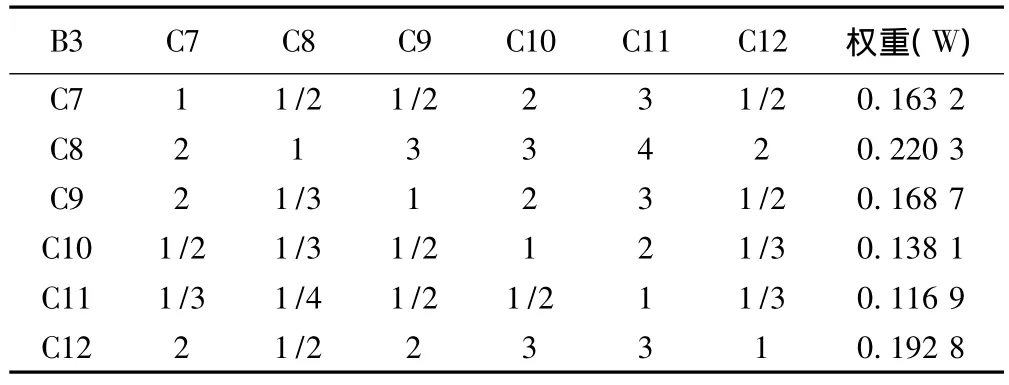
表5 B3-C判斷矩陣及權重計算

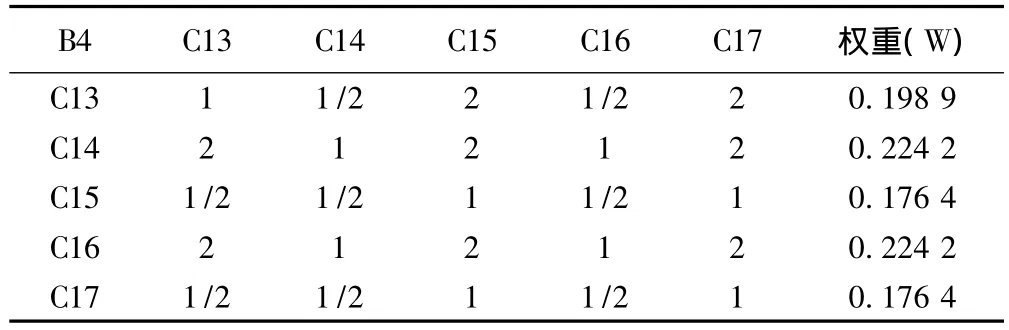
表6 B4-C判斷矩陣及權重計算

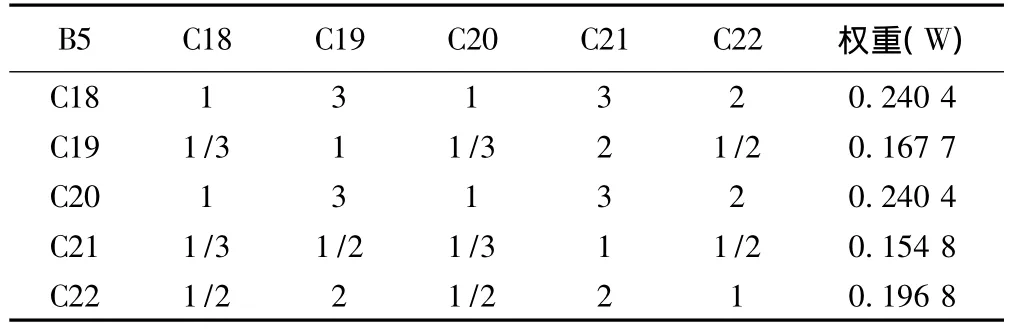
表7 B5-C判斷矩陣及權重計算

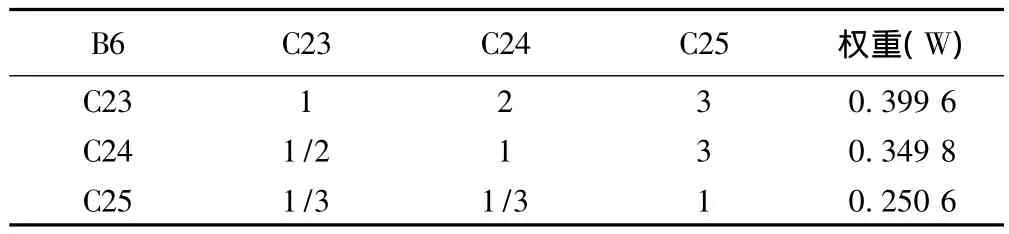
表8 B6-C判斷矩陣及權重計算

表9 B7-C判斷矩陣及權重計算

2.3 社區-居家式老年人長期照護評價指標體系及其權重見表10。

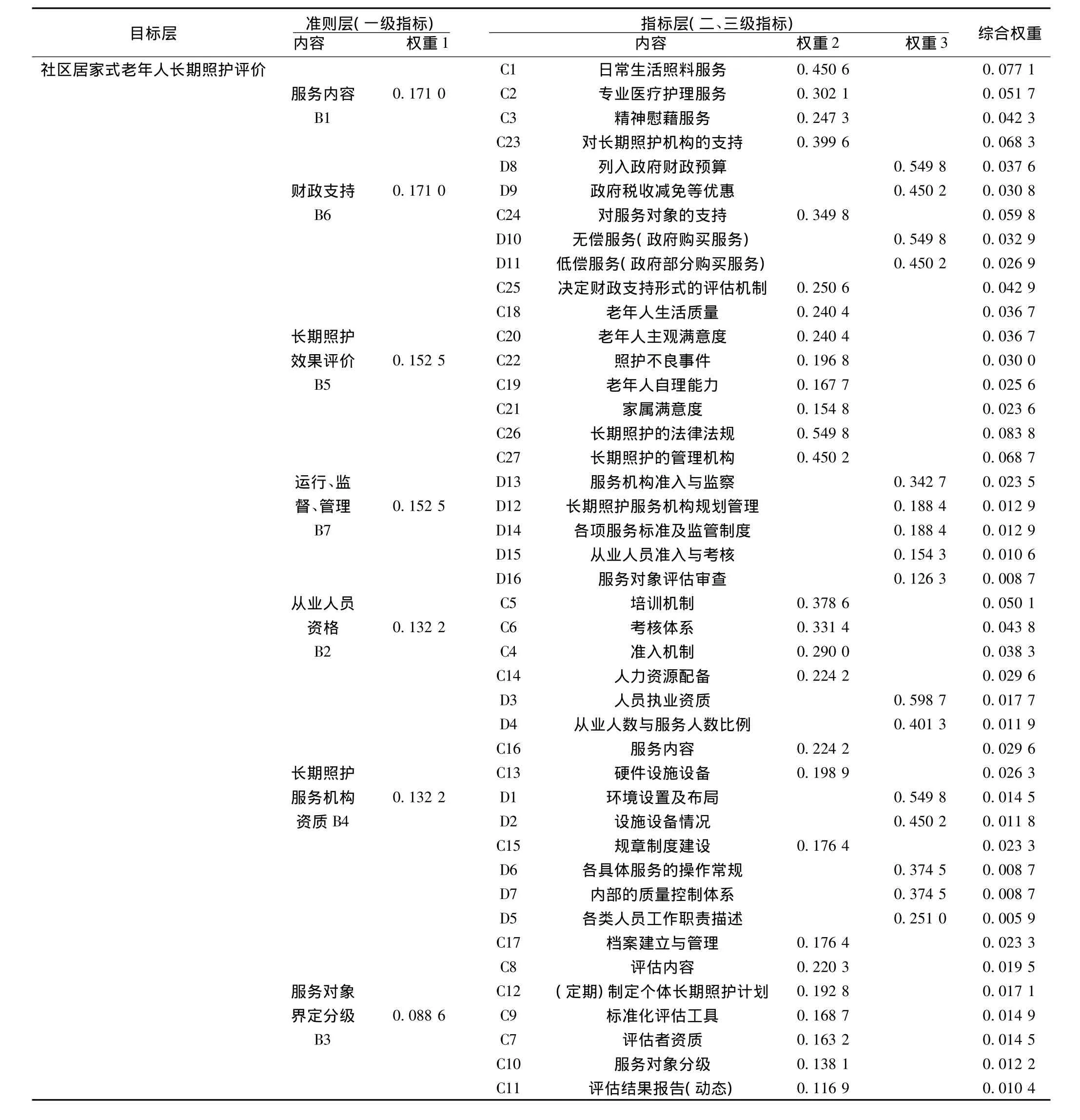
表10 社區-居家式老年人長期照護評價指標體系及其權重

3 討論

3.1 AHP法 AHP法具有系統性、實用性、簡潔性、定量與定性相結合等優點，其比較、判斷、評價、做出決策的思維過程科學而有效，故為本課題采納，以計算、確定指標權重。AHP法作為建立評價指標體系權重的關鍵環節，雖是基于專家群體的知識、經驗和價值所做的判斷，但它對專家的主觀判斷做了數學處理，使專家對指標體系的主觀判斷以數字的形式表現出來，減少了主觀判斷的偏差，因而更加科學。對于計算出的指標權重，逐一進行層次單排序(下級指標對上級指標影響程度)的一致性檢驗，對于計算出的指標權重，進行層次單排序(下級指標對上級指標影響程度)的一致性檢驗，一致性比率C.R越小，判斷矩陣的一致性越好。一般認為，當C.R≤0.1時，判斷矩陣符合滿意的一致性標準，層次單排序的結果是可以接受的。本研究中，各層次單排序一致性檢驗C.R均≤0.1，說明指標權重結果具有較滿意的一致性，具有較高的可靠性。

本研究沒有進行層次總排序的一致性檢驗。這是因為層次單排序通過一致性檢驗，總排序一致性檢驗一般不會有太大偏離;再者，實際構造判讀矩陣，難以兼顧整體排序的一致性;目前，大多數實際工作，都沒有對整體一致性進行嚴格檢驗，常常可以省略〔5〕。

3.2 各指標權重結果 社區-居家式老年人長期照護評價指標體系的7項一級指標，根據綜合權重進行排序，分別為服務內容、財政支持、長期照護效果評價、運行與監管、從業人員資格準入、長期照護服務機構、服務對象界定分級。其中，排在前兩項的為服務內容、財政支持。該結果提示我們，在構建我國老年人社區-居家式長期照護服務體系的過程中，需要著力完善老年人長期照護服務內容體系，重點解決長期照護產生的巨額費用，這也是影響長期照護得以發展的瓶頸。指標長期照護效果評價、運行與監管作為制約性的指標緊隨其后，一方面表明此二項指標具有的不可替代的重要性，同時，也提示我們在發展老年人長期照護的實踐中，要注重科學發展，加強規劃研究，著眼老年人群，嚴格考核評價。照護機構和從業人員作為長期照護服務的供給主體，與其相關的指標的重要性不言而喻;機構和人員的準入制度和標準的研究是一個長期而重要的課題。服務對象界定分級排序最后，盡管如此，但如果從長期照護服務體系總體來看，該指標是直接影響老年人個體接受具體服務內容項目的因素;此外，考慮到老年人長期照護的巨大需求，對需長期照護的老年人進行界定和分級，對于優化配置和合理利用相對有限的長期照護資源，有著極大的現實意義。

1 高玲芳.對統計綜合評價的幾點思考〔J〕.中國統計，2007;(1):49-50.

2 黃方超，王玉環.社區-居家式老年人長期照護評價指標體系的研究〔J〕.中華護理雜志，2011;46(4):388-91.

3 趙煥臣，許樹柏，和金生.層次分析法:一種簡易的新決策方法〔M〕.北京:科學出版社，1986:30-44.

4 孫振球.醫學綜合評價方法及其應用〔M〕.北京:化學工業出版社，2005:12.

5 王國華，梁 樑.決策理論與方法〔M〕.北京:中國科學技術大學出版社，2006:54-76，125-35.