轉管機槍外彈道特性分析與射表計算軟件研究
張開耀,王永娟,徐誠,劉力力,劉國慶,袁輝
(南京理工大學機械工程學院,南京 210094)
0 引言
轉管武器由多根身管環(huán)狀排列而成,通過身管尾和身管頭部箍固定在一起,組成身管組,轉管武器的身管還沿身管膛軸線向中心軸傾斜,形成錐形布置。各身管繞回轉中心軸快速旋轉,輪流到達固定的擊發(fā)位置擊發(fā)射擊,射速可高達3 000~6 000 r/min,對飛機或導彈形成有效的攔截。轉管武器解決了射速高、壽命長、后坐力小三者之間的矛盾,但是目前的研究狀況來看,轉管機槍的外彈道特性并沒有比較精確的分析結果。由于轉管武器身管的轉動帶動膛內彈丸一起運動,彈丸出膛時的運動狀態(tài)與普通槍彈的情況不完全相同,這也給解算帶來了新的問題[1]。
1 槍管旋轉給彈道解算帶來的新問題
1.1 計算模型考慮槍管轉動對彈丸運動的影響
傳統(tǒng)的槍械的基本射表編制方法只對身管靜止時適用,未考慮身管旋轉因素。由于身管旋轉,使彈丸出膛口時的實際速度與身管不旋轉時的情況不同,所以在進行轉管武器的彈道解算應用基本射表的同時,還必須對轉管的影響加以校正。
身管旋轉帶動彈丸旋轉而產生的離心慣性力和科氏慣性力形成對彈帶中心的力矩,同時會產生切向速度和向心速度。
1.2 實際射擊時無法確定射角、射向和受力
轉管武器主要用于近距離防空反導作戰(zhàn),既需要高射又需要平射,無法用傳統(tǒng)方法指示彈道,因此不能用通常的高炮射表編制方法進行試驗測定。由于轉管武器身管錐角的存在,使得彈丸出膛口時轉管武器擊發(fā)管與中心軸的指向不一致,這也需在火控解算中加以考慮[2]。
身管旋轉帶動彈丸旋轉而產生的離心慣性力和科氏慣性力形成彈帶中心力矩使彈丸的初速方向相對身管組中心線形成偏離。這種偏差最終將形成散布,影響射擊精度,計算轉管武器外彈道時應加以修正。
2 身管排列與轉動對初始狀態(tài)的影響
2.1 轉管武器排列錐角對彈丸初始狀態(tài)的影響
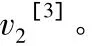


圖1 轉管武器環(huán)形排列示意圖
2.2 身管轉動對彈丸初始狀態(tài)的影響
沿轉管回轉中心向前看截面圖如圖2所示。圖2中,O為坐標原點,逆時針轉過的角度為φ。身管轉動速度為ω,旋轉半徑r,彈丸出膛口時沿圓周的切向速度v3=rω。
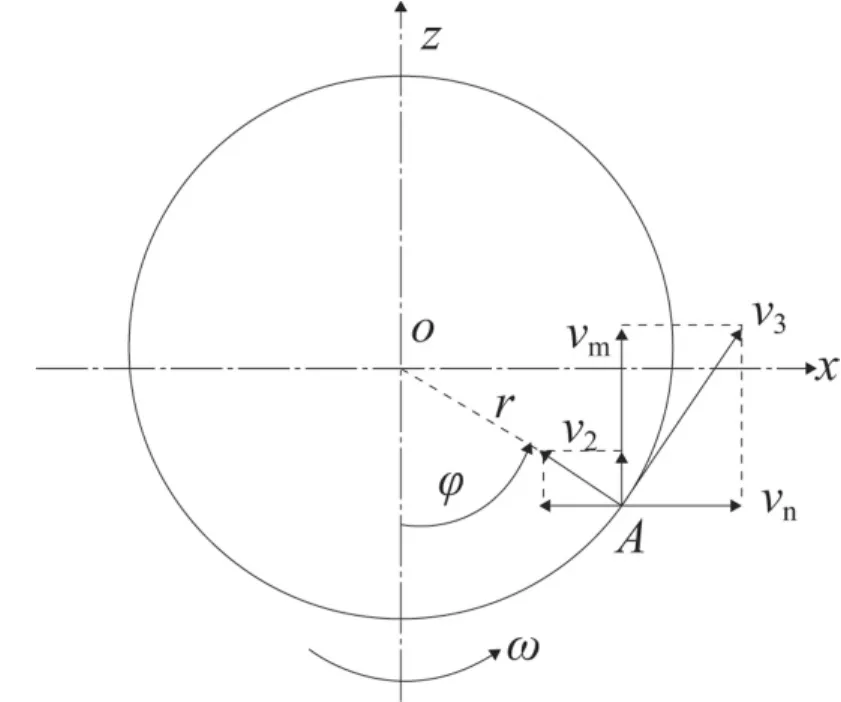
圖2 轉管武器轉管膛口截面
將速度v2和v3在此平面進行坐標分解:
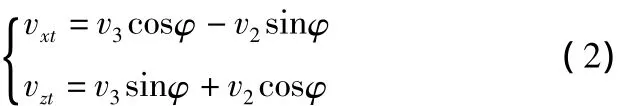
2.3 身管直角坐標系到地面直角坐標系轉換
彈丸初速度以身管直角坐標系o-xtytzt為依據進行計算,彈丸外彈道計算是要以地面直角坐標系o-xyz為依據,因此要對身管坐標和地面坐標進行相應的坐標轉換[3]。
地面坐標系o-xyz中彈丸位置坐標為(x,y,z)T。身管直角坐標系o-xtytzt中位置坐標為(xt,yt,zt)T。
利用旋轉矩陣T將身管坐標系轉換為地坐標系:
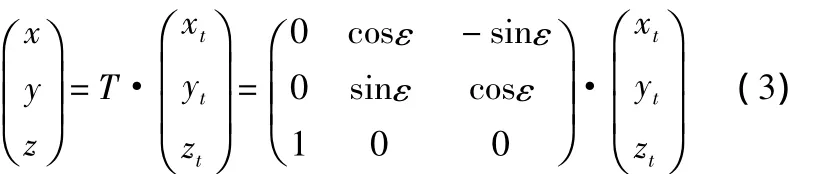
ε為高低角。
身管直角坐標系o-xtytzt中初始速度分量:

經轉換矩陣T坐標變換后彈丸初始速度在地面直角坐標系o-xyz中的初始條件:

身管直角坐標系中彈丸的位置坐標分量:

經轉換矩陣T坐標變換后彈丸初始位置在地面直角坐標系o-xyz中的初始條件:

將上述轉換為地面坐標系中的速度初始坐標分量和位置坐標分量作為彈丸外彈道微分方程的初始值代入外彈道計算模型進行計算。
3 轉管武器外彈道計算模型
從彈丸外彈道微分方程上的初值問題進行建模,提高轉管武器諸元解算的精度,降低模型所引起的“計算”誤差[4]。轉管修正外彈道數學模型由一組微分方程組表征,選用外彈道 4D 微分方程組[5-7]:
初始條件為(t=0):
(x0,y0,z0)和(vx0,vy0,vz0)即為式(5)和式(7),

式中:

H(y)為空氣密度函數

d為彈丸直徑(m),q為彈頭重(kg),
G(vrτ)為空氣阻力函數,
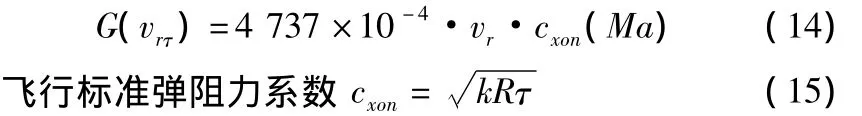
vrτ為彈丸相對空氣速度;vx為地面直角坐標系x方向速度;vy為地面直角坐標系y方向速度;vz為地面直角坐標系z方向速度;i為彈形系數;為彈丸自轉角速度(rad/s);τ0n為標注氣象條件值取 288.9°K;τ為實測溫度+273.15°K;K為常數;R為氣體常數;τ為虛溫;飛行馬赫數Ma=vrτ/c0(速度/音速);Wx、Wy為縱風、橫風速度;θ0為射角,即上述轉管夾角μ;φ為轉管位置與過中心軸豎直坐標之間夾角。
4 不同轉速對彈道特性的影響
標準氣象條件[8],即氣溫取標準氣溫t0=+15℃,地面標準虛溫 τ0b=288.9,標準濕度e0b=6.35 mmHg,地面標準氣壓h1=743.65 mmHg,Wx0=0,Wz0=0。假設轉速為 0,給定射角θ0,表定初速度v0,積分標準氣象條件下的外彈道方程組到落點,得到落點坐標(xt,yt,zt)T和落點速度(vxt,vyt,vzt)T以及飛行時間T。計算得到彈道基本諸元。
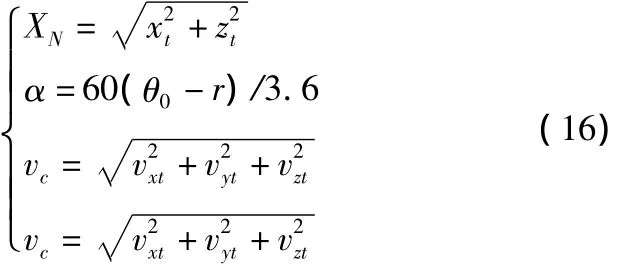
式中r為表定跳角。由式(16)計算得出射距瞄準角α、落速vc,落角θc,最大彈道高Y插值計算得到。
轉速變化時,將不同轉速下的初始條件代入計算方程,積分標準條件下的彈道方程組[9-10]。各轉速的彈道諸元比較計算,得出不同轉速下的彈道特性。
5 轉管外彈道特性計算實例與軟件研究
綜合上述各條件,利用MATLAB軟件對彈道修正的數學模型進行編程計算,并設計計算軟件,繪制計算結果圖形。
以某軍用14.5 mm轉管機槍為例進行計算,初始條件:彈道系數:c=1.6;縱風速度(m/s):Wx=5;橫風速度(m/s):Wz=5;彈頭直徑(mm):d=14.5;地面溫度(℃):T=15;發(fā)射角:θ0=0.5°;初速度:v0=980 m/s;速度變化量(m/s):Δv=10;氣壓變化量(mmHg):Δh=11.2;溫度變化量(℃):Δtb=10;藥溫變化量(℃):Δτb=10;藥溫修正系數Lt=0.001 3,轉速 1 000 r/min。
輸出的彈道諸元計算結果:落點距(m):S=1 390;飛行時間(s):T=1.67;落點速度(m/s):Vt=722;頂點高度(m):Hmax=3.3;落點角度:Thld= -0.615°,縱風修正量1.796 m;橫風修正量0.844 密位;橫向偏移量 13.103 m,繪制本例轉管武器外彈道計算結果如圖3(a-f)。

圖3 轉管武器外彈道計算結果
在其他外界條件相同的條件下,改變轉管轉速為2 000 r/min和3 000 r/min,計算結果與轉速為1 000 r/min主要結果進行比較,如表1所示。
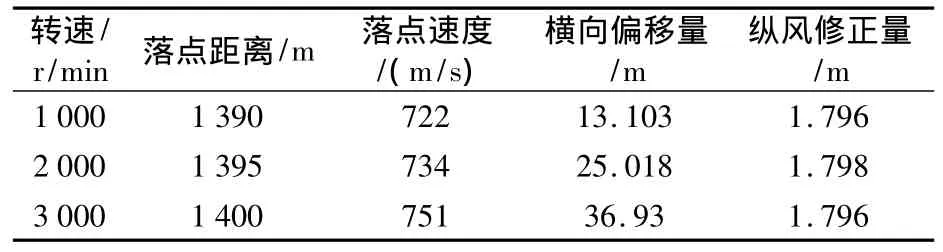
表1 不同轉速下彈道計算結果比較
由圖3可以看出,各圖形數據符合彈丸外彈道特性。通過標準環(huán)境條件與非標準環(huán)境條件下計算結果的比較可以較為精確的得到距離修正量、高低修正量和方向修正量。以彈道諸元計算結果和各修正量為基礎編制轉管武器基本射表和彈道條件變化的修正量表。
6 結語
以外彈道微分方程作為基礎建立了轉管武器修正的數學模型,并對彈丸出膛口時的牽連運動進行分析。本文考慮轉管坐標系和地面坐標系的坐標變換,將地面坐標系位置和速度量作為微分方程的初值,有效地解決了轉管計算修正的問題。
考慮風、氣溫以及氣壓變化情況下建立的轉管彈道數學模型,計算中對各氣象因素綜合考慮,準確有效地得出轉管武器外彈道的偏移量和距離修正量,為轉管武器的射表編制提供了有力的依據。
[1]徐國亮,王茂林.速射轉管炮射擊校正方法[J].火力與指揮控制,2005,30(4):95-96.
[2]韓子鵬,王中原,舒延春.轉管炮射表編制方法研究[J].兵工學報,2002,23(3):304-307.
[3]張保山,陳群齋,李敏.小口徑艦炮轉管修正彈道數學模型研究[J].艦船科學技術,2008,30(3):152-154.
[4]謝鋒,劉樹華,馬江飛,等.轉管武器外彈道特性的分析與計算[J].機械管理開發(fā),2005,5(86):15-16.
[5]浦發(fā).外彈道學[M].北京:國防工業(yè)出版社,1989.
[6]《步兵自動武器及彈藥設計手冊》編寫組.步兵自動武器及彈藥設計手冊[M].北京:國防工業(yè)出版社,1977.
[7]徐勁祥,祁載康,林德福,等.火箭炮射表編擬及發(fā)射諸元快速裝定研究[J].南京理工大學學報(自然科學版),2004,28(3):333-336.
[8]閆章更,祁載康.射表技術[M].北京:國防工業(yè)出版社,2000.
[9]K.B.MNXANJIOB,李芳新.射表編制[M].北京:中國人民解放軍軍事工程學院,1957.
[10]李偉如.射擊與命中的科學[M].北京:兵器工業(yè)出版社,1994.

