雙腔室空氣彈簧的實驗建模

武文山，周振華，金建新

(華中科技大學數字制造與技術國家重點實驗室湖北武漢430074)

0 引言

隨著超精密測量和制造技術的發展，由于精度的不斷提高對環境振動的要求越來越嚴格［1］，隔振系統已經成為超精密測量和制造設備必要的一部分。對于隔振系統的低剛度、高衰減率的要求也越來越嚴格［2］。

超精密隔振系統的關鍵部分是空氣彈簧，相比其它機械式和橡膠式的隔振器，空氣彈簧的優點是利用空氣的可壓縮性實現以較小的剛度支撐起較大載荷。雙腔室空氣彈簧因為具有較低剛度和良好的阻尼特性的優點，而廣泛應用在各種隔振系統中［3］。

圖1所示為雙腔室空氣彈簧隔振器的原理圖，其基本結構為通過一個節流孔連通上下兩個腔室。空氣彈簧的上方由一個剛性的活塞來支撐載荷(包括隔振平臺和精密設備)，活塞和上腔室壁之間通過安裝橡膠密封膜來防止空氣泄漏。

圖1 雙腔室空氣彈簧隔振器原理圖

為了使空氣彈簧隔振系統達到更優越的性能，結構參數優化和主動控制是兩種有效的方法［4-6］，而這兩種方法的應用都需要事先獲得空氣彈簧的精確數學模型。Shearer通過考慮腔室的熱力學過程得到了空氣彈簧的非線性模型［7］，Harris和Debra在活塞小位移運動的條件下推導出了線性模型［8，9］，但是其理論模型與實際測試數據之間存在較大差異。本文在實驗的基礎上分析差異存在的原因，將密封膜的影響考慮在模型內，并通過參數識別得到改進模型的傳遞函數。

1 空氣彈簧的理論模型

要獲得空氣彈簧的理論模型，就是要建立輸出量(活塞板的運動xp)對輸入量(地面擾動xbase、干擾力Fd)的傳遞函數表達式。

雙腔室空氣彈簧在工作時，可認為活塞在其靜態平衡位置附近作微幅運動。微幅運動過程中所產生的動態力引起上腔室中空氣質量(mt)、壓力(Pt)、體積(Vt)、溫度(Tt)、節流孔中氣流(mtb)，以及下腔室空氣質量(mb)、壓力(Pb)和溫度(Tb)的變化，各變化量如圖2所示。由于這一過程速度非常快，可近似視為絕熱過程。根據能量交換可作出以下推導。

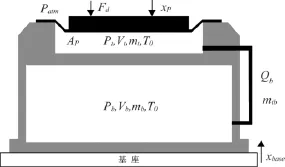
圖2 變量示意圖

1.1 腔室空氣質量的變化

對于上腔室，使用開口系統的能量方程［10］：

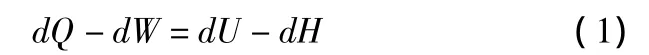
其中，dQ為系統吸收(放出)的熱量，對于絕熱過程dQ=0;dW為系統所作的膨脹功，在小位移條件下有dW=P0dVt;dU為熱力系自身能量的變化，其表達式如下：

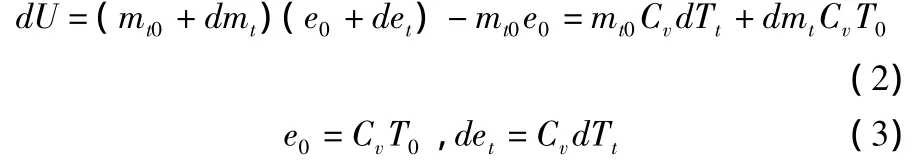
dH在此處為空氣流入節流孔引起上腔室焓的變化，因此有：dH=dmtCpTtI，其中TtI為節流孔在上腔室入口處的溫度;e0和det分別代表初始內能和內能的變化量;Cp和Cv分別為等壓比熱容和等容比熱容;將式(2)、式(3)及dW、dH的表達式代入式(1)中，得到：

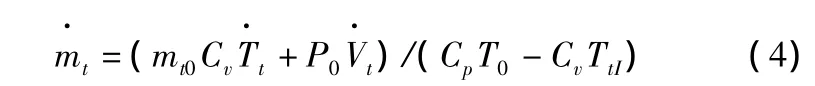
根據shearer的理論，在小位移情況下，節流孔中的溫度變化可以忽略不計，故有TtI=T0。將腔室中的氣體假設為理想氣體，因此有：

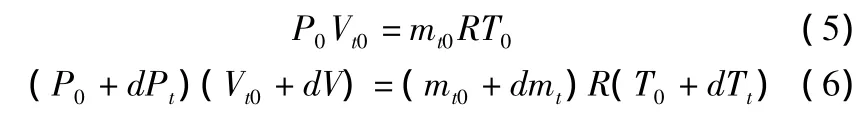
由式(5)和(6)，得到腔室中空氣的質量、體積、壓力和溫度之間的變化關系式(7)，將式(7)代入式(6)中，得到式(8)。

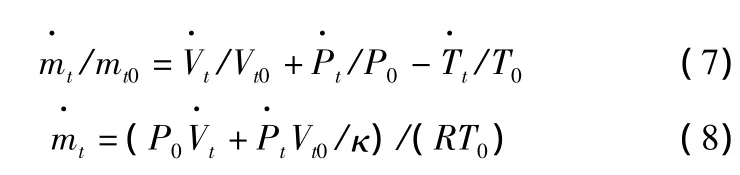
其中，κ為比熱比κ=Cp/Cv。對于下腔室，類似地有：

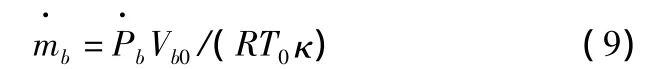
1.2 節流孔中的質量流速

對于節流孔，設經過氣管進入到下腔室的流量為Qb，節流孔中的質量流速為，則有下述關系：

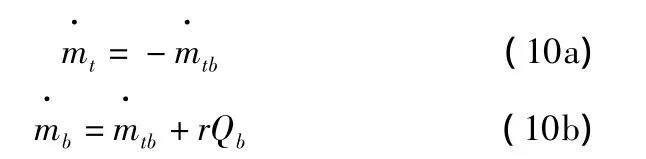
根據細長孔(l/d＞4)的壓力流量特性：

q=pd4Δp/(128 ml)，得到：

其中，Cr為流量系數，Cr=pd4/(128 ml)，μ為空氣粘度。

1.3 傳遞函數

對活塞，應用牛頓第二定律，得到：

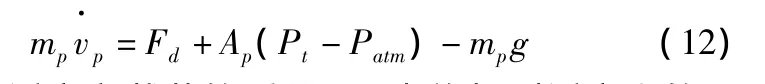
其中，mp為活塞和載荷的質量;Fd為施加到活塞上的干擾力;Ap為活塞的有效面積;vp為活塞的運動速度;Patm為外界大氣壓;Vt為上腔室的體積，其表達式為：

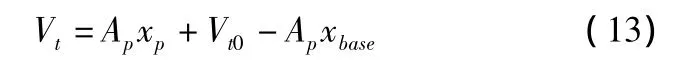
將式(11)代入式(10a)，再代入式(8)，并將式(13)代入式(8)得到：

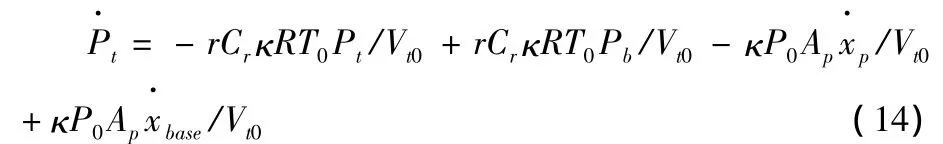
由于活塞可視為在靜態工作點附近做小幅運動，其振動幅值范圍為0～20 μm，故可以將其線性化：

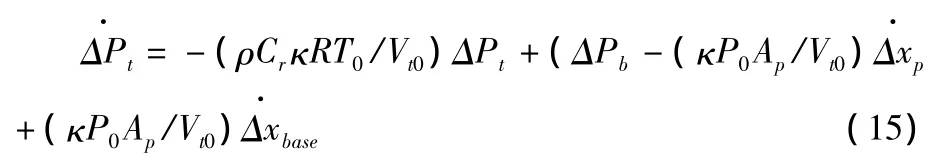
同理，將式(11)代入式(10b)，再代入式(9)，得到：

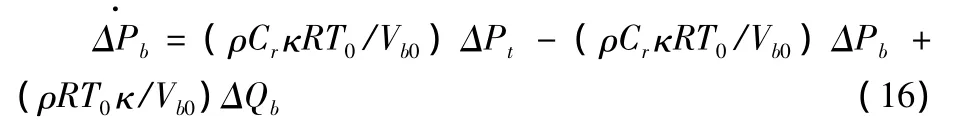
由式(12)可得：

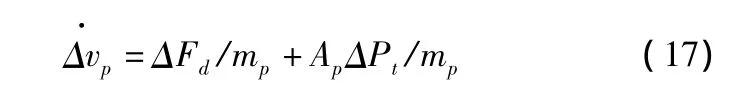
對方程式(15)、式(16)、式(17)進行拉普拉斯變換，可得：

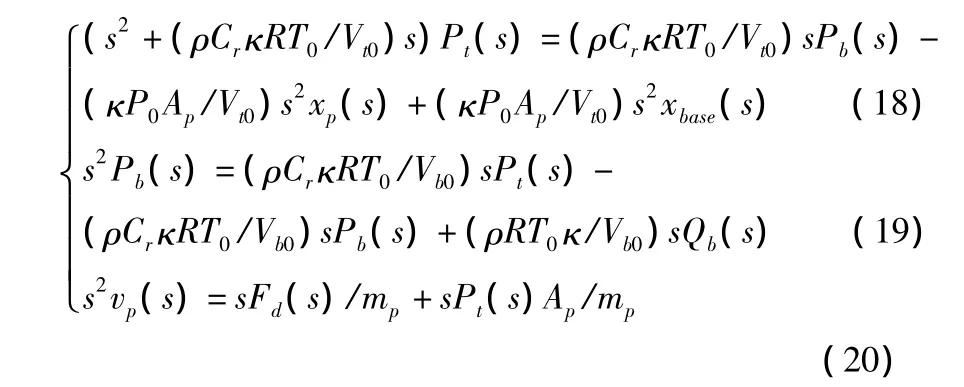
聯立式(18)、式(19)、式(20)三式，可得傳遞函數：

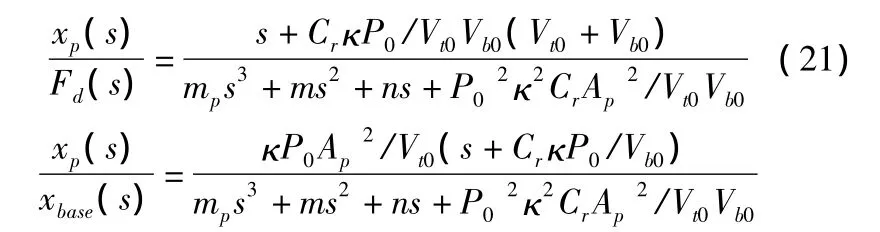
其中：

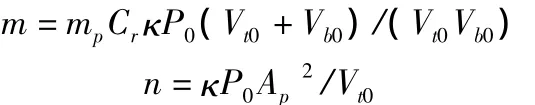
2 模型檢測實驗與分析

2.1 實驗設計及結果

一個可使用的數學模型需要能夠精確地預測系統的特性，為了檢測空氣彈簧理論模型的有效性，將理論傳遞函數與實測數據進行對比。

圖3為實驗裝置簡圖，其包括空氣彈簧、音圈電機、傳感器、數據采集器及PC主機。使用NI測控系統控制音圈電機對空氣彈簧的活塞板進行激勵，由動態力傳感器獲得激振力信號，速度傳感器獲得空氣彈簧的速度響應(速度傳感器安裝在活塞板上)，傳感器采集到的信號經過調理后進入LMS數據采集系統，然后由軟件進行頻譜分析得到響應速度對激振力的實測傳遞函數。

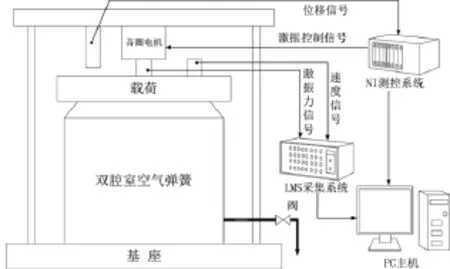
圖3 實驗裝置圖

實驗采集的輸出量為活塞板的速度，其對激振力的理論傳遞函數可由式(21)經變換得到：

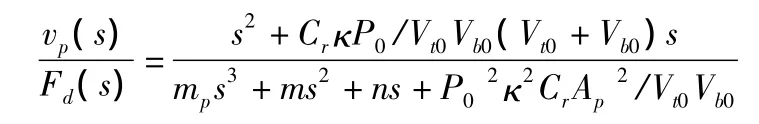
實驗測得傳遞函數與理論傳遞函數的對比如圖4所示。可以看到，共振峰出現的位置及峰值的大小均存在較大的偏差。理論傳遞函數中，系統的共振頻率為1.76 Hz，而實測曲線表明共振頻率為2.64 Hz。

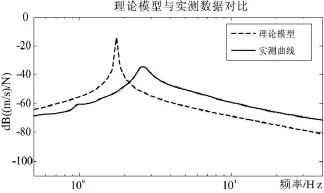
圖4 實測傳遞函數與理論模型對比

2.2 實驗結果分析

理論傳遞函數和實測曲線之間共振頻率和共振峰存在偏差，表明理論模型對系統實際剛度和阻尼的預測不準確。在理論模型中，系統的剛度主要由空氣彈簧腔室的尺寸和載荷大小決定，阻尼主要由節流孔的尺寸決定。在圖3所示的實驗裝置中，以上相關尺寸都是確定已知的。在建模過程中，唯一沒有考慮的元件是橡膠密封膜，因此需要重新考慮其對系統剛度和阻尼的影響，進而對模型進行修正。

密封膜的材料為中間加入一層滌綸布的丁腈橡膠，由于橡膠結構件可能引入非線性影響，因此需要進一步探究密封膜對空氣彈簧的影響是否與激振條件有關(激振的幅值、頻率等)。文獻［4］的研究表明節流孔具有非線性的特性，因此為了消除節流孔的影響，設計了圖5所示的單腔室實驗。圖5(a)為空氣彈簧的單腔室裝置圖(去掉節流孔，將上下腔室打通)，圖5(b)為逐漸增加激振力的幅值大小(從0.02到0.14)測得的一系列傳遞函數。可以看到，在激振幅值變化時，傳遞函數曲線基本上是重合的。因此可以得出結論，在該實驗條件下，密封膜的剛度和阻尼可視為常值。

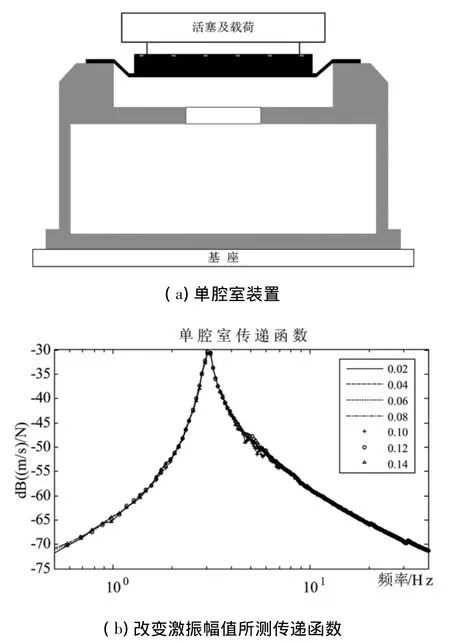
圖5 單腔室實驗

3 空氣彈簧的改進模型

3.1 改進模型的提出

根據第2節的實驗結果及分析，將密封膜的模型簡化為彈簧(Km)、粘性阻尼(Cm)與結構阻尼(Cd)的組合。對于結構阻尼，其應力－應變曲線為一個滯后回線。此回線所圍的面積表示一個循環中單位體積的材料所消耗的能量，這部分能量以熱能的形式耗散掉，從而對結構的振動產生阻尼。材料阻力在一個周期內所消耗的能量ΔEs與振幅的平方成正比，而在相當大的范圍內與振動頻率無關［11］，即有：

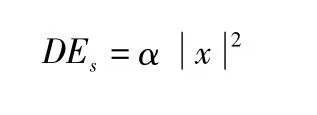
在小振幅的條件下(＜20 μm)，這部分的影響可以忽略不計，因此密封膜對模型的影響可以等效為彈簧(Km)加粘性阻尼(Cm)，如圖6所示。

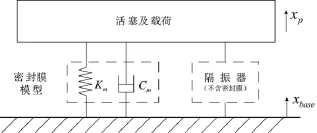
圖6 考慮密封膜的模型

在考慮密封膜的影響后，活塞板的動力學方程為：

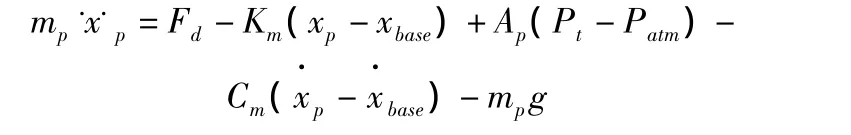
對上式進行拉普拉斯變換可得：

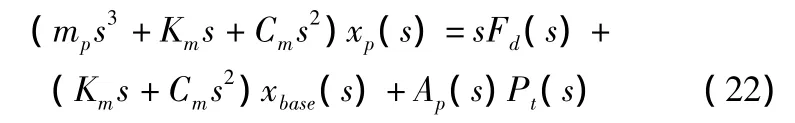
聯立求解式(18)、式(19)、式(22)，可得修正后的傳遞函數為式(23)，其中Km，Cm為未知參數，可通過參數識別確定具體值。

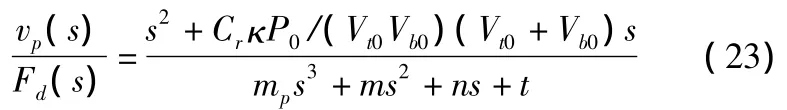
其中：

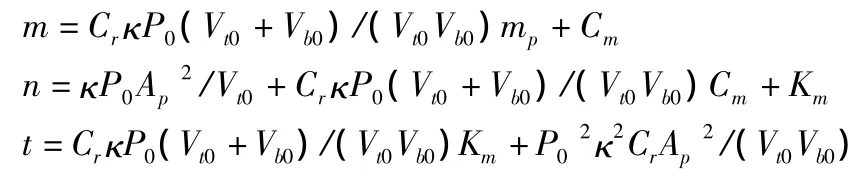
3.2 參數擬合

由于理論模型中，節流孔的流量系數Cr為經驗公式，因此在參數識別中，將Cr作為未知參數處理。

參數擬合采用麥夸特算法，即阻尼因子法，其基本思想是在高斯－牛頓算法中得到的矩陣A中加一項阻尼因子，其收斂性優于高斯－牛頓法，在計算初值較差的情況下仍較易收斂。使用1stOpt軟件編制相應程序進行參數擬合，表1為軟件運算收斂后各優化評價參數的值。

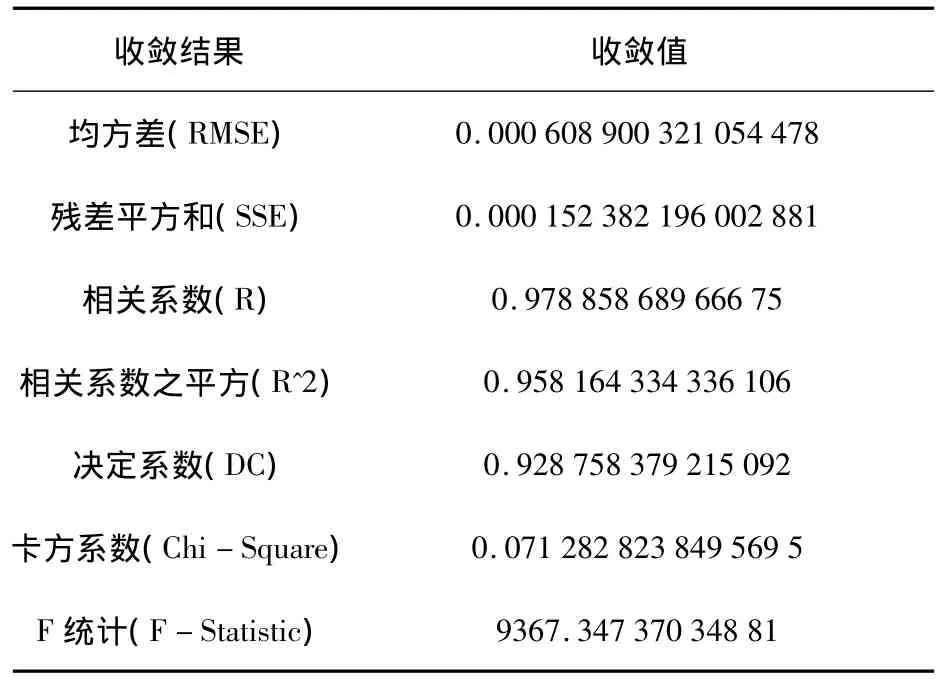
表1 參數優化結果

最終得出Km和Cm的最佳估算值為：

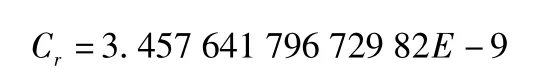
將最佳估算值代入到式(23)中得到改進模型的傳遞函數，將其與理論模型及實測曲線進行對比，如圖7所示。可以發現，在考慮了密封膜結構的影響之后，與理論模型相比，改進模型更接近實測曲線。其中在共振峰附近改進模型與實測數據有較高的擬合度，而在較低頻段及較高頻段，改進模型仍不能較好地吻合實驗數據。其中一個重要原因是節流孔的阻尼特性尚未有成熟的理論公式，文獻［4］研究了節流孔的開口大小對阻尼的影響，而該實驗結果也可作為進一步研究節流孔阻尼機制的參考。

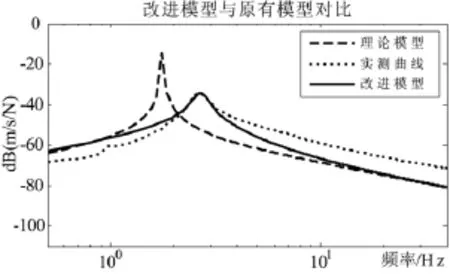
圖7 改進模型與理論模型對比

4 結論

雙腔室空氣彈簧理論模型與實測數據之間存在較大的差距，本文在實驗數據的基礎上分析了橡膠密封膜對空氣彈簧模型的影響，通過對實驗數據進行分析，將密封膜簡化為一個彈簧和一個阻尼并聯。將密封膜的剛度和阻尼作為未知參數建立新的模型，通過參數優化得到未知參數的值，改進模型與原有模型的對比表明了改進模型的有效性。由于節流孔的阻尼機制尚未清晰，因此本模型具有一定的局限性。

［1］C.G.Gordon，Generic criteria for vibration－sensitive equipment［C］//Proceedings of SPIE，San Jose，CA，1991.

［2］Eric H.Anderson，Bowie Houghton，ELITE－3 active vibration isolation workstation［J］.Smart Structures and Materials2001：Industrial and commercial applications of smart structures technologies，2001，pp.183 –196.

［3］Cyril M.Harris，Allan G.Piersol，Harris’Shock and Vibration Handbook，5th Edition［M］.McGraw － Hill，2001.

［4］Jeung－Hoon Lee，Kwang－Joon Kim，Modeling of nonlinear complex stiffness of dual－chamber pneumatic spring for precision vibration isolations［J］.Journal of Sound and Vibration301(2007)909–926.

［5］ Abu Hanieh.Active Isolation and Damping o f Vibrations via Stewart Platform［D］.Brussels：ULB Active Structures Laboratory，2003.

［6］Yoshioka H，Takahashi Y，Katayama K.An Active Microvibration I-solation System for Hi－ tech Manufacturing Facilities［J］.Journal of Vibration and Acoustics，2001，123：269 －275.

［7］J.L.Shearer，Study of pneumatic processes in continuous control of motion with compressed air［C］//Transactions of ASME78(1956)233－242.

［8］ C.M.Harris，C.E.Crede，Shock and VibrationHandbook［M］.McGraw －Hill，New York，1961.

［9］ D.B.Debra，Design of laminar flow restrictors for damping pneumatic vibration isolators，CIRP Annals33(1)(1984)351－356.

［10］黃曉明，劉志春，范愛武.工程熱力學［M］.武漢：華中科技大學出版社，2011.

［11］師漢民.機械振動系統－分析·測試·建模·對策［M］.武漢：華中科技大學出版社，2004.