漸進成形機床床身結構分析與優化設計

孔波，周燕飛

(南京航空航天大學機電學院，江蘇南京210016)

0 引言

近年來，隨著科技快速發展，機床設計領域逐步由傳統設計向現代設計過渡。目前，國內機床結構的一般設計過程為：根據設計要求進行半經驗半理論的傳統設計，完成三維CAD繪圖，然后對初步設計進行CAE分析，進而根據分析結果進行再設計再優化;如此反復，直至性能達到要求，最后才進行加工制造。在進行CAE分析時，如何根據結構的不同特點選取與之匹配的現代設計方法對其進行優化，從而有效提升機床的性能指標，成為近年來研究的熱點［1］。

機床床身結構是機床關鍵的基礎部件，起著支撐工作臺、立柱等關鍵零部件的作用。其靜動態特性對機床的加工精度和效率起著至關重要的影響。床身的靜動態性能集中體現在靜力學性能和低階模態特性上。因此，以大型CAE分析軟件ANSYS Workbench 13.0為平臺，用有限元的方法，在床身結構動態特性靈敏度分析的基礎上，對用傳統設計法設計的金屬板料漸進成形機床進行了靜力學性能分析和模態分析，實現機床結構與動態性能優化。該方法可以推廣到機床其他部位的結構優化中，從而為機床結構的改進、機床的優化設計提供了重要的方法。

1 結構特點與受力分析

在分析及優化之前，要搞清楚該機床床身本身的結構特點及其與外界是如何連接的，從而得出正確的約束和受力，進而為有限元分析前處理提供正確的前提條件。圖1、圖2為床身的結構示意圖。

圖1 床身的結構示意圖(正面)

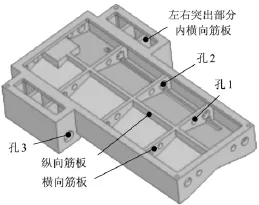
圖2 床身的結構示意圖(反面)

1.1 結構特點

該機床裝配完成后，床身底部四個角會有4個頂尖支撐。上部有導軌安裝面、左右立柱安裝面、y向伺服進給系統安裝面。床身內部為縱橫交錯的筋板結構，筋板數量為3行×1列，每塊筋板及前后壁上都開有4個減重孔。

1.2 受力分析

床身在靜力狀態下工作時，除自身重力外，導軌安裝面上受到其上兩根滑軌、4個滑塊、工作臺、升降臺部件、加工工件的重力(F1)作用;傳動絲杠安裝面受到其上y向伺服進給系統重力(F2)作用;左右立柱安裝面受到其上立柱、橫梁、z向伺服進給系統、z向托板、電主軸、鉆夾頭、成形工具頭等重力(F3)作用。

2 有限元模型的建立

利用ANSYS Workbench 13.0和三維軟件SolidWorks良好接口關系，首先在SolidWorks中，要將模型進行一定的簡化，即忽略小的倒角、圓角和對結構性能影響不大的小尺寸［2］，然后直接導入 ANSYS Workbench 13.0 中，從而完成幾何模型的轉換。選用Workbench中Static Structure(ANSYS)模塊進行有限元模型的進一步建立。首先定義材料屬性，在Engineering Date中定義材料屬性，該機床床身材料為灰鑄鐵，密度為7 200 kg/m3，彈性模量為1.1×105MPa，泊松比0.28。定義完材料屬性后，在model子模塊中進行網格劃分。劃分時，充分利用ANSYS Workbench對大部件的自動劃分功能。劃分完成后，就建立起了該床身有限元模型。機床床身模型劃分單元數36 254個，節點數59 615個，有限元模型圖如圖3所示。

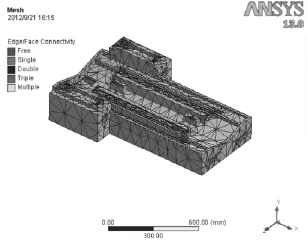
圖3 床身有限元模型圖

3 床身分析

3.1 靜力分析

床身靜力學性能主要是考慮在最大外載荷的情況下，床身的變形能力，即靜剛度。

1)施加載荷和約束

對已經建立起來的有限元模型進行前處理即施加載荷和約束。首先施加邊界條件和約束，對于床身底部4個角與頂尖結合處為圓心、半徑為5的4個圓形面施加全約束。其次，加載床身自身的重力作用。最后，施加F1，F2，F3。床身受力和約束示意如圖4所示。

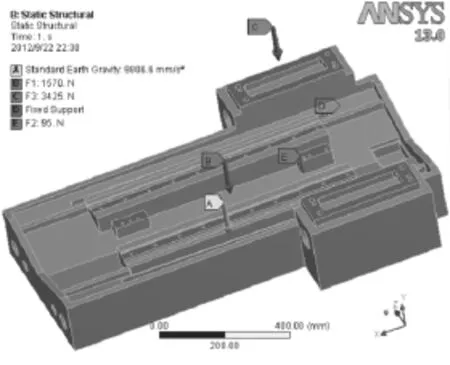
圖4 床身受力圖

2)求解

經過正確的前處理，加載合適有效的約束和作用力，既可以進行求解。求解出的總變形量最大值為3.67×10－2mm、平均(von－Mises)應變最大值 1.245 1 ×10－4、平均(von－Mises)應力最大值為13.696 MPa。

3.2 模態分析

模態是動力學性能的重要參數之一。就床身而言，其低階頻率的高低更能反應該部件的性能。為了保證模態數據和實際工況的一致性，進行模態計算時，要將實際狀態下約束要素施加在床身上。在ANSYS Workbench13.0平臺中，利用Modal(ANSYS)模塊及Static Structure(ANSYS)模塊中建立起來的前處理模型，將兩者直接連接進行計算，求解得到該機床床身的模態。前4階模態頻率見表1，前4階模態振型為圖5，圖6，圖7，圖8所示。

表1 機床床身前4階固有頻率

圖5 床身一階模態振型圖

圖6 床身二階模態振型圖

圖7 床身三階模態振型圖

圖8 床身4階模態振型圖

3.3 分析結果

分析結果表明床身所受的最大應力13.696 MPa，遠低于床身材料灰鑄鐵的最大需用應力值。床身結構的一階固有頻率為151.52 Hz，與電主軸引起的震源頻率比較接近，容易與外界發生耦合。需要提高床身結構的一階固有頻率。

一階振型為床身的中心部位上下振動。床身中心部位的振動最大。二階振型為中間兩側部位左右擺動。并且立柱安裝面部位的前段扭動最大。三階陣型為床身兩側立柱安裝部位左右在y－z平面內擺動。4階振型為床身兩側在x－y平面內上下擺動。由此可見床身中間部分與兩側部分的連接剛度不夠。

4 床身結構的改進與分析

4.1 床身結構動態靈敏度分析［3］

床身的動態特性靈敏度指模態參數對設計變量的靈敏度，可以用Δf/Δx來表示，其中f為結構的固有頻率，x為設計變量。以動態特性靈敏度分析為依據，對床身進行進一步的優化設計。

4.2 床身結構筋板數目的改進設計

床身結構的改進是針對原始結構在經驗類比的基礎上設計的。內部筋板影響結構動剛度的重要因素［4］。為考察床身不同筋板結構對其動態性能的影響，對其筋板結構進行改進設計。筋板結構的改變包括筋板布局形式的改變及筋板數目的改變。

床身內部筋板結構如圖2所示。采取只改變床身內部筋板數目的改進方案。根據模態分析的結果，擬定3種改進方案：1)改變床身橫向筋板的數目，其他筋板不變;2)改變床身橫向筋板的數目，縱向筋板數目改為2條;3)改變床身橫向筋板的數目，去掉減重孔1(圖1中)，其他筋板數目不變。圖9，圖10，圖11為三種方案床身固有頻率隨著橫向筋板數目增加的變化曲線。

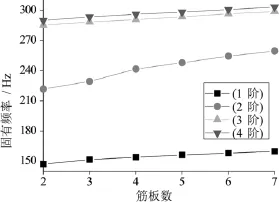
圖9 第1種方案筋板數目對固有頻率的影響

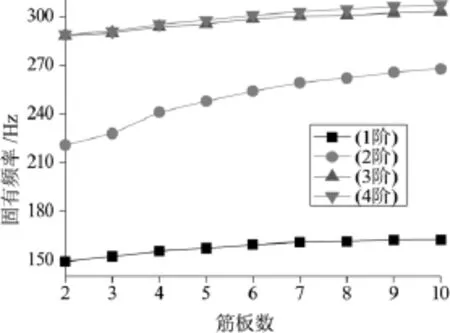
圖10 第2種方案筋板數目對固有頻率的影響

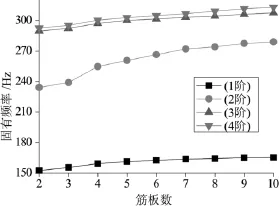
圖11 第3種方案筋板數目對固有頻率的影響

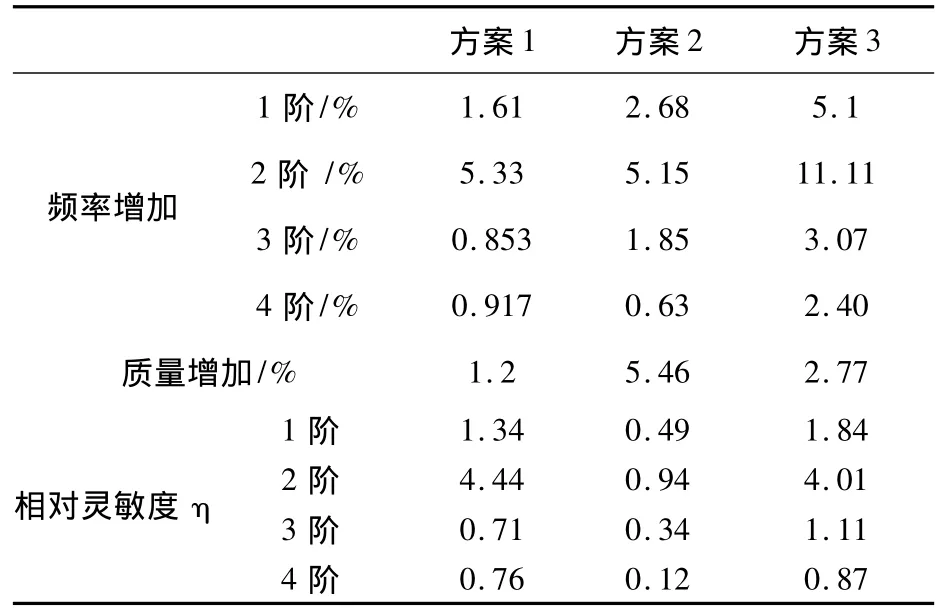
表2 3種方案比較

通過圖9、圖10、圖11可以看出隨著筋板數目的增加，床身各階頻率均有增加。這說明增加筋板的數目，可以提高床身的動剛度。3根筋板數目到4根筋板各階頻率升高的速度最快，超過4根筋板后頻率升高的速度變慢。因此，在保證床身有較好剛度的同時保證材料消耗最少。選取方案1、2、3中的4根筋板數目為各個方案的最優方案。

5 床身結構的進一步改進與優化

選取方案3為結構改進方案繼續進行優化，在保證提高原有結構動態剛度的同時考慮床身質量。設床身質量與模態前 4 固有頻率分別為m，F1，F2，F3，F4，選取床身的前側壁厚、后側壁厚、左側壁厚、右側壁厚、頂面壁厚、底面壁厚、橫向筋板厚、縱向筋板厚、左右突出部分內橫向筋板厚、孔 1 直徑、孔 3 直徑分別為設計變量x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11。并對變量間做關聯處理a1=x1=x2=x3=x4=x5=x6，a2=x7，a3=x8，a4=x9，a5=x10，a6=x11。目標函數為F1＞f1，f1為原有結構的1階固有頻率。根據實際情況，限定各個變量的范圍為：16≤a1，a2，a3，a4≤26，30 ≤a5≤45，40 ≤a6≤65。運用 ANSYS Workbench 優化設計功能模塊，將設計變量a1，a2，a3，a4，a5，a6通過 solidworks傳遞給ANSYS Workbench。經優化后得床身的優化集，選出1階頻率最高的5組作為方案3的最終設計集(見表3)。計算出各組的1階頻率相當于質量的相對靈敏度。可以看出第三組數據質量對1階固有頻率的影響率最高。所以選擇第三組為最終優化設計方案。兼顧床身的動態性能及質量。

從表4中可以看出，優化后的床身結構動態剛度有所增加，并且靜力分析最大變形也有所減小。

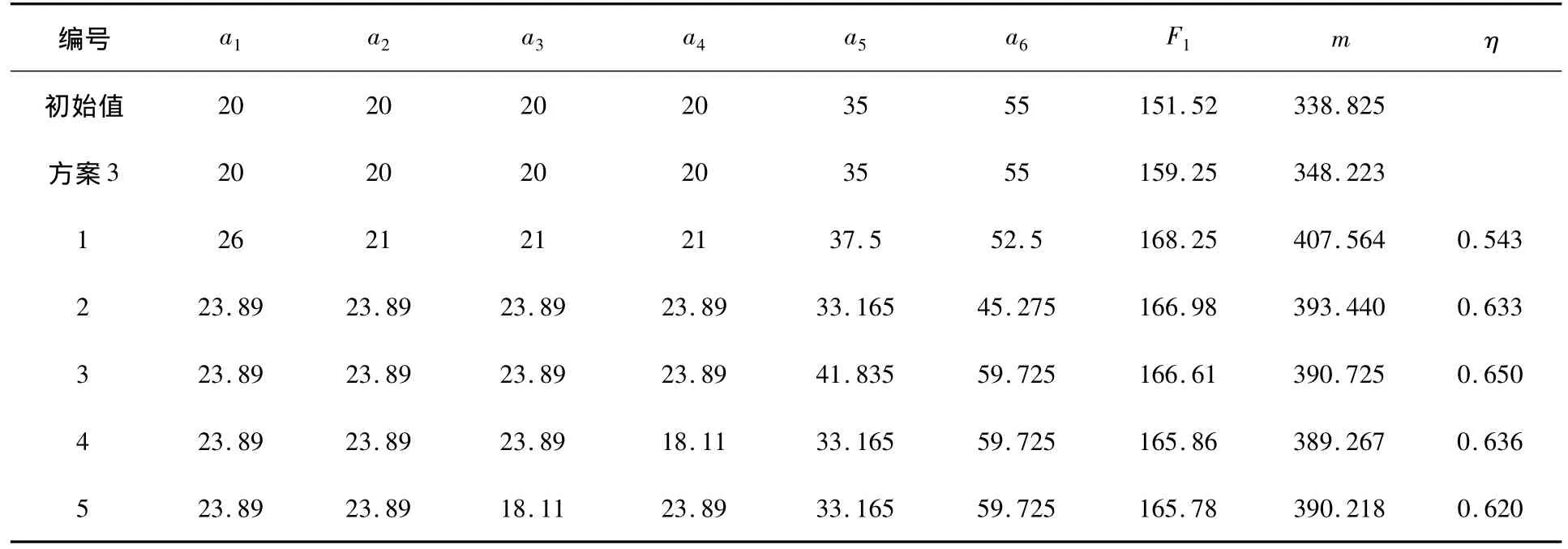
表3 優化方案3設計集

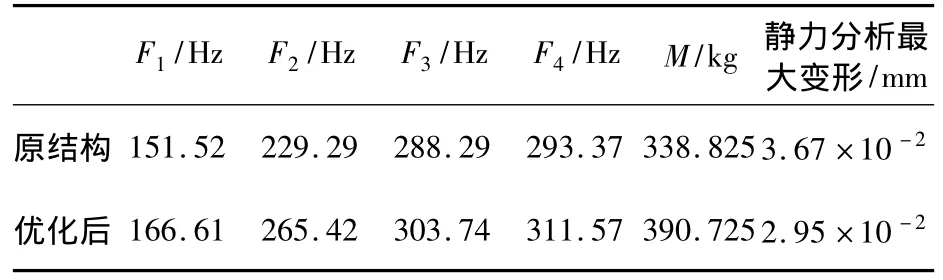
表4 優化后結構與優化前結構對比

6 結論

以Solidworks為設計平臺，以ANSYS Workbench為分析優化平臺，對該機床床身進行了結構分析及優化設計。最終得出以下結論：

1)通過對原始床身的初步分析，發現1階固有頻率較低，以及結構上的不足，擬定了三種不同的改進方案，基于床身結構動態特性靈敏度分析，確定了最優的結構改進方案。避免了設計的盲目性。

2)通過對床身結構參數(包括壁厚、筋板厚、減重孔大小)的優化設計，進一步對床身結構進行優化，列出1階頻率最高的優化集，最后根據床身質量對1階頻率影響的靈敏度分析比較，確定了最終的優化結構，兼顧了動態特性與質量。

3)文中的優化設計方法與步驟可以推廣到機床其他部件的結構優化設計中。本文沒有對床身內部筋板的布局形式進行改進設計，直接進行筋板數目的改進設計。如有必要，設計方法中可以加入床身布局形式的改進設計，然后再對筋板數目進行改進設計。

［1］張強，尹志宏，張明旭，等.基于ANSYS Workbench的大型數控龍門銑鏜床床身靜動態特性分析(J).科學技術與工程.2012，12(1)：182-183.

［2］張明旭，尹志宏，劉曉東，等.結構簡化對模態結果的影響(J).現代制造工程，2008，3(11)：118 －120.

［3］楊勇，張為民，李鵬忠.基于動態靈敏度分析的數控機床床身結構優化設計(J).機械設計.2011，28(9)：49－52.

［4］李小彭，趙志杰，聶慧凡，等.某型數控車床床身的模態分析與結構優化(J).東北大學學報(自然科學版).2011，32(7)：989－991.