基于Pro/E和ADAMS的步行康復器械的動力學仿真與分析

黃玲，陳圓意，吳杰

(南京理工大學機械工程學院，江蘇南京210094)

0 引言

截癱病人喪失站立和行走機能，生活難以自理，不僅給家庭和社會帶來很大的經濟負擔，而且患者自身也承受著巨大的精神壓力和肉體折磨。現今，借助多樣的康復器械產品和中醫康復治療，以及患者長期積極主動的康復鍛煉，能夠有效的促進肢體恢復，降低致殘程度，減少并發癥，增強生活自理能力，恢復對生活的信心，促進其最大限度地回歸社會［1］。

步行康復器械就是一種實用方便的康復器械，尤其對于下肢癱瘓的患者。這款主動型的步行康復器械可以充分利用患者健全的上肢功能，通過手部對轉向機構的控制，配合人體有節奏的左右擺動，實現站立、前進、后退、轉彎等基本的功能。一方面，通過站立、步行康復訓練和簡單的步行等雙下肢的被動訓練，可以促進血液循環，防止癱瘓肢體的神經性水腫、肌肉萎縮和關節攣縮，并可防止因臥床引起的壓瘡、肺及尿路感染、便秘、骨質疏松等并發癥;另一方面，通過雙上肢控制轉向機構和左右擺動的訓練，鍛煉雙上肢肌力和胸腰部的肌肉力量，來代償已喪失的功能，消除和減輕患者功能上的障礙，改善患者的負性情緒和軀體功能狀態，并可提高其生活品質［2］。

1 分析方法的實現

虛擬樣機技術是當前設計制造領域的一項新技術［3］。它是在CAD模型的基礎上把虛擬技術與仿真方法相結合，為產品的研發提供一種全新的設計方法。它可以迅速地分析比較并改進系統的設計方案，提高產品的性能，最大限度地減少物理樣機的試驗次數，提高研發效率。

一種有效的研究方法是應用Pro/E和ADAMS建立步行康復器械的虛擬樣機模型，并通過設置相應的參數，來模擬行走過程中整個人機系統運行的穩定性情況。

2 虛擬樣機模型的建立

1)在Pro/E中零件三維模型的建立和整機模型的虛擬裝配。各個主要零件創建完后，采用自底向上的裝配方式，完成整體的裝配如圖1。建立裝配體時需注意適當的調整和排序，考慮各個構件運動的相對位置關系，從而確定裝配關系和裝配順序，以減少以后的調整。

2)虛擬樣機導入ADAMS中。在Pro/E中安裝Mechanical/Pro［4］接口模塊，將Pro/E中裝配好的三維模型在此接口模塊中定義剛體，設置轉換精度及添加部分約束副等操作后，導入ADAMS中，可以實現無縫連接，并避免一些圖形元素的丟失。

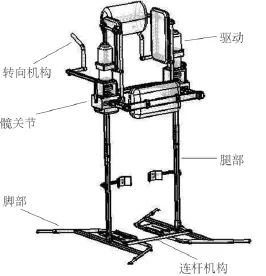
圖1 步行康復器械的裝配圖

3)虛擬樣機模型的修改。完成虛擬樣機的導入工作后，利用ADAMS提供的建模工具，對虛擬樣機模型的部分構件進行修改和完善，添加必要的驅動和約束，定義模型接觸等，完備模型所必需的元素。

4)虛擬樣機模型的檢查。在完成虛擬樣機建模和設置之后，可以對系統的構成、系統的自由度、未定義質量的構件和過約束等情況進行查詢，確保模型的準確性，以便順利進行后續的仿真分析。

3 穩定性步行的邊界條件

在雙足步行研究領域，零力矩點［5，6］(ZMP)理論是被用于步態分析最常用的一個準則。求出穩定步行的邊界條件，為后續仿真結果的比較分析墊定基礎。

下面分別就其邊界條件進行分析。

1)人體質心左右偏移的擺動運動階段

在該階段內，系統質心容許的最大邊界條件為：

t=0 即穩定站立時xc=b/2;

t=T/6即向左擺動時xc= －b0。

其中xc為系統質心相對于左腳豎直支撐桿的水平位移，b0為腳部延長機構墊塊在x軸方向的長度，b為兩支撐腳之間的距離設為550 mm。

為了提高安全穩定性，保證更大的安全裕度，可以適當調整系統的質心在t=T/6時刻的邊界條件，即b0可以適當延長，如圖2。

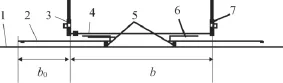
圖2 腳部設計示意圖

2)單腳支撐的步行運動階段

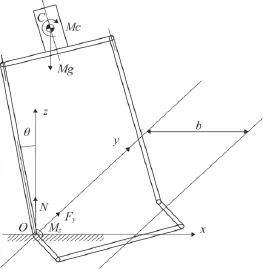
圖3 單腳支撐階段模型圖

為保證步行過程中腳底不打滑，合力應小于地面與底部產生的最大靜摩擦力。設地面和底部的靜摩擦系數為μ，則應滿足：

其中再結合步行康復器械系統質心的牛頓方程和系統相對于步行康復器械質心C點的歐拉方程，求解整理可得到：

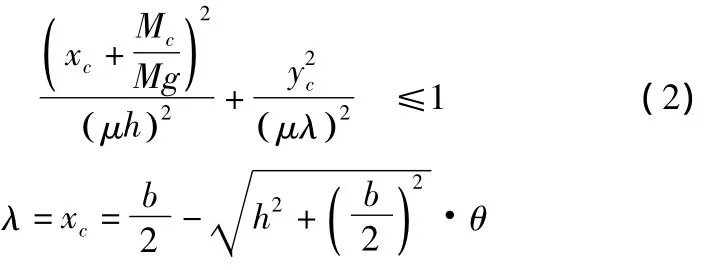
其中：M為康復器械系統的質量，MC為地面支撐足底各墊塊上作用的摩擦力等價到質心C點繞矢狀軸的力偶矩，h即單腳前進過程中，假設質心高度為常值;xc，yc分別為質心C的坐標，θ為康復器械的擺動角。

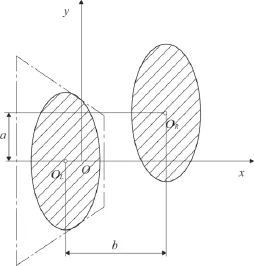
圖4 穩定域示意圖

圖中點畫線區域為腳部支撐域的范圍。由圖可知，系統質心在y軸方向的投影，邊界條件是不能超過橢圓的長半軸。

設系統的質心在y軸方向移動距離為a，則有：

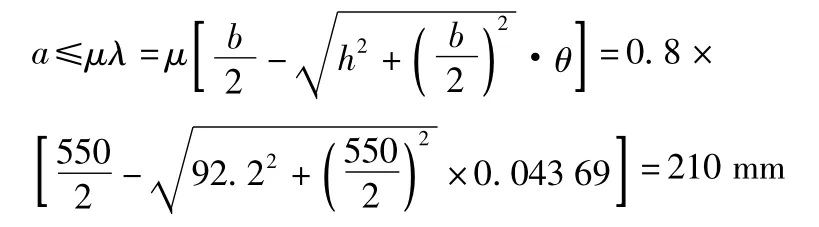
其中通過查閱中國青年人人體基本物理參數［7］，設定質心高度h為92.2 mm;θ為微幅左右擺動角，取弧度角為0.043 69;摩擦系數 μ 取0.8。

根據上述分析可知，系統質心的地面投影至穩定域的最小距離可作為判斷步行穩定程度的定量指標。

見大家交頭接耳竊竊私語，梅宏圖又開了腔：各位媒體的同行們，我有必要向大家匯報一下我的工作簡歷。鄙人大學讀的新聞系，畢業后，就進入老家的一家晚報，從通聯干起，記者、編輯、記者部主任、副主編、主編一路干下來，后來，經不起經濟大潮的誘惑，就下海弄潮了。

4 步行康復器械的仿真與分析

在ADAMS中，以樣條曲線擬合后作為樣條驅動函數來驅動步行康復器械按照規劃過的軌跡運動。通過腳本仿真在ADAMS后處理器里進行康復器械腰部和腳部運動速度和加速度分析，評估患者通過控制身體擺動控制康復器械避開障礙物的能力。同時，分別編輯系統質心在x軸和y軸方向運動函數，將其在仿真過程中的運動曲線和前面的理論分析進行比較參照，分析康復器械的運動穩定性。

4.1 步行康復器械步行穩定性試驗

在理論上建立康復器械穩定步行邊界條件的基礎上，通過ADAMS仿真，來分析穩定步行的可行性。

首先必須確定模型在仿真過程中整個系統質心的軌跡。根據多剛體系統動力學中多剛體運動質心的求法，來間接獲得整個系統質心的運動軌跡，即根據每個構件的質量和質心坐標來求出整個系統的質心方程：

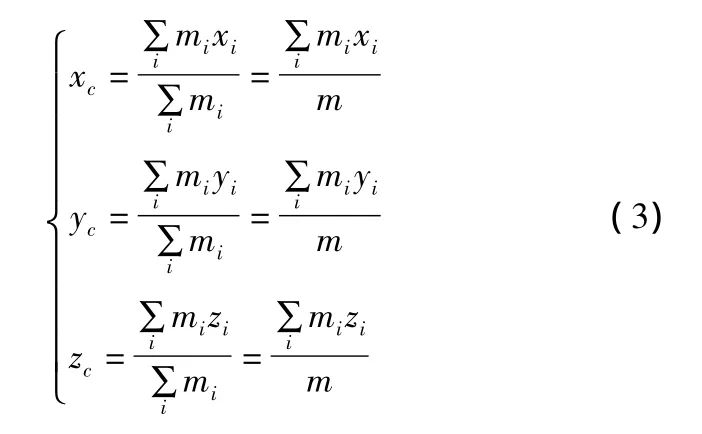
式中：mi表示第i個質點的質量，m表示質點系總質量，(xc，yc，zc)和(xi，yi，zi)分別為質點系和第i個質點的坐標。

應用ADAMS的函數編輯功能，分別編寫整個系統的質心相對于全局坐標系的軌跡方程。

通過仿真，得到整個系統的質心在全局坐標系下沿x軸和y軸方向的變化曲線，圖5為系統質心在x軸方向的位置曲線。

圖中實線表示整個系統質心在仿真過程中沿x軸方向的位置曲線，點劃線表示腳部延長機構墊塊在仿真過程中沿x軸方向的位置曲線，虛線表示腳部墊塊在仿真過程沿x軸方向的位置曲線。

圖5 系統質心在x軸方向的位置曲線

系統質心實曲線的水平段表示康復器械已經完全完成擺動，處于單腳支撐階段時，系統相對于全局坐標系的位置。點劃線表示腳部延長機構墊塊在仿真過程中相對于全局坐標系的位置。根據曲線可知，腳部支撐面積有足夠的安全裕度使整個系統保持穩定。

圖6為系統質心在y軸方向的位置曲線.

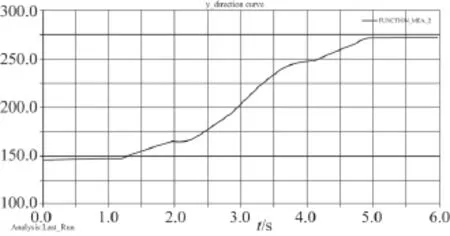
圖6 系統質心在y軸方向的位置曲線

從圖中曲線看出，系統質心在全局坐標系y軸方向的移動距離，即沿康復器械步行前進方向的距離約為125 mm。

根據前面所求單腳支撐階段的穩定域，比較步行穩定性的指標，可以確定步行康復器械的步行是穩定的。

4.2 避開障礙物的仿真試驗

利用患者健全的雙臂操縱轉向機構，改變康復器械步行方向。此外，還可以利用患者身體的擺動方向來控制系統在x軸方向的移動距離。

在第一個周期的步行過程中，康復器械會向初始擺動的方向移動一個δ距離即向x軸的負方向移動一個δ，y軸正方向為前進方向，如圖7。

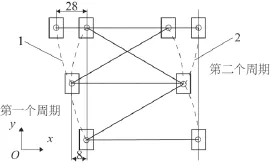
圖7 兩種不同的腳部落地方案

方案一：當患者完成第一個步行周期后，繼續向著x軸的負方向擺動一個δ距離(路線1)，則在完成第二個步行周期后，康復器械會向x軸的負方向移動兩個δ距離。方案二：當患者完成第一個步行周期后，卻沿著x軸的正方向擺動一個δ距離 (路線2)，則在完成第二個步行周期后，康復器械在x軸方向回到原來的位置坐標。圖中可知兩種方案在y軸正方向移動的距離相同。

分別針對這兩種步行模式進行了仿真分析，得到了左腳在仿真過程中在x軸方向的位置曲線，如圖8。

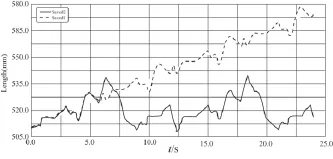
圖8 左腳在x軸方向的位移變化曲線

虛線的起止點坐標分別為(0，510.5)和(24，575)，可知康復器械在x軸方向移動了65.5 mm，再加上患者雙臂的作用，則康復器械具有一定避開前方障礙物的能力。

4.3 康復器械腰部的速度、加速度試驗

康復器械的腰部構件質心的速度和加速度沿y軸方向(步行方向)曲線如圖9，其中實線為速度曲線，虛線為加速度曲線。

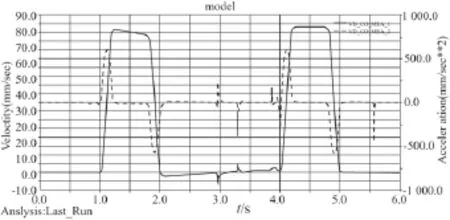
圖9 腰部重心的速度和加速度曲線圖

從速度曲線可以看出，腰部構件重心在1 s～2 s和4 s～5 s分別有一個加速、勻速和減速的過程，而且通過加速度曲線可知其加速度最大值為600 mm/s2左右，這表明步行康復器械在行走過程中，運行是平穩的。

而在3 s附近有兩次加速度突變是由于患者在擺正身體時，擺動腳在落地時振動引起的。由上述曲線圖可以看出，該情況對平穩步行的影響不是很大。

4.4 康復器械擺動腿的速度、加速度試驗

康復器械的腳部構件質心的速度和加速度沿y軸(步行前進方向)的曲線如圖10，其中實線為速度曲線，虛線為加速度曲線。

圖10 腳部重心的速度和加速度曲線圖

由速度曲線可知，腳部在步行過程中除了有一個勻速步行的時間段，還有一個加速和減速的過程，且擺動的加速度不是很大，運動穩定。

因此，由上述分析可知，仿真參數的設置是合理可行的，基本符合正常人的步行運動習慣。

5 結語

利用Pro/E和ADAMS對步行康復器械進行聯合運動仿真分析是一種可行、實用的方法。依據零力矩點(ZMP)理論，通過對康復器械的步行穩定性的分析，得出了其安全穩定區域，并為后續仿真分析做好基礎。通過ADAMS仿真可知，所設計的步行康復器械能夠實現一些基本的行走避障功能，并且步行穩定性較好。

［1］張慧.腦血管病癱瘓患者早期康復護理的實施［C］.中國康復醫學會第十屆全國腦血管病康復學術會議論文集，2007，107～109.

［2］方璐，劉小芳.心理關注在截癱患者康復期中的作用［J］.吉林醫學，2012，9(22)：1995.

［3］陳立平，張云清.機械系統動力學分析及ADAMS應用教程.［M］.北京：清華大學出版社，2006.

［4］杜中華，薛德慶，趙迎紅.Pro/E與ADAMS傳遞過程中若干問題的討論［J］.機械與電子，2003，2：68 ～70.

［5］Napoleon，Shigeki Nakaura.Balance Control Analysis of Humanoid Robot based on ZMP Feedback Control［J］.Proceedings of the IEEE/RSJ Int.Conf.on Intelligent Robots and Systems.2002：2437～2442.

［6］吳立勤，吳家麒，柯顯信.兩足機器人步行運動參數對單足支撐期ZMP點影響的研究［J］.光學精密工程，2000，9(6)：548～552.

［7］鄭秀瑗，賈書惠.現代運動生物力學［M］.北京：國防工業出版社，1998.