乏信息多傳感器壓力數據自助模糊融合估計

王中宇 王 倩

(北京航空航天大學 儀器科學與光電工程學院，北京100191)

付繼華

(中國地震局地殼應力研究所，北京100085)

乏信息[1]是指測量數據具有的測量信息不完整和不充足.例如概率分布已知，但僅有幾個數據用于數據處理;概率分布未知，測量數據也只有少量;趨勢項未知等都可認為其具有乏信息特征.隨著國防工業的發展，在航空、航天運載系統、載人航天工程系統、戰術導彈、飛行姿態控制、遙感測量、武器裝備及船舶制造等行業[2－4]壓力傳感器的使用比例較大.在這些領域的多傳感器壓力測量過程中，常出現測量次數較少，或者測量數據個數較少無法確定其概率分布等情況，因此乏信息特征存在于多傳感器壓力測量數據的融合估計過程中.

多傳感器數據融合是一個具有不確定特征的復雜數據處理過程，融合方法作為研究的熱點，一直受到人們的重視，這方面國內外已經作了大量的研究，并提出了許多融合方法[5].目前，這些方法大致可以分為兩類:概率統計方法[6]和人工智能方法[7].概率統計方法發展相對成熟和系統化，其中卡爾曼方法[8]廣泛應用于高斯分布的測量數據處理，貝葉斯估計[9]在分布未知的測量數據融合中具有優越性.人工智能又可分為邏輯推理方法和學習方法，邏輯推理屬于不確定性推理，對信息的表示和處理更加接近人類的思維方式，但是對信息的描述存在很大的主觀因素，對信息的表示和處理缺乏客觀性;學習方法目前包括神經網絡，映射學習方法，數據挖掘等[10－12]，學習方法自身理論方面還不夠完善，存在穩定性問題、泛化能力、缺乏有效的學習機制等.

以上所提研究方法從不同方面實現了多傳感器數據的融合，在很大程度上豐富和發展了多傳感器數據融合理論.人工智能方法與基于大數定律與中心極限定理的統計學方法，在測量數據概率分布未知或測量數據個數較少的乏信息條件下具有一定的局限性.近年來，自助法[13]，模糊數學理論[14]，灰色系統理論[15]等方法在處理乏信息問題上有一定應用.如文獻[14]中應用模糊數學理論實現了乏信息測量參數的有效估計;文獻[16]成功將自助法應用到多傳感器滑坡時間序列融合;文獻[15]運用灰自助法實現了乏信息虛擬儀器測量不確定度的評定.但這些方法在多傳感器壓力測量數據融合估計問題中尚未應用.

本文通過自助法對測量數據進行重復抽樣，增加測量數據的樣本量，進行多傳感器壓力測量數據融合，并利用模糊隸屬函數實現了壓力測量數據真值與區間估計.

1 自助模糊數據融合估計原理

自助模糊數據融合估計方法是將自助法[16]與模糊隸屬函數[14]的概念有機地結合起來，進行數據分析的一種本征融合方法.圖1為原理圖.

1.1 多傳感器壓力測量數據自助融合

在多傳感器壓力測量過程中，設小樣本空間的s個壓力傳感器獲得的測量數據時間序列為初始序列Z為

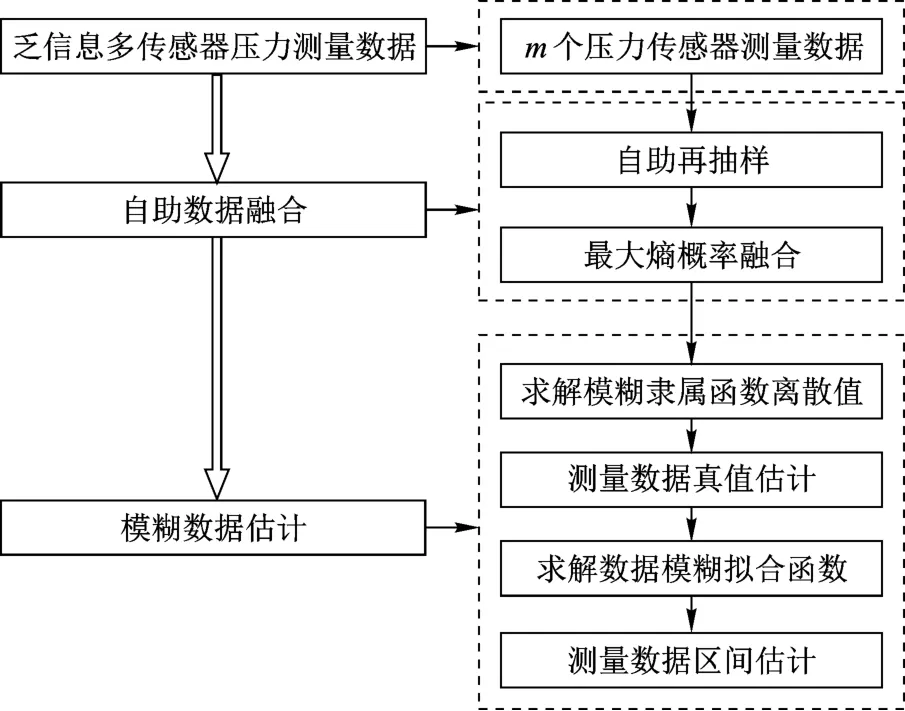
圖1 乏信息自助模糊融合估計原理

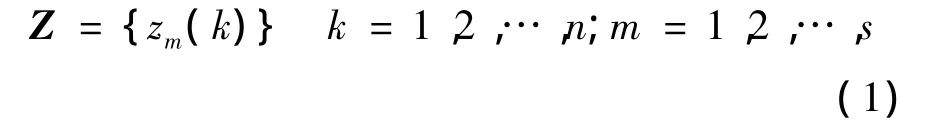
式中，zm(k)為第m個壓力傳感器獲得的第k個數據;k為時間;n為數據量.

在時間k，s個壓力傳感器測量數據為

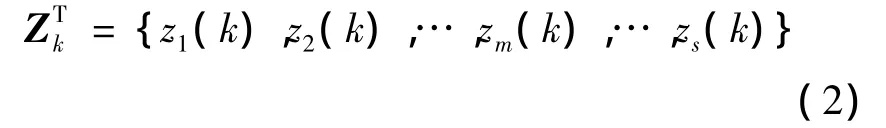
依據自助抽樣原理[15]，在中自助抽樣，獲得B個自助仿真樣本:

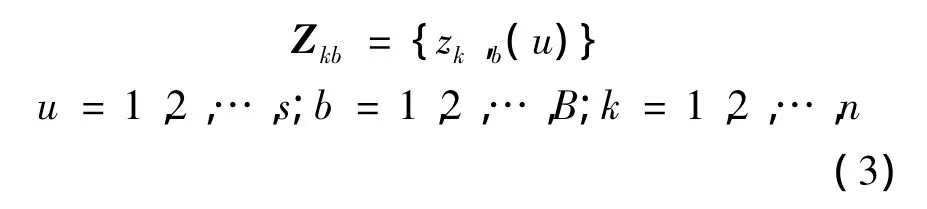
式中，zk，b(u)為時間k的第b個自助樣本中的第u個數據.

Zkb中每列的均值為

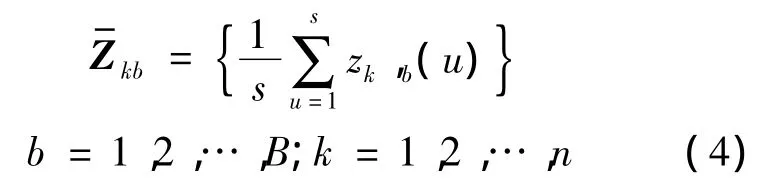
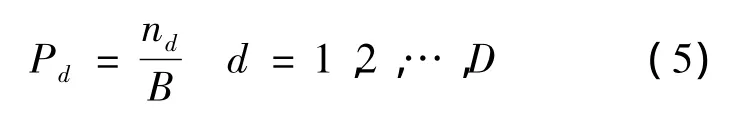
式中，nd為第d組的數據量.

將式(2)中離散值zm(k)替換為連續變量x，依據最大熵算法[15]，得自助分布概率密度函數p(x).

在時間k，s個壓力傳感器測量數據融合值用數學期望表示為

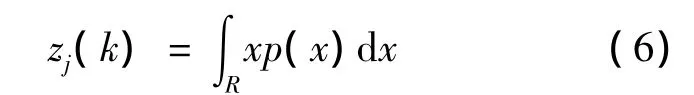
式中，R為積分空間.

式(6)可以用離散形式表示為加權均值:

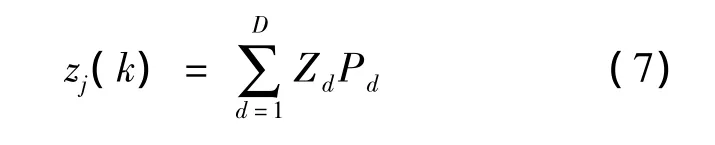
式中，Zd為第d組的組中值.

對于s個壓力傳感器測量數據，zj(k)構成一個時間融合序列，即自助融合序列Zj，用矩陣表示為

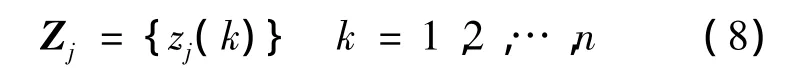
1.2 多傳感器壓力測量數據模糊估計

在模糊數學中，將離散數x(k)看作模糊數，連續的x即為模糊變量.

如圖2所示，x的隸屬函數定義:

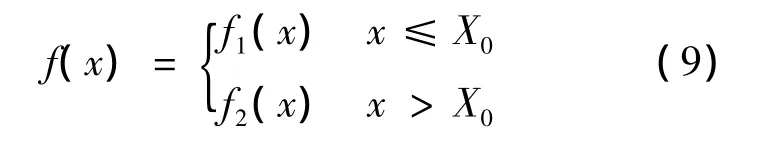
式中，f(x)∈[0，1]為隸屬函數;f1(x)為左增函數;f2(x)為右減函數;X0為測量參數總體分布的估計真值;[XL，XU]為在最優水平λ下的估計區間;XL為區間下限;XU為區間上限.

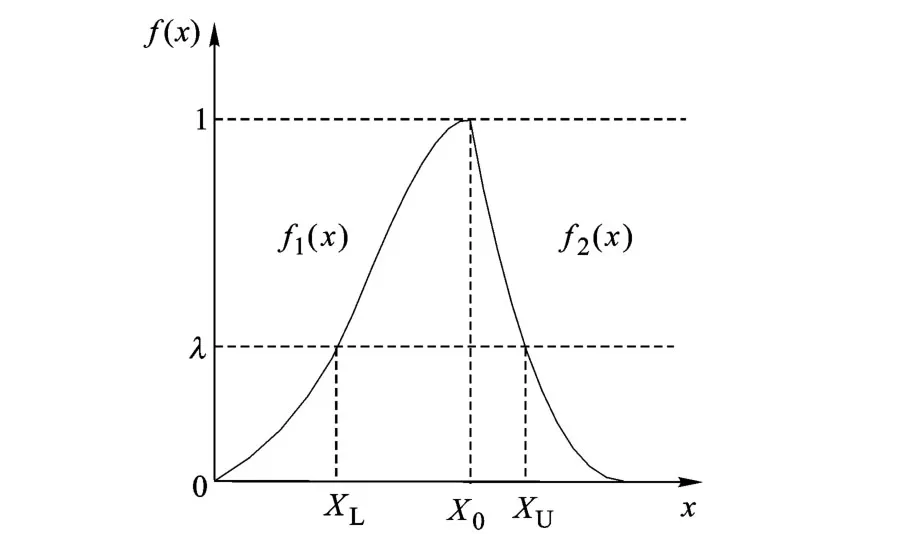
圖2 模糊隸屬函數圖

將Zj序列按升序排序，形成新序列Y={y(1)，y(2)，…，y(n)}.定義:

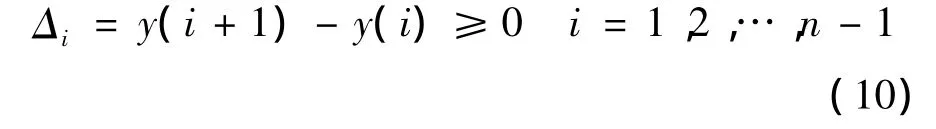
設線性隸屬函數:

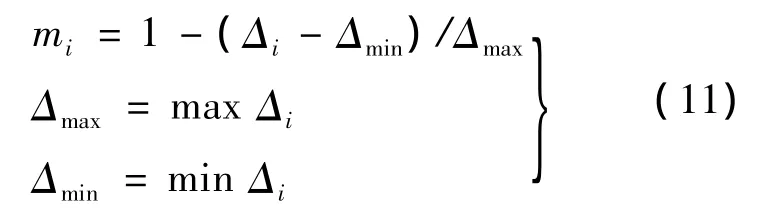
式中，i=1，2，…，n－1.

則滿足區間[0，1]的測量數據模糊隸屬離散值為

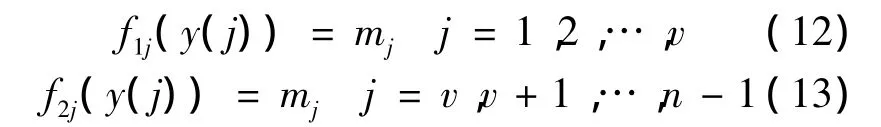
取最大mi對應的y(i)為真值X0的估計真值Xv，對應的序號i為v.

用下面兩個多項式擬合模糊隸屬函數:

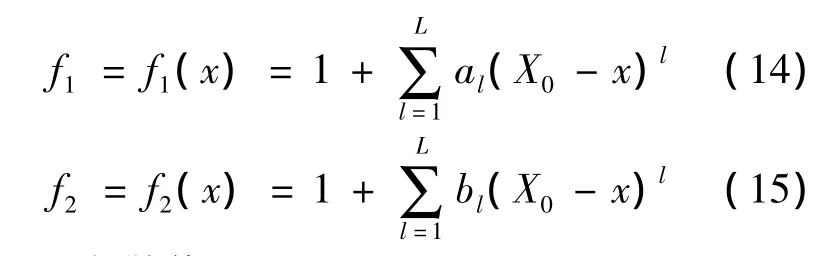
分別逼近離散值f1j(y(j))和f2j(y(j)).設

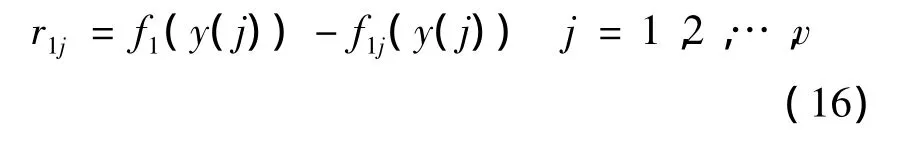
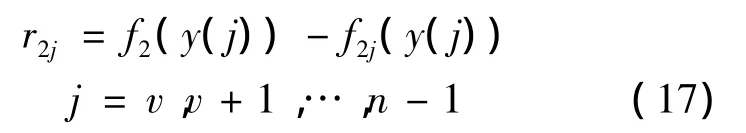
根據模糊集合理論意義上的最優水平λ，在模糊集合理論意義上，取λ= 0.5(λ∈[0，1]).確定相應的水平截集，得到乏信息多傳感器壓力測量數據的估計隸屬區間.可由下面兩式得XL和XU:

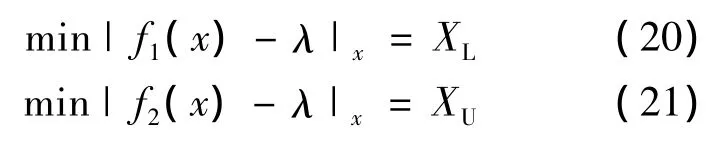
2 實例分析

為了說明算法的有效性，本文分別在乏信息和大樣本兩個條件下進行實驗驗證.

2.1 乏信息實驗分析

選取某壓力測量系統的4個檢測點壓力傳感器獲得的壓力值的時間序列數據Y1～Y4見表1.分別利用本文提出的自助模糊算法、多模型跟蹤法[17]以及均值融合法，進行乏信息多傳感器壓力測量數據融合估計.在本次實驗中，取m=4，n=11，Y={Y1，Y2，Y3，Y4}，B=1000.自助模糊法，多模型跟蹤法和均值融合法的融合序列如表2中F1，F2，F3所示.根據模糊隸屬函數得估計真值X0與區間[XL，XU]，見表2.

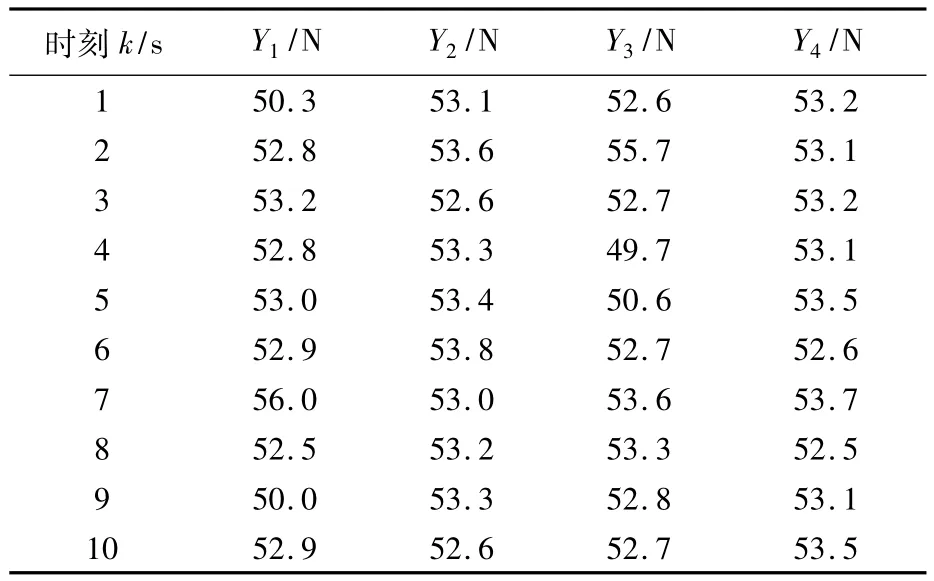
表1 乏信息多傳感器壓力測量數據原始時間序列

在本實驗中，進行數據融合對比分析，據表2，F1和F2的數據接近，均能綜合反映該測量過程的演化情況.圖3描述了原始測量數據序列與自助融合序列.由圖3可得，本文算法所得融合序列與原始測量數據的變化趨勢接近，能夠精確地描述和反映測量系統的狀態.為了對算法的性能分析，本文利用區間分析對測量數據進行了檢驗，區間估計精度如圖4所示.由圖4可得，自助模糊模型區間判定的精度為87%，其次多模型跟蹤法為82%，均值融合僅能達到57%.由此數據可以看出，在乏信息條件下，自助模糊模型能夠有效地實現多傳感器測量數據融合，融合過程中對測量數據個數及其分布規律都沒有要求.

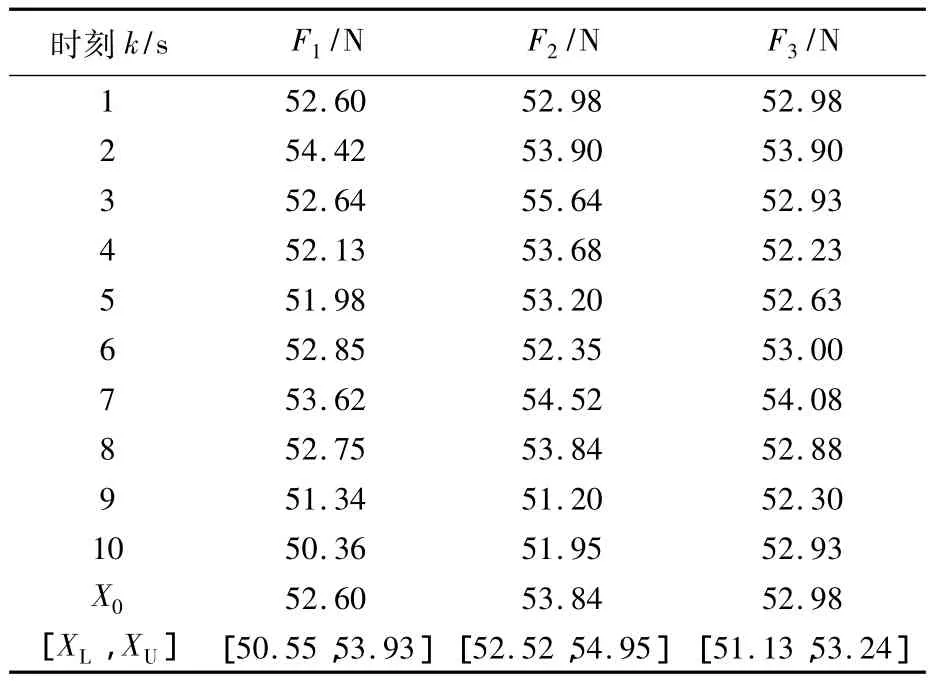
表2 乏信息多傳感器壓力測量數據融合序列

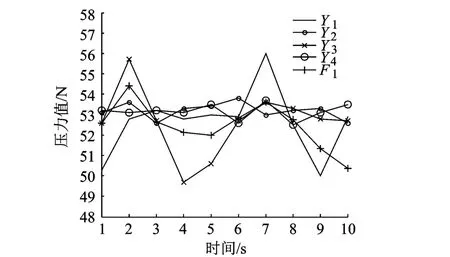
圖3 融合對比圖

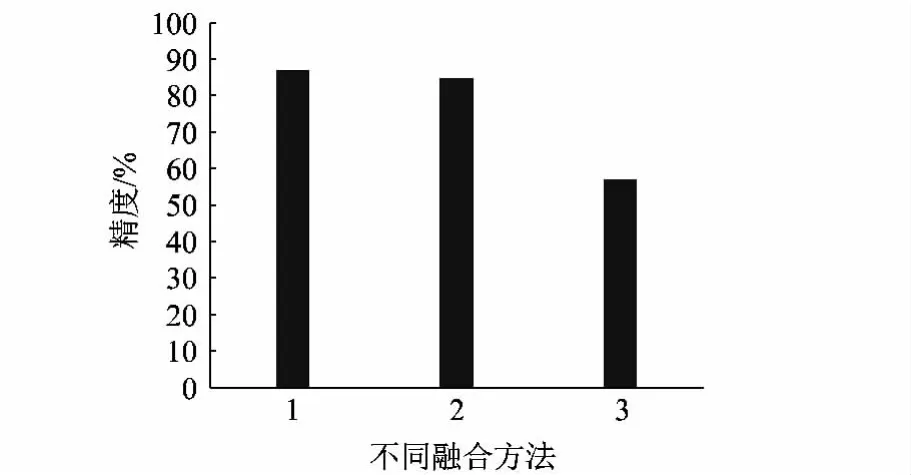
圖4 區間估計精度圖

2.2 大樣本仿真實驗分析

在大樣本量的情況下，為考核融合估計效果，定義置信水平P下的波動范圍為

定義對波動范圍真值U0估計的相對誤差(絕對值)為

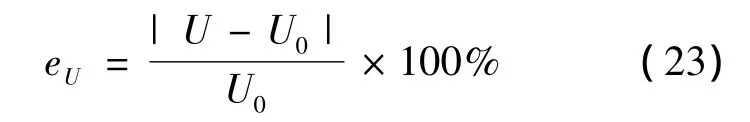
在置信水平P下，誤報率PE為

式中，e為位于估計區間U外數據;n為乏信息子樣本數據總數.

可靠度Pr為

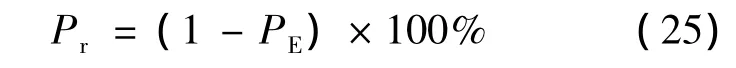
本文選取正態分布的測量數據進行仿真實驗，設定特征參數為標準差σ=0.1和真值X0=52，仿真出N=1024個數據x(k).仿真出的1024個數據可以被認為是大樣本測量數據.用統計法進行估計，得到此組大樣本數據的σ=0.0977.取P=99.73%，得到波動范圍的約定真值U0=6σ=0.5862.

在此樣本數據序列中，抽取乏信息子樣本，從這1024個數據中抽4組數據，每組數據個數為n=10個，構成數據序列C1～C4，對這4組數據，應用自助模糊方法與統計方法進行融合估計，結果如表3所示.

由表3可知，在乏信息條件下，相較于統計方法，自助模糊方法的融合估計結果與約定真值差異較小.數據表明:自助模糊方法可以很好地實現具有乏信息特征的測量數據融合估計.自助模糊估計較大樣本約定真值的相對誤差為10%左右，接近于真實的測量數據，在P為99.7%下，區間估計的Pr可達95%，說明此方法可以較為準確地描述測量系統的特征參數，反映測量過程的真實情況.

表3 仿真實驗結果對比

3 結論

依據乏信息多傳感器壓力測量數據融合估計問題的特征，本文提出了乏信息多傳感器壓力測量數據自助模糊融合估計模型，拓展了融合估計方法的條件限制，并通過實際測量數據進行驗證.其中，自助抽樣對樣本量進行擴充，允許原始測量數據個數有限，而且對數據的概率分布無任何要求;模糊估計實現最少僅需3個數據而且同樣無需測量數據概率分布信息.實驗表明:在乏信息條件下，算法精度可達87%;在大樣本條件下，測量數據在置信水平99.7%下，融合估計可靠性可達95%，所以自助模糊融合估計模型，能利用少量的測量數據對具有乏信息特征的壓力傳感器測量數據的測量真值與區間進行有效估計，從而全面地掌握被測量的真實情況，最大限度的避免漏報、誤報.通過算例有效地驗證了自助模糊融合估計模型的可行性和科學性.

References)

[1]葛樂矣，趙偉，徐子帆，等.乏信息動態測量誤差灰自助預報[J].農業機械學報，2011，42(7):210－214，219

Ge Leyi，Zhao Wei，Xu Zifan，et al.Error predicting for dynamic measurement of poor information based on grey bootstrap method[J].Transactions of the Chinese Society for Agricultural Machinery，2011，42(7):210－214，219(in Chinese)

[2]Seiler F，Srulijes J.New results in numerical and experimental fluid mechanics IV[M].Germany:Springer-Verlag Berlin and Heidelberg GmbH＆co K，2004:87，124－131

[3]Kotomin A A，Shirokova N P，Dushenok S A，et al.Detonation pressure of explosive charges applied in spacecraft division systems[J].Solar System Research，2011，45(7):677－683

[4]Tao Zui，Qin Bangyong，Li Ziwei，et al.Satellite observations of the partial pressure of carbon dioxide in the surface water of the Huanghai sea and the Bohai sea[J].Acta Oceanologica Sinica，2012，31(3):67－73

[5]Khaleghi B，Khamis A，Karray F O，et al.Multisensor data fusion:a review of the state of the art[J].Information Fusion，2013，14(1):28－44

[6]Chen Yukun，Si Xicai，Li Zhigang.Research on Kalman-filter based multisensor data fusion[J].Journal of Systems Engineering and Electronics，2007，18(3):497－502

[7]Noureldin A，El-Shafie A，Taha M R.Optimizing neuro-fuzzy modules for data fusion of vehicular navigation systems using temporal cross-validation[J].Engineering Applications of Artificial Intelligence，2007，20(1):49－61

[8]Deng Zili，Zhang Peng，Qi Wenjuan，et al.Sequential covariance intersection fusion Kalman filter[J].Information Sciences，2012，189:293－309

[9]Zhu Hao，Henry Leung，He Zhongshi.A variational Bayesian approach to robust sensor fusion based on Student-t distribution[J].Information Sciences，2013，221:201－214

[10]Caron F，Davy M，Duflos E，et al.Particle filtering for multisensor data fusion with switching observation models:Application to land vehicle positioning[J].IEEE Transactions on Signal Processing，2007，55(6Part 1):2703－2719

[11]Noureldin A，Osman A，El-Sheimy N.A neuro-wavelet method for multi-sensor system integration for vehicular navigation[J].Measurement Science＆Technology，2004，15(2):404－412

[12]Vega J，Pereira A，Portas A，et al.Data mining technique for fast retrieval of similar waveforms in Fusion massive databases[J].Fusion Engineering and Design，2008，83(1):132－139

[13]Xia Xintao，Chen Xiaoyang，Zhang Yongzhen，et al.Grey bootstrap method of evaluation of uncertainty in dynamic measurement[J].Measurement，2008，41(6):687－696

[14]Wang Qian，Fu Jihua，Wang Zhongyu，et al.A seismic intensity estimation method based on the fuzzy-norm theory[J].Soil Dynamics and Earthquake Engineering，2012，40:109－117

[15]Ge Leyi，Wang Zhongyu.Novel uncertainty-evaluation method of virtual instrument small sample size[J].Journal of Testing and Evaluation，2008，36(3):273－279

[16]夏新濤，陳曉陽，張永振，等.多傳感器滑坡時間序列的自助融合及其灰假設檢驗[J].巖土力學與工程學報，2007，26(9):1904－1912

Xia Xintao，Chen Xiaoyang，Zhang Yongzhen，et al.Bootstrap fusion and its grey hypothesis testing for landslide time series of multi-sensor[J].Chinese Journal of Rock Mechanics and Engineering，2007，26(9):1904－1912(in Chinese)

[17]郭科，彭繼兵，許強，等.滑坡多點數據融合中的多傳感器目標跟蹤技術應用[J].巖土力學，2006，27(3):479－481

Guo Ke，Peng Jibing，Xu Qiang，et al.Application of multi-sensor target tracking to multi-station monitoring data fusion in landslide[J].Rock and Soil Mechanics，2006，27(3):479－481(in Chinese)