GPS中頻信號和IMU信號模擬及驗證

王可東 胡 正 侯紹東

(北京航空航天大學 宇航學院，北京100191)

由于GPS與慣性導航系統(INS，Inertial Navigation System)之間有很強的互補性，二者的組合在提高導航精度的同時，極大地提高了導航系統的可靠性[1].按照組合信息的利用程度，組合系統又分為松組合、緊組合和超緊組合或深組合[2－5]，松組合和緊組合研究成果已經在實際中得到了應用，目前的研究重點是超緊組合.在研究組合導航的過程中，為了驗證組合方案和算法的性能，有必要進行仿真和/或實際實驗，由于實際實驗場景構建復雜、成本高和不方便[5]，在研究過程中往往更多是依賴仿真實驗.但是，商用信號模擬器主要存在如下問題:①成本高[6－7].Spirent這類模擬器都百萬元計，國內的也是要30萬元左右1個頻點;②功能有限[6－9].目前的模擬器只有衛星信號模擬功能，IMU(Inertial Measurement U-nit)信號模擬不開放，國內的模擬器很多沒有IMU模擬功能，導致對組合系統驗證不了;③干擾模擬不足[10].干擾分欺騙式和壓制式，而一般的干擾信號模擬需要單獨的干擾機來實現，而且幾乎都是壓制式干擾模擬.

本文針對目前組合導航研究中的驗證需求和模擬器的上述不足，以GPS/INS組合導航方案和算法研究為應用對象，采用VC++語言進行GPS中頻信號和IMU信號的模擬，研究了中頻信號和IMU信號的仿真方法，并對典型的干擾進行了模擬.與現有的基于原理級信號模擬不同，本文采用的是信號級仿真，使得驗證的有效性大大增強，解算結果初步驗證了模擬信號以及干擾的有效性.

1 載體運動模型建模

載體運動模型采用運動學原理進行構建，定義了平飛、俯仰、橫滾和偏航等4種基本運動.

1.1 坐標系選取

載體的運動是在發射點地理坐標下定義的，其中發射點地理坐標系與地球固連，原點位于載體的初始位置，Z軸為地心與原點的連線指向地表外，X軸指向正東方向，Y軸指向正北方向.

1.2 載體運動定義

載體的運動模型主要通過式(1)～式(3)定義.

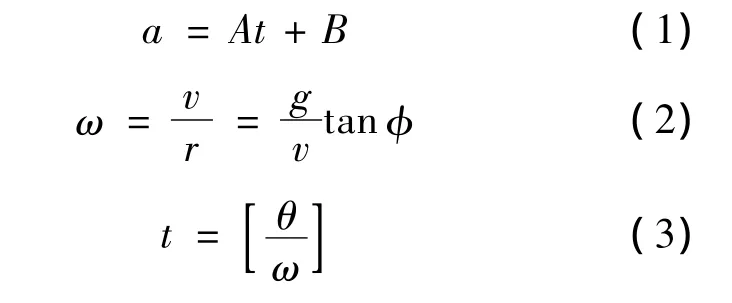
其中，a為運動加速度;t為運動時間;A和B為常數;θ和ω分別為姿態角和角速度;v為運動速度;r為圓周運動半徑;g為重力加速度;φ為橫滾角;[·]表示取整運算.

由式(1)可知，當A和B取不同值時可以產生勻加加速度、勻加速度和勻速等平飛運動.俯仰運動的角度和角速度是設定的已知參數，分別為θ和ω，由式(3)得到運動時間t.橫滾運動也遵循勻速圓周運動規律，橫滾角度和橫滾角速度分別為θ和ω，橫滾運動時間t按式(3)計算.偏航運動前，必須先進行橫滾運動，假設橫滾運動結束時，載體的運動速度是v，橫滾角度是φ，若載體偏航的角度設定為θ，那么偏航運動的角速度ω由式(2)來計算.式(2)成立的前提是偏航運動也遵循勻速圓周運動規律.偏航運動的運動時間t由式(3)得到.

2 GPS信號和IMU信號輸出

GPS中頻信號產生的方法比較簡單，關鍵是多普勒頻移的計算，模擬原理請參考文獻[11－12].下面主要介紹IMU信號的產生原理.

2.1 坐標系之間的關系

載體的所有運動都是在發射點地理坐標系下定義的，因此必須明確地心地固坐標系(簡稱e系)、發射點地理坐標系(簡稱c系)和載體坐標系(簡稱b系)三者之間的關系.載體坐標系與載體固連，原點與載體的質心重合，xb軸沿載體橫軸指右，yb軸沿著載體縱軸指前，zb沿著載體豎軸并與xb，yb構成右手直角坐標系[13].在載體運動的起始時刻，載體的起始位置作為發射點地理坐標系的原點.假設由e系轉換為b系的矩陣為，由e系轉換為c系的矩陣為，由c系轉換為b系的矩陣是，則矩陣之間的關系由式(4)表示為

2.2 初始四元數的計算

姿態轉移矩陣的更新是用四元數來實現的.假設初始時刻的四元數是F0，F0=[λ0λ1λ2λ3]T，載體初始位置的經度是λ，緯度是l，那么[14]:

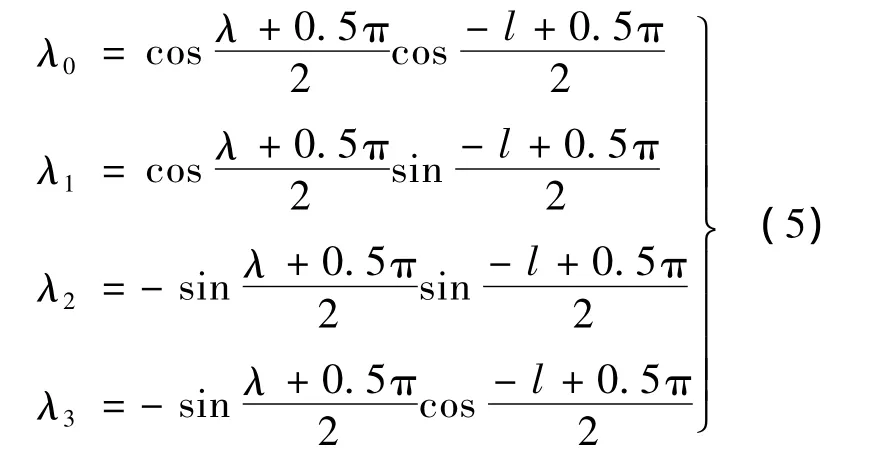
2.3 四元數、比力以及角速度更新

比力的計算可以參考文獻[13－14].角速度為

其中，ωi表示b系中角速度;表示載體相對于地球轉動的角速度;ωie表示地球自轉角速度.

設姿態四元數為 F =[y0y1y2y3]T，下面介紹不同運動中F的更新方法.

2.3.1 平飛運動

平飛過程中，四元數保持不變，無需更新.

2.3.2 俯仰運動

當載體繞著b系X軸做俯仰運動時，如果載體每毫秒轉過的角度是Δθ，則F的迭代為

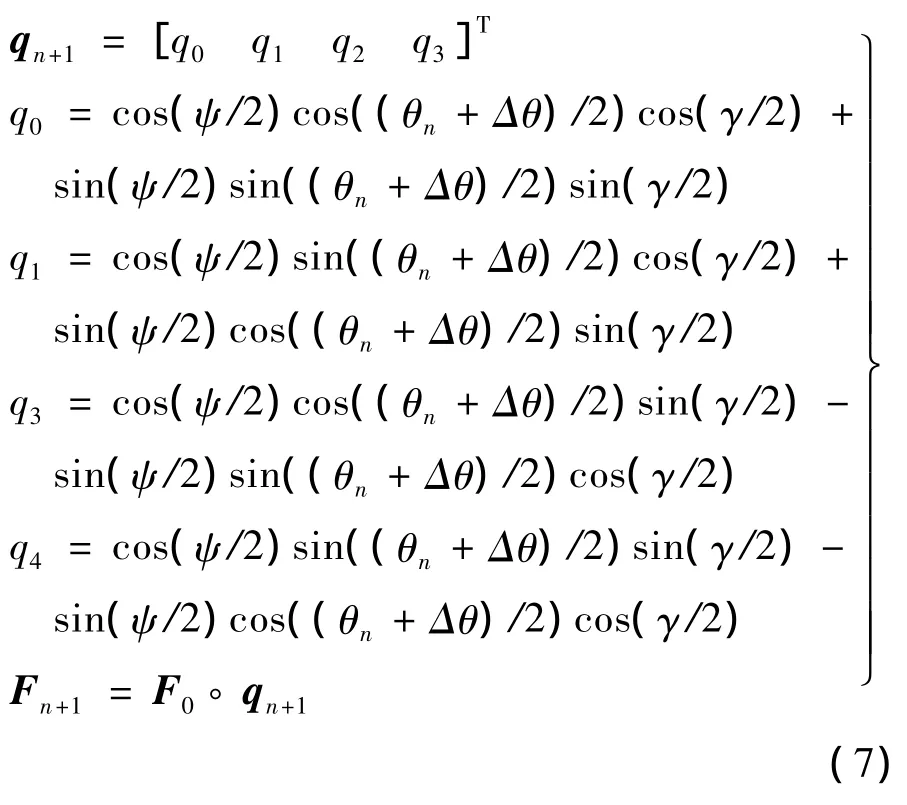
其中，四元數q為b系和c系之間轉動關系;ψ和γ為載體相對于c系的偏航角和橫滾角;F0為初始四元數值;?為四元數乘積運算.

2.3.3 橫滾運動

載體繞著b系Y軸做橫滾運動，四元數計算方法同俯仰運動的計算方法一樣，不再贅述.

2.3.4 偏航運動

偏航運動中，載體繞著c系的Z軸轉動，若每毫秒轉過的偏航角為Δψ，則F迭代為

其中Q表示載體繞c系Z軸轉過Δψ.

3 干擾環境模擬

轉發式干擾就是將干擾機接收到的GPS導航信號經過一定的延時放大后直接發送出去.轉發式干擾利用信號的自然延時，因此干擾信號與導航信號完全相同，只是延時不同，GPS接收機容易被欺騙.另外轉發式干擾信號經過放大，信號的幅度大于導航信息的幅度.GPS接收機完全有可能將轉發的干擾信號捕獲到，從而獲得錯誤的偽碼，使GPS接收機無法精確定位[15].

壓制式干擾是GPS接收機面臨的重要威脅之一，對偽碼跟蹤的跟蹤精度產生影響，甚至導致偽碼跟蹤環失鎖.模擬的壓制式干擾包括寬帶高斯噪聲干擾、窄帶干擾、連續波干擾和鋸齒調頻連續波干擾等[16].寬帶高斯噪聲干擾是高斯白噪聲，干擾頻帶覆蓋了衛星發射信號的全部頻帶;窄帶干擾是高斯白噪聲通過一個低通濾波器，得到滿足條件噪聲帶寬;連續波干擾是與GPS信號載波同頻的尖峰干擾，采用頻率瞄準技術，使干擾載頻精確對準GPS信號的載波頻率，針對特定碼型的衛星信號實施干擾，使信號在一定區域內失效;鋸齒調頻波是一種調頻連續波，調頻連續波是指頻率隨時間按調制信號規律變化的波形，鋸齒調頻波的頻率和相位表達式請參考文獻[17].

4 軟件仿真測試

仿真測試包括兩部分:①中頻信號和IMU信號仿真算法的驗證;②針對干擾環境的場景模擬，驗證添加干擾的有效性.

4.1 信號仿真算法驗證

4.1.1 軌跡發生

模擬器軌跡發生參數設定:①靜止段:載體在初始位置靜止30 s;②平飛段:加速度是1g，運動時間2 s;③俯仰段:以1(°)/s的角速度俯仰10°;④俯仰段:以－1(°)/s的角速度俯仰－10°;⑤橫滾段:以1(°)/s的速度橫滾5°;⑥偏航段:以a=g·tan(5π/180)的向心加速度偏航90°;⑦橫滾段:以1(°)/s的速度橫滾－5°;⑧橫滾段:以－1(°)/s的速度橫滾－5°;⑨偏航段:以a=－g·tan(5π/180)的向心加速度偏航－90°;⑩橫滾段:以1(°)/s的角速度橫滾5°.

中頻信號采樣頻率是5.714 MHz;中頻數據量化位數是2.陀螺和加速度計誤差引入了常值漂移、隨機漂移和一階馬爾科夫過程噪聲.加速度計的三軸常值漂移均為100 μg，三軸隨機漂移100μg，一階馬爾科夫過程的相關時間是0.5h，均方差是100 μg;陀螺的三軸常值漂移是0.01(°)/h，三軸隨機漂移是0.01(°)/h，一階馬爾科夫過程的相關時間是1 h，均方差是0.01(°)/h.

模擬器產生的載體運動軌跡如圖1所示.

圖1 載體運動軌跡圖

4.1.2 軟件接收機對中頻數據及IMU數據解算

使用組合導航軟件接收機深組合算法對模擬器輸出的中頻數據以及IMU數據進行解算，得到如圖2所示組合導航解算的位置誤差圖和如圖3所示組合導航解算的速度誤差圖.通過對位置誤差和速度誤差數據分析可知，誤差限制在一定的可接受范圍內.對誤差數據的分析證明了載體運動模型是有效的，中頻數據以及比力、角速度更新算法是正確的.

圖2 組合導航解算的位置誤差圖

圖3 組合導航解算的速度誤差圖

4.2 干擾環境模擬場景驗證

在信號接收過程中500～600 ms處添加鋸齒調頻波干擾，干信比為40 dB，在600 ms處進行重新捕獲、跟蹤.圖4是PRN19衛星的多普勒頻移，載波多普勒頻移在干擾消失后，經過一段時間后又恢復到穩定的跟蹤狀態.其他形式的干擾效果不再給出.

圖4 鋸齒調頻波干擾對多普勒頻移的影響

通過實驗可以發現，當對中頻信號添加干擾時，接收機鎖相環跟蹤的多普勒頻移發生劇烈變化，甚至失鎖.實驗結果表明模擬器中添加的干擾達到了預期的效果.

5 結論

文中通過載體運動模型的建立，分析了中頻數據、IMU數據以及四元數的仿真更新方法.同時，引入了干擾模型.通過組合導航軟件接收機對模擬器輸出的中頻信號、IMU信號進行計算，證明載體運動模型的正確以及中頻數據、比力、角速度、四元數仿真算法的正確.通過添加干擾，發現其對載波的多普勒頻移造成了較大的影響，使鎖相環的跟蹤性能下降甚至失鎖，證明了添加干擾的有效性.下一步目標是基于干擾模型的場景模擬，研究干擾環境下接收機的抗干擾算法.

References)

[1]Brenner M.Integrated GPS/inertial fault detection availability[J].Journal of the Institute of Navigation，1996，43(2):111－130

[2]Noureldin A，Karamat T B，Eberts M D，et al.Performance enhancement of MEMS-based INS/GPS integration for low-cost navigation applications[J].IEEE Transactions on Vehicle Technology，2009，58(3):1077－1096

[3]Knight D T.Rapid development of tightly coupled GPS/INS systems[J].IEEE Aerospace and Electronic Systems Magazine，1999，12(2):14－18

[4]Soloviev A，Gunawardena S，Graas F V.Deeply integrated GPS/low-cost IMU for low CNR signal processing:concept description and in-flight demonstration[J].Journal of the Institute of Navigation，2008，55(1):1－13

[5]Gebre E.What is the difference between‘loose’，‘tight’，‘ultra-tight’and‘deep’integration strategies for INS and GNSS[J].Inside GNSS，2007，2(1):28－33

[6]Fedora N，Ford C，Boulton P.A versatile solution for testing GPS/inertial navigation systems[C]//Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation.New York:Curran Associates Inc，2008:992－1001

[7]東方聯星公司.NS800多系統導航衛星信號模擬器[EB/OL].[2013-08-02].http://www.olinkstar.com/products/ls-0852812500633.aspx

OlinkStar Co.，Ltd.NS800 Multi-system navigation satellite signal simulator[EB/OL].[2013-08-02].http://www.olinkstar.com/products/ls-0852812500633.aspx(in Chinese)

[8]Dong L.IF GPS signal simulator development and verification[D].Alberta:Calgary University，2003

[9]侯博，謝杰，劉光斌.衛星信號模擬器的發展現狀與趨勢[J].電訊技術，2011，51(5):127－132

Hou Bo，Xie Jie，Liu Guangbin.Navigation satellite signal simulator:current states and developing trend[J].Telecommunication Engineering，2011，51(5):127－132(in Chinese)

[10]鄭曉冬.衛星導航系統復雜干擾信號模擬源設計[D].成都:電子科技大學，2012

Zheng Xiaodong.The design for complex interference signal simulator of satellite navigation systems[D].Chengdu:University of Electronic Science and Technology of China，2012(in Chinese)

[11]謝鋼.GPS原理與接收機設計[M].北京:電子工業出版社，2009:74－75

Xie Gang.Principles of GPS and receiver design[M].Beijing:Publishing House of Electronics Industry，2009:74－75(in Chinese)

[12]趙軍詳，張其善，常青，等.高動態GPS衛星信號模擬器關鍵技術分析及應用[J].電訊技術，2003，46(4)，49－54

Zhao Junxiang，Zhang Qishan，Chang Qing，et al.The key technique analysis and applications of high dynamic GPS signal simulato[J].Telecommunication Engineering，2003，46(4)，49－54(in Chinese)

[13]于波，陳云相，郭秀中.慣性技術[M].北京:北京理工大學出版社，1994:13－14

Yu Bo，Chen Yunxiang，Guo Xiuzhong.Inertial technology[M].Beijing:Beijing Institute of Technology Press，1994:13－14(in Chinese)

[14]以光衢.慣性導航原理[M].北京:航空工業出版社，1987:84－85

Yi Guangqu.Inertial navigation principle[M].Beijing:Aviation Industry Press，1987:84－85(in Chinese)

[15]解晶，劉暢.轉發式GPS干擾技術及其仿真[J].儀器儀表用戶，2011，18(5):71－73

Xie Jing，Liu Chang.GPS repeater-jamming and performances simulation[J].Instrumentation Customer，2011，18(5):71－73(in Chinese)

[16]Chang Chungliang，Juang Jyh Ching.Performance analysis of narrowband interference mitigation and near-far resistance scheme for GNSS receivers[J].Signal Processing，2010(90):2676－2685

[17]郭偉榮，粟蘋，陳慧敏，等.鋸齒調頻連續波建模與數值仿真[J].紅外與激光工程，2009，38(6):977－980

Guo Weirong，Su Ping，Chen Huimin，et al.Modeling and numerical simulation of sawtooth FMCW[J].Infrared and Laser Engineering，2009，38(6):977－980(in Chinese)