基于方差的保障時間不確定性分析

吳 勇 潘 星 康 銳 馬 麟

(北京航空航天大學 可靠性與系統工程學院，北京100191)

裝備的保障過程是一系列不同類型的具有不同邏輯關系的保障活動的集合.對保障過程進行分析是對保障系統進行評價的基礎.保障系統有眾多評價指標，其中及時性指標是對保障時間進行評價的重要指標[1].由于保障活動受到資源、時間、工作環境以及人為操作等許多不確定因素的影響，使得保障過程工期(保障時間)呈現出不確定的性質.對于保障時間來說，保障過程模型輸入的不確定性導致了模型輸出的不確定性[2].保障時間的不確定分析可以通過對保障過程工期模型的敏感性分析，辨識那些對保障時間不確定性影響最大的保障活動，通過對不確定性影響最大的保障活動進行控制以實現對保障過程工期的精確控制，為保障決策提供定量支持.

為了對保障時間進行分析，首先需要對保障過程工期進行建模.目前針對保障過程工期建模的方法主要有cPM/PERT方法、GERT方法、IDEF3方法和Petri網等[3].由于PERT方法不允許回路存在，也就意味著無法對某一保障活動的重復執行進行描述，Petri網和IDEF3方法對模型無法進行有效解析，因此基于GERT方法對保障過程得到了較為廣泛的應用.GERT方法可以從活動邏輯關系分析入手，建立保障過程的隨機網絡圖，允許保障活動的重復執行，考慮活動及各個進度路徑的選擇和廢棄，較好地描述了保障過程中保障活動之間的邏輯關系.文獻[3]利用GERT方法建立維修活動的隨機網絡模型，并利用其解析算法對維修時間進行了精確計算;文獻[4]通過概率計算和蒙特卡洛仿真的手段對各活動歷時進行估計，在此基礎上，利用GERT方法對搶修工時進行計算.

保障時間的不確定性受到眾多保障活動參數的影響，對保障時間不確定性分析目的是要找到對其不確定性影響最大的保障活動.不確定分析是通過模型敏感性分析(SA，Sensitivity Analysis)辨識出那些輸入的不確定性參數對整個模型輸出的不確定性影響最大，是近來在風險研究中一個重要而受到廣泛關注的問題[5].不確定性分析方法可分為以下三類:文獻[6]提出的局部敏感性分析(local sensitivity analysis);文獻[7]提出的篩查方法(screening methods);文獻[8]提出的全局敏感性分析(global sensitivity analysis)，也稱為全局分析.其中，局部敏感性分析只能用在不確定因素單一的情況，篩查方法由于計算成本太高而只適應于輸入參數數量龐大的情況[7]，這兩種方法顯然不適用于保障過程的不確定性分析.全局敏感性分析[9－12]是目前應用最為廣泛的方法.Saltelli在文獻[8]提出了這種全局分析的基本原則，在此基礎上，在文獻[9]中提出了基于方差的全局性敏感性分析方法，并證明了該方法的有效性.

為了對保障過程的不確定性進行分析，本文建立了保障活動的不確定性重要度模型，在此基礎上，選用GERT(Graphic Evaluation and Review Technique)方法對保障時間進行建模，并設計了一種基于方差的保障時間不確定性分析方法來求解保障活動的時間不確定性重要度指標.最后，結合航母艦載機的具體案例來驗證了方法對分析保障活動不確定影響的有效性.

1 保障過程不確定性分析

1.1 保障任務與保障活動

在裝備保障過程中，存在著多種保障任務，其對應的保障活動也不一樣.通常來講，裝備的保障任務和其包含的主要的保障活動如下.

1)使用保障.主要指為保證裝備正確動用以便能充分發揮規定的作戰能力所進行的一系列技術和管理活動，例如使用前檢查、加注燃料和彈藥、動用人員及人力準備及裝備儲存與運輸等.

2)維修保障.主要指為保持和恢復裝備完成的技術狀況所進行的保障工作，如裝備的預防性維修與修復性維修、戰場搶修等.

3)供應保障.主要指為裝備提供相應的器材供應所進行的保障工作，如備件供應、彈藥供應、燃油供應、氣體供應和耗材供應等.

4)訓練保障.主要指為完成裝備訓練任務而采取的各種保障措施，如使用人員訓練、保障人員訓練、教員訓練和管理人員訓練等.

以上保障任務中各保障活動會根據裝備類型不同而不同，如可按專業將設備劃分為電子類、機械類，裝備的維修保障工作是其不同工作項目的任務組合.保障類型和保障活動的多樣性導致保障過程的不確定性尤為突出，通過不確定分析建模辨識不同保障活動的重要度，為保障資源配置提供支持.

1.2 保障活動不確定性重要度

正是由于裝備保障活動的多樣性，它們的保障內容和時間千差萬別，當某一保障活動的參數(時間、頻率等)發生波動時，就會對整個裝備保障過程產生重要影響.從時間參數角度來講，保障活動的執行時間對整個裝備保障時間的影響即稱為保障活動時間不確定性.

如用模型表示不確定環境下的保障過程:

其中，Y表示保障過程的輸出;X=X1，X2，…，Xk表示K個獨立的輸入，即互相獨立的保障活動參數.函數f(X)為平方可積函數，則根據方差分析的相關定義，可以得到:

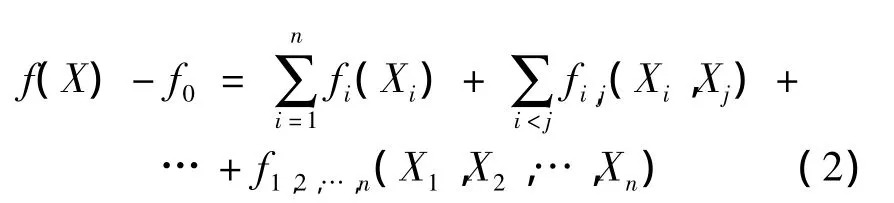
因此，由式(2)變形可以得到函數輸出Y的方差V[Y]的分解式為

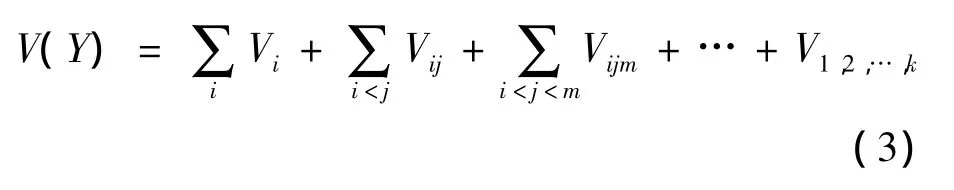
其中，Vi與Vij分別為輸入函數滿足一定條件時Y的期望的方差，即

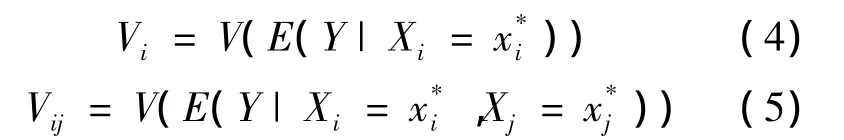
根據條件方差公式[13]可得

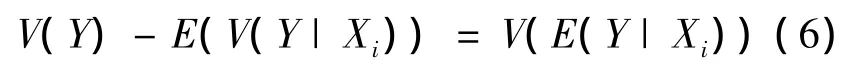
當感興趣的保障活動的輸入參數Xi已知時，保障活動不確定重要度全局性評價指標Ui為保障過程輸出參數在Xi的條件方差V[E(Y|Xi)]與輸出參數方差V(Y)之比[13－14]，公式如下:

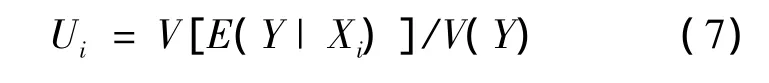
2 保障活動時間不確定性重要度計算

2.1 基于GERT的保障過程隨機網絡模型

由不同邏輯關系的保障活動構成的保障過程是一種典型的隨機網絡[15].因此，本文選用隨機網絡的圖示評審技術對保障過程進行建模.保障時間是保障過程的一個重要輸出表現.保障過程GERT模型的輸入是構成保障過程的保障活動的相關參數，輸出為保障過程工期.依據以下4個步驟對保障過程進行建模.

1)分析保障活動間邏輯關系，依據GERT不同的節點類型構建保障過程隨機網絡圖.

2)收集各項保障活動的基本參數:活動的發生概率和活動時間的概率分布，計算節點間傳遞函數Wij(s).

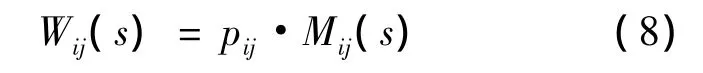
式中，pij為活動(i，j)在前導節點i實現的條件下發生的概率;Mij(s)為該活動(i，j)所費時間的矩母函數.活動(i，j)等價傳遞過程如圖1所示.

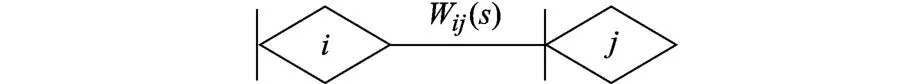
圖1 GERT網絡基本單元

3)分析網絡中參數傳遞線路和回路，利用梅森公式確定保障過程GERT網絡的等價傳遞函數WE(s).

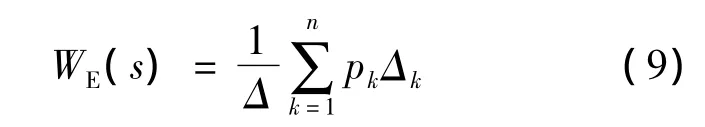
式中，pk為由節點i到節點j第k條路徑上的傳遞函數;Δk為消去與第k條路徑有關的全部節點和箭線后剩余子圖的特征式;Δ為網絡圖的特征式[16].

這里WE(s)是保障過程隨機網絡實現概率pE與保障過程工期矩母函數ME(s)之積.即

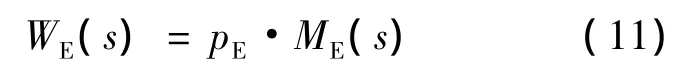
具有以下性質[17]，當s=0時，

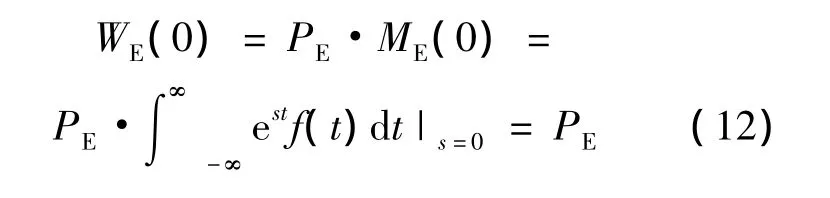
4)依據式(14)計算保障過程工期的矩母函數ME(s)，對ME(s)求導，得到保障過程工期期望值E(t)和.

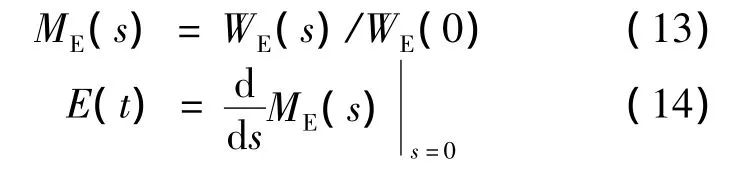
2.2 保障時間不確定性分析

用Ai表示某個待分析的保障活動，當保障過程輸出為總工期T時，式(7)可表示為保障活動工期方差V(Ti)與保障過程總工期方差V(T)的比值.

由矩母函數ME(s)性質可知

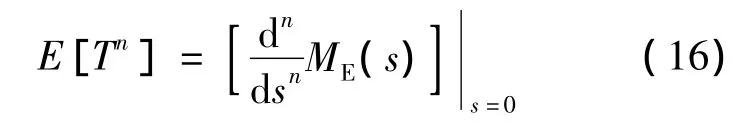
保障過程工期的方差V(T)可表示為

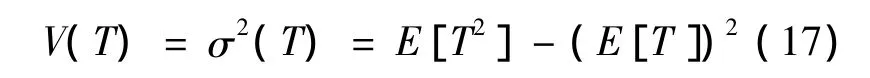
其中，E[T]為保障過程工期期望;E[T2]為保障過程工期平方的期望.

給定一個保障活動Ai時間分布的方差i'，則有一個不同的活動時間矩母函數M'ij(s)，相應有一個保障過程總工期的方差V(Ti).得到

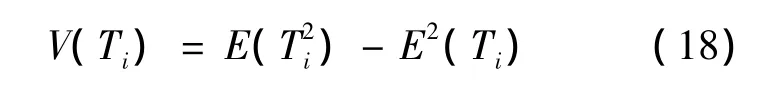
綜上所述，當輸入是保障活動不確定參數，輸出是保障過程總工期，保障過程不確定性分析步驟如圖2所示.

圖2 保障時間不確定分析方法

3 案例應用分析

航母艦載機的航空保障是一個典型的復雜、不確定的保障過程.在這一保障過程中主要包括以下保障活動[18]:飛行前的檢查;補充燃料、滑油、特種液體和氣體;充電;起飛、降落保障;艦面、機庫調度;維修保障等.艦載機保障過程如圖3所示.在這些保障過程中，一些保障活動的發生具有不確定性，如降落后飛機可能出現故障需要維修，根據故障情況可能需要船員級維修或者中繼級維修;彈射前飛行員開機檢查有可能出現故障情況.這里為便于計算簡化，假設這些保障活動時間均服從正態分布.艦載機航空保障作業轉化為GERT網絡，如圖4所示.

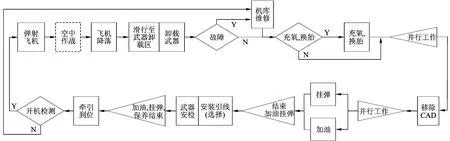
圖3 艦載機航空保障過程

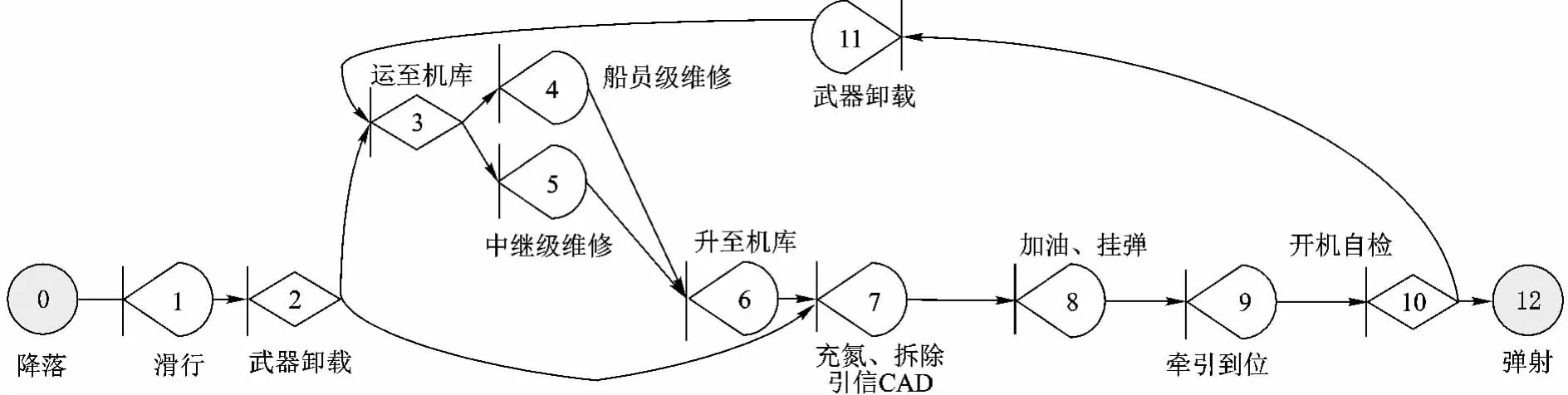
圖4 艦載機航空保障作業隨機網絡模型

本文結合美軍某次航母高強度演習F/A-18的統計數據，各活動時間參數分布及其矩母函數如表1所示[19].

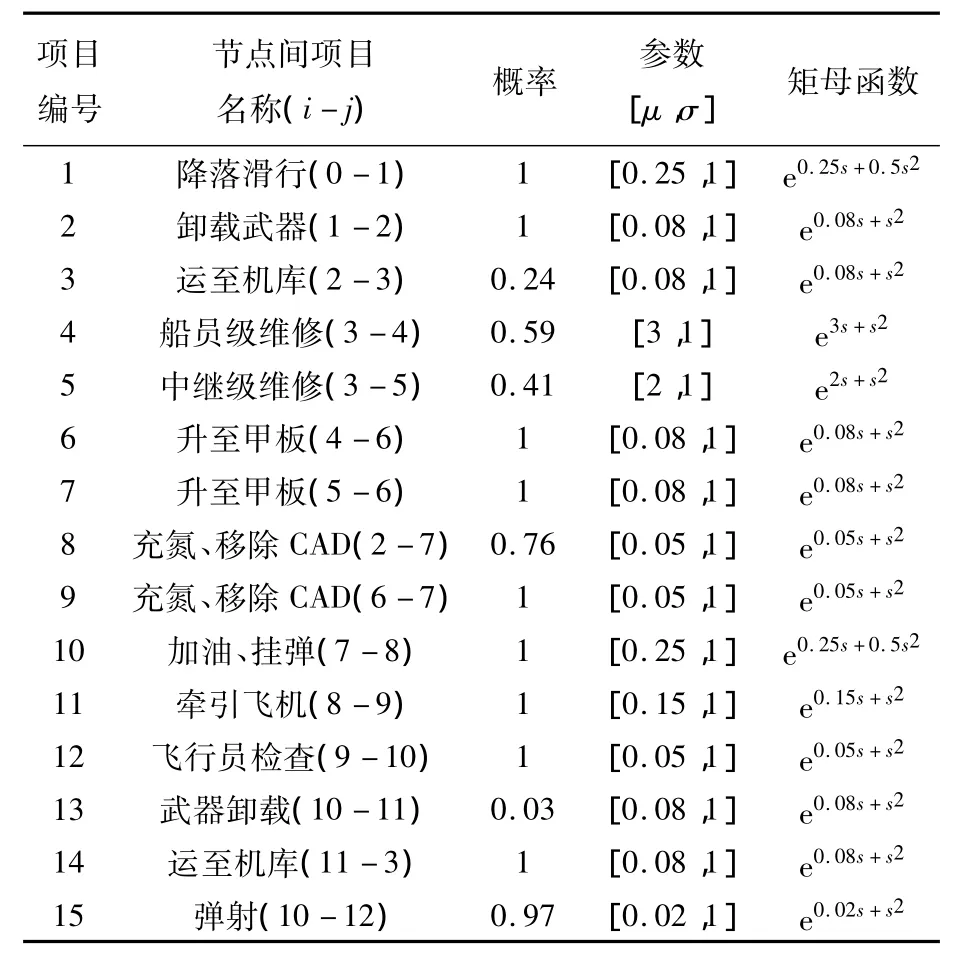
表1 艦載機航空保障作業活動參數表

利用式(9)計算0→12等價傳遞函數為

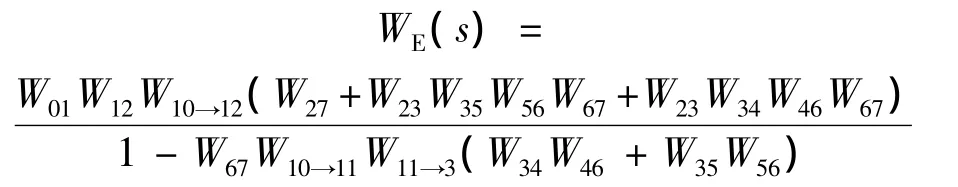
求得保障過程總工期方差V(T)=8.124

為每個保障活動工期方差的變動引起的保障過程工期方差變化，這里做出以下假設:

1)保障活動方差由1變為0;

2)保障活動方差由1變為0.5.

得到這兩種變化的相關數據如下表2所示.

表2 保障活動工期不同方差不確定性分析

保障活動工期方差不同變化量下對保障過程工期影響對比如圖5所示.

從圖中可以得到以下結論:

1)第一種情況(方差由1變為0)和第二種情況(方差由1變為0.5)保障工期的變化曲線基本一致，說明保障過程輸入變化對輸出不確定性影響是相對穩定的.

2)第一種情況下保障工期Ui整體高于第二種情況，如對于活動1，第一種情況下Ui大于第二種情況下Ui.說明保障活動工期方差波動對工期方差影響是成正比的，活動工期方差波動越大，整個保障過程工期方差變化越大.

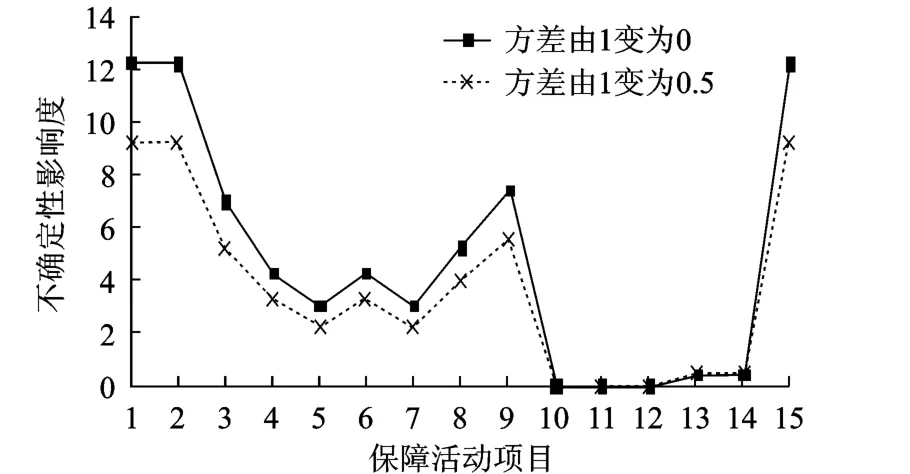
圖5 保障活動工期方差不同變化Ui值對比

4 結束語

保障過程的不確定性分析對于找到影響保障過程的敏感性因素有重要作用.本文通過對保障過程的敏感性分析，提出了保障過程的不確定性重要度指標，并設計了一種基于方差的保障時間不確定性全局分析方法;利用保障過程的隨機網絡模型，結合GERT解析算法，給出保障時間為不確定輸出、保障活動的發生概率和時間隨機分布作為不確定輸入條件下該方法的求解過程;以航母艦載機航空保障為案例，驗證了該方法的有效性.

References)

[1]王學望，康銳，張偵英，等.任務驅動的保障活動時間優化[J].計算機集成制造系統，2010，16(10):2227－2232

Wang Xuewang，Kang Rui，Zhang Zhenying，et al.Task driven support activity time optimization[J].Computer Integrated Manufacturing Systems，2010，16(10):2227－2232(in Chinese)

[2]Apostolakis G E.How useful is quantitative risk assessment?[J]Risk Analysis，2004，24(3):515－520

[3]文佳，康銳，劉瑞，等.基于保障活動流程的保障設備需求量計算模型[J].系統工程與電子技術，2010，32(09):1903－1906

Wen Jia，Kang Rui，Liu Rui，et al.Quantitative forecast model of support equipment based on support activity flow[J].Systems Engineering and Electronics，2010，32(09):1903－1906(in Chinese)

[4]王雷.裝備戰場搶修時間計劃研究[D].長沙:國防科學技術大學信息系統與管理學院，2010

Wang Lei.Research on time schedule plan for battle field damage assessment and repair[D].Changsha:School of Information System and Management，National University of Defense Technology，2010(in Chinese)

[5]Qiao Liu，Toshimitsu Homma.A new computational method of a moment-independent uncertainty importance measure[J]Reliability Engineering and System Safety，2009，94(1):1205－1211

[6]Campolongo F，Tarantola S，Saltelli A.Tackling quantitatively large dimensionality problems[J].Computer Physics Communications，1999，117(2):75－85

[7]Morris M D.Factorial sampling plans for preliminary computational experiments[J].Technometrics，1991，33(2):161－174

[8]Saltelli A，Tarantola S，Campolongo F.Sensitivity analysis as an ingredient of modeling[J].Statistical Science，2000，15(4):377－395

[9]Saltelli A.Sensitivity analysis for importance assessment[J].Risk Analysis，2002，22(3):579－590

[10]Helton J C，Davis F J，Johnson J D.A comparison of uncertainty and sensitivity analysis results obtained with random and Latin hypercube sampling[J].Reliability Engineering and System Safety，2005，89(3):305－330

[11]Patelli E，Pradlwarter H J，Schuёller G I.Global sensitivity of structural variability by random sampling[J].Computer Physics Communications，2010，181(12):2072－2081

[12]Borgonovo E.A new uncertainty importance measure[J].Reliability Engineering and System Safety，2007，92(6):771－784

[13]Tarantola S，Gatelli D，Mara T A.Random balance design for the estimation of first order global sensitivity indices[J].Reliability Engineering and System Safety，2006，91(6):717－727

[14]Homma T，Tomita K，Hato S.Uncertainty and sensitivity studies with the probabilistic accident consequence assessment code OSCAAR[J].Nuclear Engineering and Technology，2005，37(3):245－257

[15]馮強，曾聲奎，康銳.基于MAS的艦載機動態調度模型[J].航空學報，2009，30(11):2119－2125

Feng Qiang，Zeng Shengkui，Kang Rui.A MAS-based model for dynamic scheduling of carrier aircraft[J].Chinese Journal of Aeronautics，2009，30(11):2119－2125(in Chinese)

[16]Pritsker A A B.GERT graphical evaluation and review technique[M].Santa Monica，CAL，USA:Rand Corporation，1966

[17]Whitehouse G E.Systems analysis and design using network techniques[M].Englewood Cliffs，New Jersey:Prentice-Hall，1973:243－250

[18]Jewel A.Sortie generation capacity of embarked airwings[R].ADA359178，1998

[19]Jewell A，Wiggle M A，Gagnon C M，et al.USS nimitz and carrier airwing nine surge emonstration[R].ADA362472，1998