數學課堂教學情境的創設

在初中數學教學中，創設生活化的課堂教學情境有著很重要的作用，能夠激發初中生的學習興趣和求知欲，對提高課堂教學效率意義重大。

新課標要求，課堂教學要以學生為主體，以一切為了學生的發展為目標。創設多樣化的課堂教學情境可以讓學生感受到數學就在我們身邊，體現數學的實用性，激發學生的學習興趣。下面我結合自己的教學經驗談談教學情境的創設方式。

1.創設活動型情境

在教學《三角形全等的判斷條件》時，我創設了以下幾個活動情境。

活動一：讓學生把紙對折，然后剪下一個三角形，展開后把它照折痕剪下變成兩個三角形，問：這兩個三角形全等嗎？引導學生得出：完全重合的兩個三角形是全等三角形。提供動手操作的時間和空間，體現“教師是主導，學生是主體”的新課程理念。

活動二：把活動一制作的兩個三角形重合，問：全等的兩個三角形是不是任意擺放都會重合？引導學生達成共識：兩個三角形是否全等與三角形的三邊和三個角有關，在動手操作過程中理解三角形是否全等與六組元素有關。

活動三：讓學生畫圖討論，兩個三角形中至少要有幾個元素分別對應相等，兩個三角形才能全等。引導學生分類討論，可分成一個元素，兩個元素，三個元素，四個元素，五個元素，六個元素。此活動的目的是培養學生的分類思想，讓數學思想在教學中體現出來。

在教學《多項式與多項式相乘》時，我創設了以下情境：給每一個學習小組分發一組紙片，讓學生根據手中的紙片拼圖比賽，讓學生動手實踐理解新知識，展示學生作品并拿出一種拼法，讓學生寫出幾何意義。學生寫出以下四種表達式：（1）（m+n）（a+b），（2）（m+n）a+（m+n）b，（3）ma+mb+na+nb，（4）m（a+b）+n（a+b），提問：（1）（2）（3）（4）有什么關系？學生得出（m+n）（a+b）=（m+n）a+（m+n）b=ma+mb+na+nb=m（a+b）+n（a+b），引導學生將以上式子分解為（m+n）（a+b）=（m+n）a+（m+n）b。

2.創設問題型情境

在教學中創設問題型情境，能激起學生的求知欲望，感受到發現的樂趣。

在教學《三角形全等的判斷條件》時，我提出以下幾個問題。問題一：電改時期要在河的兩邊立兩根電線桿，并且引上電線，但是河的兩邊不能直接測量長度，你們有辦法嗎？問題二：有一組對應相等的元素的兩個三角形全等嗎？問題三：有兩組元素對應相等的三角形能全等嗎？有幾種可能情況？引導學生得出有兩角，兩邊，一邊一角的情況。

《多項式與多項式相乘》授課時，我讓班上兩個同學畫出家里廚房的平面圖，提問學生：你能計算出廚房的面積嗎？接著提出問題一：你能求出m（a+b）的值嗎？引導學生根據單項式乘以多項式得出m（a+b）=ma+mb，通過求m（a+b）復習舊的知識。問題二：你能用圖形表達出m（a+b）=ma+mb的幾何意義嗎？問題三：你能用圖形表達出（m+n）（a+b）嗎？如果不能，則困難是什么？

3.創設社會問題型情境

學生雖然沒有這個能力解決社會問題，但社會問題最能集中學生的注意力，也最能激發學生的學習興趣。

在教學《角平分線》時，可以給學生講這樣的故事：安溪縣建中國茶都時，縣政府為了選址問題向各界人士征集方案，條件是：中國茶都必須選在運輸方便的地方（安溪縣當時有與外界疏通的公路和鐵路），問學生：你能給縣政府提出方案嗎？

4.創設猜想型情境

在教學《直角三角形全等》時，創設問題情境：舞臺背景的形狀是兩個直角三角形，為了美觀，這兩個直角三角形必須一模一樣，你能幫忙想個辦法嗎？可以引導學生猜想1：兩直角邊一樣時，這兩個直角三角形必須一模一樣。猜想2：短的直角邊與斜邊一樣時，這兩個直角三角形必須一模一樣。猜想3：長的直角邊與斜邊一樣時，這兩個直角三角形必須一模一樣。

為了驗證猜想是否成立，可以讓學生先作圖再證明。這樣不但使學生獲得了更多的知識和信息，更重要的是改變了學生的學習方式，開拓了學生的思維，讓學生感受到數學的無窮魅力。

5.創設探究型情境式

教師可創設有價值的問題情境，引起學生的爭論，培養學生質疑、探究的習慣，提高分析能力。

在教學《平移的特征》時，探究一：探索平移的特征1。設問：平移過程中圖形有變化嗎？引導學生發現平移后的圖形與原來的圖形的對應線段平行且相等，對應角相等，圖形的形狀、大小都沒有發生變化。

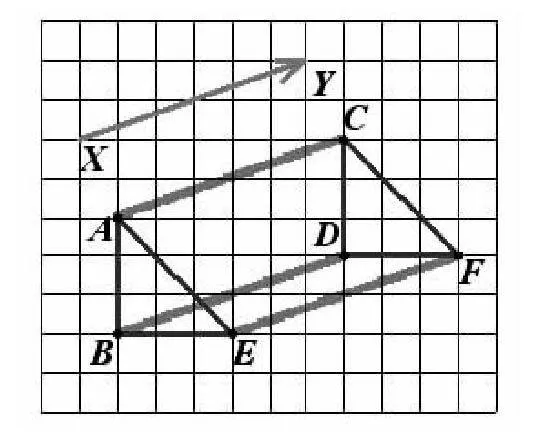
探究二：平移的特征2。（1）△ABE沿著XY的方向平移到△DCF，如何移動？

（2）A，B，E的對應點分別是什么？

（3）量出AC，BD，EF的長度，量出各個角的大小。

（4）可以發現AC=BD=EF，∠ABD+∠BAC=180°，∠EAC+∠AEF=180°。

探索的目的是達成共識：平移的特征2，平移后對應點所連的線段平行并且相等，讓學生參與并經歷整個探索過程，體會發現的樂趣。

總之，創設課堂教學情境的方法很多，老師要因地制宜，合理使用，努力使創設的數學教學情境具有新意，讓學生體會到學習的樂趣。

參考文獻：

[1]王磊.實施創新教育，培養創新人才——訪中央教科所所長閻立欽教授.教育研究，1999.7.5.

[2]柴俊.數學教育個案學習學習.2003.

[3]王蕾.數學教學中加強技能訓練的嘗試.師范教育，1999.7：8-58.