圖像法巧解2013年重慶高考物理卷壓軸題

胡先進 李 力

(1.重慶市實驗中學，重慶 401320;2.重慶清華中學，重慶 400054)

2013年是重慶進入新課改后按照新課標高考的第一年.其中的物理試題精彩之處很多，例如 1、4、7、8(2)、9、10(2)等題都很值得回味，全卷有力地體現了“以知識為載體、從能力立意”的高考命題原則.

圖1

題目.在一種新的“子母球”表演中，讓同一豎直線上的小球A和小球B，從距水平地面的高度為ph(p＞1)和h的地方同時由靜止釋放，如圖1所示.球A的質量為m，球B的質量為3m.設所有碰撞都是彈性碰撞，重力加速度大小為g，忽略球的直徑、空氣阻力及碰撞時間.

(1)求球B第1次落地時球A的速度大小;(2)若球B在第1次上升過程中就能與球A相碰，求p的取值范圍;(3)在(2)情形下，要使球A第1次碰后能到達比其釋放點更高的位置，求p應滿足的條件.

此題以“子母球碰撞”(也稱“彈弓效應”)演示實驗為背景，通過彈性碰撞和追及相遇所涉及的能量守恒、動量守恒、勻變速運動學公式等重要知識點，著重考查了閱讀理解能力、分析綜合能力和應用數學處理物理問題的能力.第(3)小題有相當難度，不少師生反映高考評分答案的解法和通常的解答均顯得過于繁瑣.鑒于此，本文給出一種直觀簡捷的巧解.為方便計，以下直接探討第(2)、(3)小題.

解析:(2)顯然，p=1時，球B在反彈離地瞬間與球A相碰.

(3)仍取向下為速度正向，考慮碰后A球正好返回原處的臨界情況，此時要求vA'=-vA，代入動量守恒和能量守恒方程，得

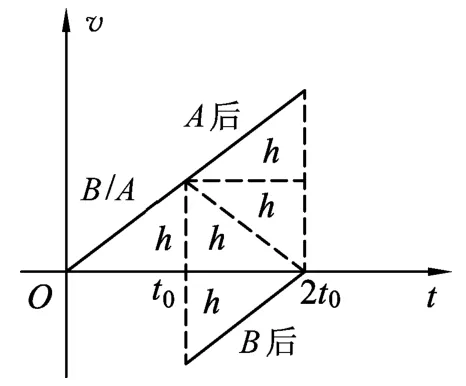
圖2

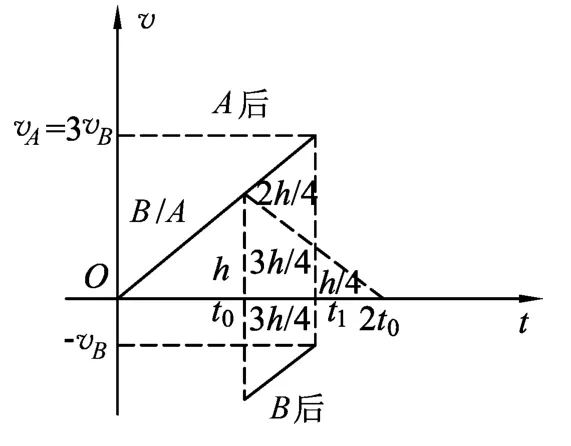
圖3

由后式得vB'=-vB(vB'=vB舍去)，代入前式有vA=3vB，可知在圖2中的t1=1.5t0時刻碰撞，由圖得xA+xB=(h+3h/4+2h/4)+3h/4=ph，故p=3.從圖3還看出，若碰撞時刻t1從1.5t0起越靠近t0，則越有vA＜3vB，這時碰后|vA'|＞|-vA|，從而球A碰后能到達比其釋放點更高的位置，而t1→t0時顯然有p=1.

綜上所述，當1＜p＜3時，球A第1次碰后能到達比其釋放點更高的位置.