季節(jié)性SARIMA模型在實(shí)驗(yàn)室開放管理中的應(yīng)用
王法玉, 王靜超
(天津理工大學(xué) 計算機(jī)實(shí)驗(yàn)教學(xué)示范中心; 智能計算及軟件新技術(shù)重點(diǎn)實(shí)驗(yàn)室, 天津 300384)
0 引 言
高校實(shí)驗(yàn)室是高校從事實(shí)驗(yàn)教學(xué)、進(jìn)行人才培養(yǎng)的重要場所[1]。為了進(jìn)一步培養(yǎng)大學(xué)生的創(chuàng)新和實(shí)踐能力,近年來,各高校紛紛建立了創(chuàng)新實(shí)驗(yàn)室,為學(xué)生提供課外第二課堂創(chuàng)新實(shí)踐平臺[2]。工程類實(shí)驗(yàn)教學(xué)不僅是教學(xué)的重要的組成部分,多樣性的實(shí)驗(yàn)教學(xué)和開放性實(shí)驗(yàn)室也是教育改革的一項基本任務(wù)[3-5]。目前大多數(shù)學(xué)校都在實(shí)施實(shí)驗(yàn)室開放,對實(shí)驗(yàn)室管理也做了很多研究,并開發(fā)了一些實(shí)驗(yàn)室開放管理系統(tǒng),但是多數(shù)管理系統(tǒng)都是只注重便捷,而對資源的利用率的研究比較少。
為了給學(xué)生提供一個開放自由的學(xué)習(xí)環(huán)境和足夠的學(xué)習(xí)資源,培養(yǎng)學(xué)生的創(chuàng)新實(shí)踐能力,我院自2000年以來實(shí)施了實(shí)驗(yàn)室開放政策,得到了廣大學(xué)生的歡迎,學(xué)生的學(xué)習(xí)熱情更加濃厚。但在實(shí)驗(yàn)室管理上,實(shí)驗(yàn)室上機(jī)人數(shù)的隨機(jī)性和值班人員如何安排,卻難以權(quán)衡,為了充分滿足學(xué)生的需求,值班人員配備和開放實(shí)驗(yàn)室數(shù)量總是大于實(shí)際需求,造成值班人員安排和實(shí)驗(yàn)房間開放的數(shù)量難以確定,造成人力、物力和財力的浪費(fèi)。為了更加有效利用和挖掘?qū)嶒?yàn)室資源,提高實(shí)驗(yàn)室和實(shí)驗(yàn)設(shè)備的利用率[6]。通過對幾年來的實(shí)驗(yàn)室上機(jī)人數(shù)研究,發(fā)現(xiàn)實(shí)際的上機(jī)人數(shù)具有長期相關(guān)性, 也稱自相似性, 即統(tǒng)計意義下的自相似性,具有成長性[7]。因此,本文利用時間序列分析法對實(shí)驗(yàn)室日常上機(jī)人數(shù)進(jìn)行分析、研究和建模,進(jìn)而對上機(jī)人數(shù)進(jìn)行預(yù)測,旨在通過合理安排值班人員和開放實(shí)驗(yàn)室數(shù)量,達(dá)到節(jié)約資源的目的。
1 理論基礎(chǔ)
時間序列分析是處理動態(tài)數(shù)據(jù)的一種比較有效的時域分析方法,通過觀察動態(tài)數(shù)據(jù)的變化規(guī)律,對數(shù)據(jù)進(jìn)行擬合,并對未來數(shù)據(jù)做出預(yù)測。在許多實(shí)際問題中,所觀測到的數(shù)據(jù)序列{xt}常不是平穩(wěn)序列,但如果將其做有限次差分處理后,可轉(zhuǎn)化差分序列{Sn},是平穩(wěn)序列,那么可用平穩(wěn)信號序列模型來做研究[8]。
1.1 ARIMA模型
自回歸移動平均(Auto-Regressive Integrated Moving Average,ARIMA)模型是由美國統(tǒng)計學(xué)家Box 和Jenkins 共同提出的,又叫B-J 模型[9]。該模型擬合的是差分平穩(wěn)序列,實(shí)際上就是差分運(yùn)算和ARMA 模型的結(jié)合。其基本建模思想和建模步驟可總結(jié)為:① 通過差分使非平穩(wěn)過程變成平穩(wěn)過程;② 建立描述該平穩(wěn)過程的合適模型;③ 使用構(gòu)建好的模型,預(yù)測將來值。ARIMA 模型是時間序列分析中重要的模型之一,目前廣泛應(yīng)用于各種領(lǐng)域[10-12]。
假設(shè){xt/t=0,1,…}為非平穩(wěn)隨機(jī)序列,則ARIMA的一般形式為:

(1)
其中:
Φ(B)=1-φ1B-φ2B2-…-φpBp
Θ(B)=1-θ1B-θ2B2-…-φqBq

1.2 季節(jié)性SARIMA模型
季節(jié)性SARIMA 建模是在ARIMA 模型基礎(chǔ)上發(fā)展起來的,用于具有周期性變化的序列的建模。在周期內(nèi),它提取當(dāng)前時刻數(shù)據(jù)與前期數(shù)據(jù)的關(guān)聯(lián)特征;在周期間,它提取當(dāng)前時刻數(shù)據(jù)與前幾個周期相同時刻的數(shù)據(jù)的關(guān)聯(lián)特征[13]。將周期內(nèi)特征和周期間特征結(jié)合起來,更加全面地描述序列的變化規(guī)律,得到的模型,對于序列變化情況的刻畫也更加準(zhǔn)確。因此,使用季節(jié)ARIMA 模型對季節(jié)性數(shù)據(jù)進(jìn)行研究也是目前時序分析的熱點(diǎn)[14-16]。

(2)
Θ(Bs)=1-Θ1Bs-Θ2B2s-…-ΘpBps
Φ(Bs)=1-Φ1Bs-Φ2B2s-…-ΦqBqs
式(2)的模型中季節(jié)差分僅僅消除了周期間相同周期點(diǎn)之間具有的相關(guān)部分,時間序列還可能存在長期趨勢,一個周期內(nèi)的不同周期點(diǎn)之間也具有一定的相關(guān)性,因此,由式(1)、(2)可得季節(jié)性ARIMA(p,d,q)(P,D,Q)s模型為:
1.3 ADF檢驗(yàn)
ADF(Augmented Dickey-Fuller)檢驗(yàn)是增項DF檢驗(yàn),ADF檢驗(yàn)不僅可以檢驗(yàn)AR(1)的平穩(wěn)性,而且可以檢驗(yàn)AR(P)過程的平穩(wěn)性。
對于任意AR(P)過程,
Xt=φ1Xt-1+…+φpXt-p+εt
(3)
如果方程所有特征根都在單位圓內(nèi),則序列平穩(wěn);如果有一個特征根存在且為1,則序列為非平穩(wěn)序列。
對式(3)進(jìn)行變形簡化后得:

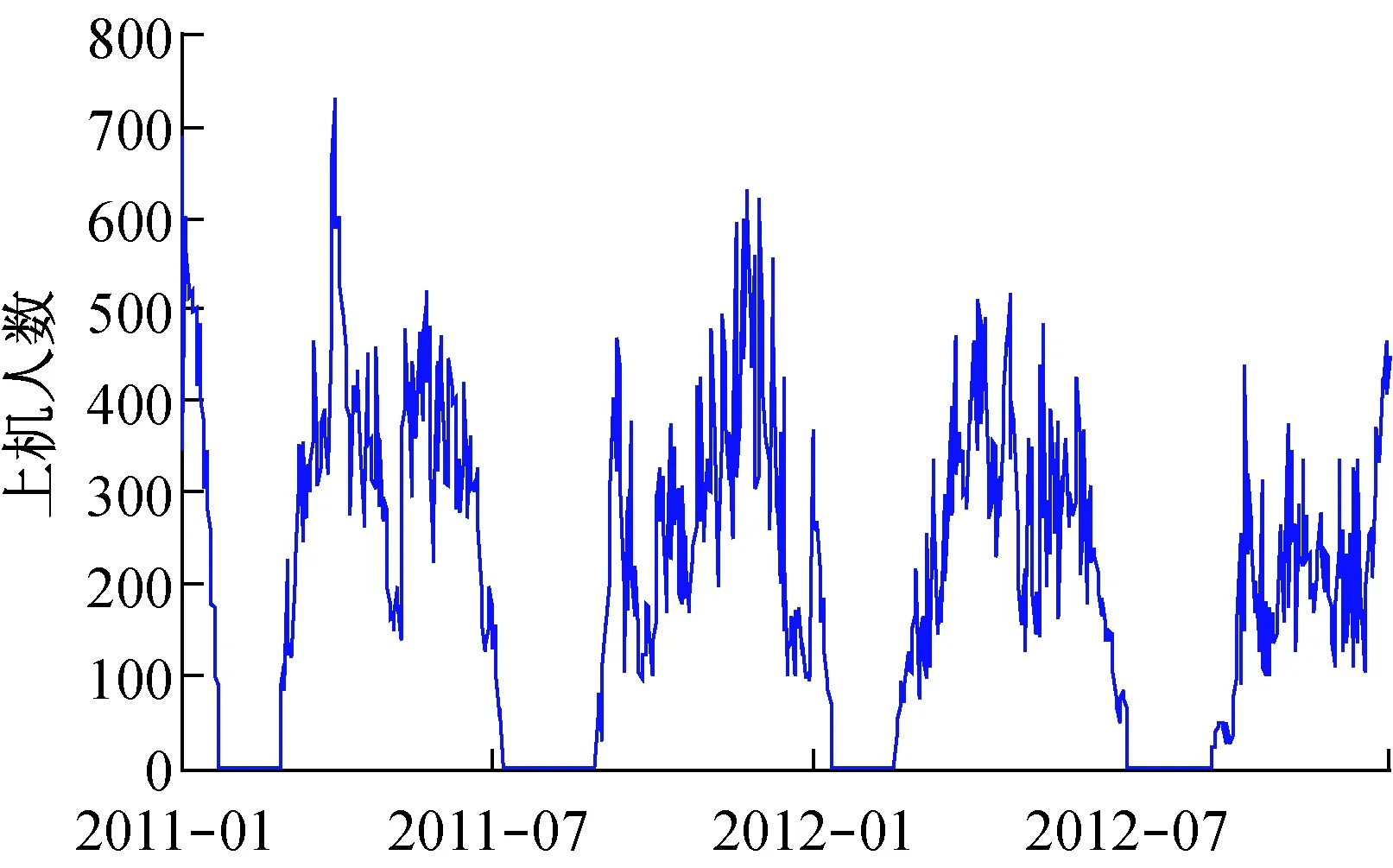
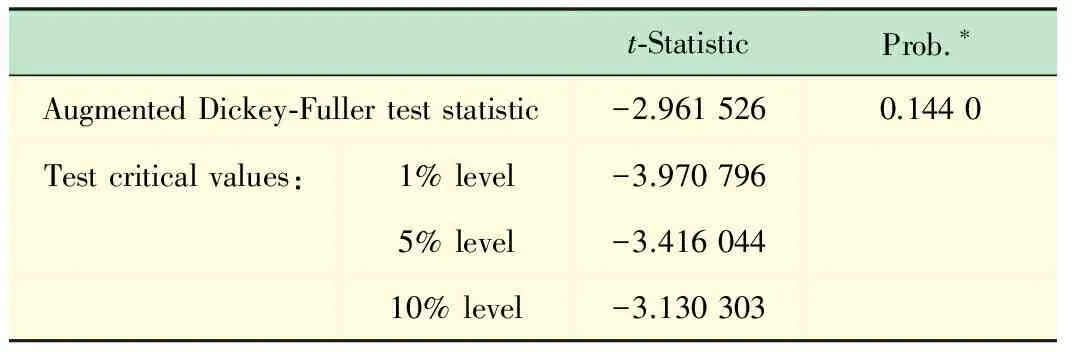
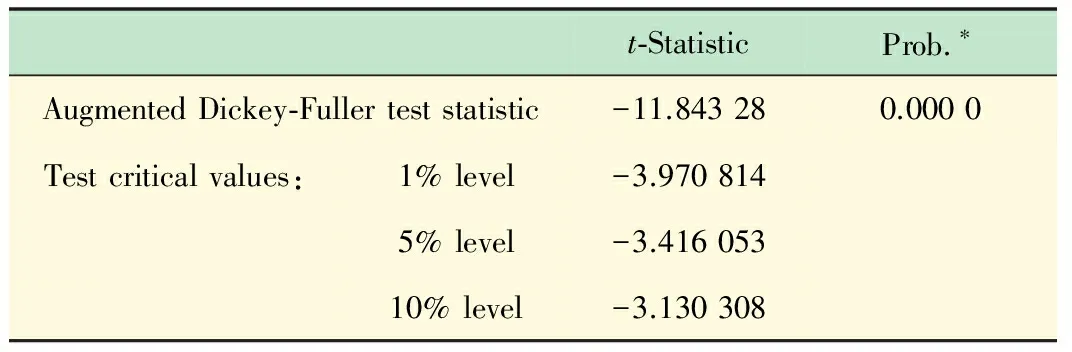
H0∶ρ=o?H1∶ρ 構(gòu)造ADF檢驗(yàn)統(tǒng)計量: 通過Monte Carlo方法,可以得到ADF檢驗(yàn)統(tǒng)計量的臨界值表。 本文在季節(jié)性SARIMA模型構(gòu)建過程中主要分為以下幾步: (1) 平穩(wěn)性檢驗(yàn)。檢驗(yàn)時間序列的平穩(wěn)性,即確定d、D的大小,最直觀的識別方法是自相關(guān)圖法。如果自相關(guān)系數(shù)迅速趨于零,即自相關(guān)系數(shù)具有截尾性,則時間序列為平穩(wěn)時間序列;如果時間序列存在一定的趨勢性,則需要對原序列進(jìn)行差分處理;如果時間序列存在異方差性,則需先對數(shù)據(jù)進(jìn)行對數(shù)轉(zhuǎn)換。 (2) 模型識別。模型識別即確定相應(yīng)季節(jié)ARIMA模型的階數(shù)p、q、P、Q的取值。一般情況下,可通過觀察相關(guān)圖估計模型階數(shù)p、q、P、Q的可能取值,然后通過AIC、SC準(zhǔn)則等,確定最合適的模型階數(shù),AIC值和SC值都是越小越好。 (3) 用最小二乘法進(jìn)行模型估計。最小二乘法估計是線性模型中最常用的估計方法,具有良好的統(tǒng)計性質(zhì),且計算簡便。 (4) 白噪聲檢驗(yàn)。對殘差進(jìn)行白噪聲檢驗(yàn),由定義可知白噪聲序列的任意兩個時序值之間都是完全不相關(guān)的。但在實(shí)際中,完全的不相關(guān)是不可能的。由于序列的長度都是有限的,故自相關(guān)系數(shù)不可能都是零。可以認(rèn)為自相關(guān)系數(shù)總是在零附近上下浮動,且浮動的范圍有非常界限的序列為白噪聲序列。為了定量準(zhǔn)確的判斷是否純隨機(jī),Bartlett給出了統(tǒng)計的方法驗(yàn)證序列的白噪聲性,此時是將自相關(guān)系數(shù)放在一起進(jìn)行整體檢驗(yàn)。Bartlett提出如果一個時間序列是白噪聲序列,則提取一個觀察個數(shù)為n的序列,那么該序列的延遲非零期的樣本自相關(guān)系數(shù)將近似服從均值等于零,方差近似為觀察序列個數(shù)倒數(shù)的正態(tài)分布。 (5) 預(yù)測。本文用Eviews6.0實(shí)現(xiàn)整個建模過程,Eviews軟件是美國QMS公司推出的計量經(jīng)濟(jì)學(xué)軟件,在對時間序列的數(shù)據(jù)進(jìn)行分析,建立序列間的統(tǒng)計關(guān)系式,并用該關(guān)系式進(jìn)行預(yù)測、模擬等。 圖1為2011年1月~2012年11月我院實(shí)驗(yàn)室日常上機(jī)人數(shù)時序圖,該時序圖以天為單位,實(shí)驗(yàn)環(huán)境是Eviews6.0。由圖1可以看出日常上機(jī)人數(shù)隨機(jī)性很大, 觀測值序列呈現(xiàn)周期性[16],可初步斷定該序列為非平穩(wěn)序列。 圖1 日常上機(jī)人數(shù)時序圖 為了進(jìn)一步檢驗(yàn)序列的平穩(wěn)性, 本文對原序列進(jìn)行ADF檢驗(yàn),即如果方程所有特征根都在單位圓內(nèi),則序列平穩(wěn),如果有一個特征根存在且為1,則序列為非平穩(wěn)序列。ADF檢驗(yàn)結(jié)果如表1所示。 由表1的結(jié)果可以看出,在10%的顯著性水平下可以接受原假設(shè),即原序列有一個單位根,故可以斷定原序列具有非平穩(wěn)性。 表1 ADF檢驗(yàn)結(jié)果 從圖1中可以看出,在每年的5月份和11月份都會有一段連續(xù)的峰值出現(xiàn),表明此段時間內(nèi)實(shí)驗(yàn)室上機(jī)人數(shù)較多。而8、2月份基本為零,因?yàn)檫@2個月為放假時間。可初步斷定周期為6個月,有相關(guān)圖可得周期為182天。 在一般情況下,周期性序列的季節(jié)性差分次數(shù)不會超過1[9]。因此,我們首先進(jìn)行一階差分消除趨勢特征,再進(jìn)行182步周期差分消除周期信息,并對差分后的序列進(jìn)行ADF檢驗(yàn),結(jié)果如表2。 表2 差分序列ADF檢驗(yàn)結(jié)果 由表2中的P值可以判斷出,在10%的顯著性水平下拒絕原假設(shè),即序列對象不存在單位根。因而上機(jī)人數(shù)是1階單整,故SARIMA模型的d=1。 通過差分后序列AC和PAC,判斷SARIMA模型的階數(shù)p、q、P、Q。由表3可以看出,AC 為一階截尾,可令q=1。另外,在t=182處,PAC顯著不為0,因此,可令P=1。同樣觀察偏相關(guān)系數(shù),可以看出,p在8階截尾,可得p=8。在t=182處,AC顯著為0,因此,可令Q=0。 在EVIEWS 6.0中,對模型進(jìn)行最小二乘法參數(shù)估計并利用模型對差分后的序列進(jìn)行擬合,經(jīng)過多次嘗試、篩選和剔除所有不顯著系數(shù),最終確定結(jié)果見表4。 白噪聲檢驗(yàn)結(jié)果如表5所示。由表可知,AC與PAC顯著趨于0,因而殘差序列不存在自相關(guān),是白噪聲序列,故構(gòu)建的模型是理想的,可用于預(yù)測。 表3 差分后序列相關(guān)圖 表4 最小二乘法參數(shù)估計結(jié)果 表5 殘差相關(guān)圖 最終可得模型為ARIMA(8,1,1)(1,1,0),表4為相應(yīng)參數(shù)的估計值。故模型方程為: (1-0.313B-0.268B2-0.151B7)(1+ 0.536B182)xt=(1-1.03B)εt 利用模型對2012年12月1日~15日進(jìn)行預(yù)測。 由表6可以看出,預(yù)測結(jié)果比較接近實(shí)際情況。自2012年開始對模型進(jìn)行研究,并應(yīng)用于我院實(shí)驗(yàn)室開放實(shí)際中,一年以來,實(shí)驗(yàn)室開放管理水平得到了很大提升。在毫不影響學(xué)生充分利用實(shí)驗(yàn)室設(shè)備的基礎(chǔ)上,為學(xué)院省下一部分財政支出,大大節(jié)約人、財、物的使用。減輕了工作人員的工作強(qiáng)度和工作時間。 ARIMA是一種計算簡便、計算精度較高、使用范圍很廣的時間序列預(yù)測模型。季節(jié)性SARIMA 模型在原有模型的基礎(chǔ)上擴(kuò)展了對周期性序列的應(yīng)用,使其范圍更加廣泛。本文利用季節(jié)性SARIMA模型,采用EVIEWS軟件對實(shí)驗(yàn)室日常上機(jī)人數(shù)進(jìn)行預(yù)測分析,是我院實(shí)驗(yàn)室開放管理的一部分,有效提高了實(shí)驗(yàn)室資源的利用率,方便學(xué)生學(xué)習(xí),同時節(jié)省了資源,使我校的實(shí)驗(yàn)室管理水平又上了一個臺階。希望本研究對于其他學(xué)校實(shí)驗(yàn)室開放管理給予一個啟發(fā)和借鑒。 表6 實(shí)際上機(jī)人數(shù)和預(yù)測人數(shù)對照表 [1] 蔡海燕,劉 昭.實(shí)驗(yàn)室信息化管理初探[J].實(shí)驗(yàn)室研究與探索,2010,29(11):373-375. CAI Hai-yan,LIU Zhao.Discussion on the Information Management of Laboratory[J]. Research and Exploration in Laboratory,2010, 29(11):373-375. [2] 王志軍,楊延軍.開放式教學(xué)實(shí)驗(yàn)室實(shí)時監(jiān)控系統(tǒng)[J].實(shí)驗(yàn)室研究與探索,2011,30(1):158-160. WANG Zhi-jun,YANG Yan-jun. Real Time Monitoring System for Open Teaching Labs[J]. Research and Exploration in Laboratory,2011, 30(1):158-160. [3] Alon Gany. The role of laboratory experiments in engineering education [C]//Proc ASME 2008 9th Biennial Conference on Engineering Systems Design and Analysis (ESDA2008). Haifa, Israel, pp. July 2008:645-647. [4] Richard Chiou, Michael Mauk, William Danley, Robin Kizirian. Innovative engineering technology curriculum integrated with web-based technology in robotics, mechatronics, and equality [C]//Proc ASME 2009 International Mechanical Engineering Congress and Exposition (IMECE2009). Lake Buena Vista, Florida, USA, pp. 2009: 369-376. [5] Frank K. Lu, Philip K. Panicker, M. Byron Webb. Introducing modern laboratory experiences to mechanical and aerospace engineering students [C]//Proc ASME 2007 International Mechanical Engineering Congress and Exposition (IMECE2007). Seattle, Washington, USA, pp. 2007:443-452. [6] 王法玉,張 樺.基于Web 與短信結(jié)合的實(shí)驗(yàn)室開放管理系統(tǒng)設(shè)計與實(shí)現(xiàn)[J]. 實(shí)驗(yàn)技術(shù)與管理, 2011,28(1):104-107. WANG Fa-yu,ZHANG Hua. Design and Implementation of Laboratory Opening Management system based on Web and SMS[J]. Experimental Technology and Management,2011,28(1):104-107. [7] 金 旗,裴昌幸,朱暢華.ARIMA 模型法分析網(wǎng)絡(luò)流量[J]. 西安電子科技大學(xué)學(xué)報(自然科學(xué)版),2003(2):6-10. JI Qi, PEI Chang-xing, ZHU Chang-hua. ARIMA analysis method in network traffic[J].Jouranl of Xidian University,2003(2):6-10. [8] 王宏禹. 非平穩(wěn)隨機(jī)信號分析與處理[M]. 北京: 國防工業(yè)出版社, 1999. 293-307. [9] 鄒柏賢,劉 強(qiáng).基于ARMA模型的網(wǎng)絡(luò)流量預(yù)測[J].計算機(jī)研究與發(fā)展,2002,39(12):1645-1652. ZOU Bo-Xian, LIU Qiang. ARMA-BASED TRAFFIC PREDICATION AND OVERLOAD DETECTION OF NETWORK[J].Journal of Computer Research and Development, 2002,39(12):1645-1652. [10] 楊建萍. 基于ARIMA 模型的用電量時間序列建模和預(yù)報[J]. 工程數(shù)學(xué)學(xué)報, 2008,25(4): 611-615. YANG Jian-Ping. ARIMA Time Series Modeling and Forecasting of Electricity Consumption[J]. Chinese Journal of Engineering Mathematics, 2008,25(4): 611-615. [11] 漆 莉,李 革,李 勤. ARIMA 模型在流行性感冒預(yù)測中的應(yīng)用[J]. 第三軍醫(yī)大學(xué)學(xué)報, 2007,29(3): 267-269. QI Li,LI Ge,LI Qin. Applications of ARMA model on predictive incidence of influenza[J].Acta Academiae Medicinae Militaris Tertiae, 2007,29(3): 267-269. [12] 韓 超, 宋 蘇, 王成紅. 基于ARIMA 模型的短時交通流實(shí)時自適應(yīng)預(yù)測[J]. 系統(tǒng)仿真學(xué)報, 2004, 16(7): 1530-1532. HAN Chao,SONG Su,WANG Cheng.A Real-time Short-term Traffic Flow Adaptive Forecasting Method Based on ARIMA Model[J].Journal of System Simulation,2004,16(7): 1530-1532. [13] 周 鑫,張 錦,李 果,等.基于乘積季節(jié)模型的GPRS小區(qū)流量預(yù)測[J]. 計算機(jī)工程,2010,36(18):76-78. ZHOU Xin, ZHANG Jin, LI Guo,etc.Traffic Prediction of GPRS Cells Based on Multiple Seasonal Model[J].Computer Engineering,2010,36(18):76-78. [14] 張 蔚, 張彥琦, 楊 旭. 時間序列資料ARIMA 季節(jié)乘積模型及其應(yīng)用[J]. 第三軍醫(yī)大學(xué)學(xué)報, 2002, 24(8): 955-957. ZHANG Wei,ZHANG YAN-qi,YANG Xu.Model of multiple seasonal ARIMA and its application ot data in time series[J]. Acta Academiae Medicinae Militaris Tertiae, 2002, 24(8): 955-957. [15] 張 偉, 張新波. 移動GSM網(wǎng)話務(wù)量的ARIMA模型的建立及其預(yù)測[J]. 數(shù)學(xué)理論與應(yīng)用, 2008, 28(2): 70-74. ZHANG Wei, ZHANGXin-bo. Modeling and predicting wirless GSM traffic load on the ARIMA model[J].Mathematical Theory and Applications, 2008, 28(2): 70-74. [16] Geoge E,Box P. 時間序列分析預(yù)測與控制[M]. 顧嵐主, 范金城,譯. 北京: 中國統(tǒng)計出版社, 1997:125-126.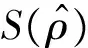
1.4 SARIMA模型建模步驟
2 實(shí)例應(yīng)用
2.1 平穩(wěn)性檢驗(yàn)
2.2 周期性確定
2.3 平穩(wěn)化處理
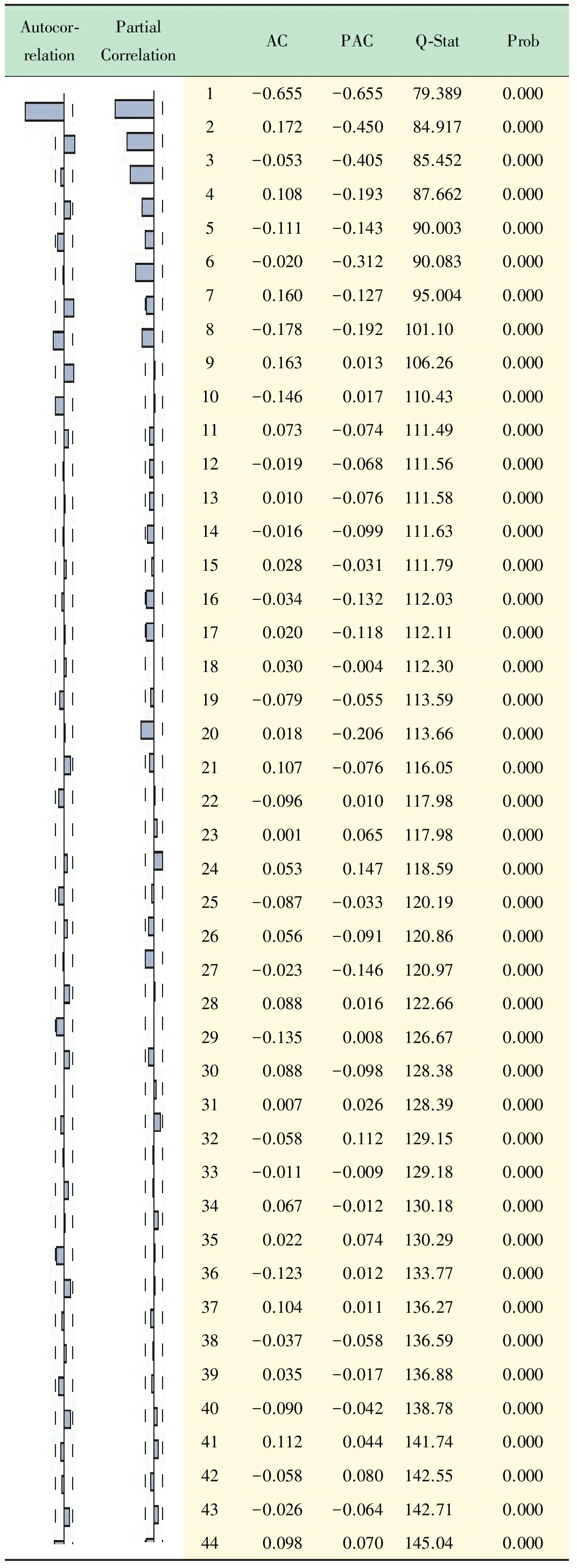
2.4 模型定階
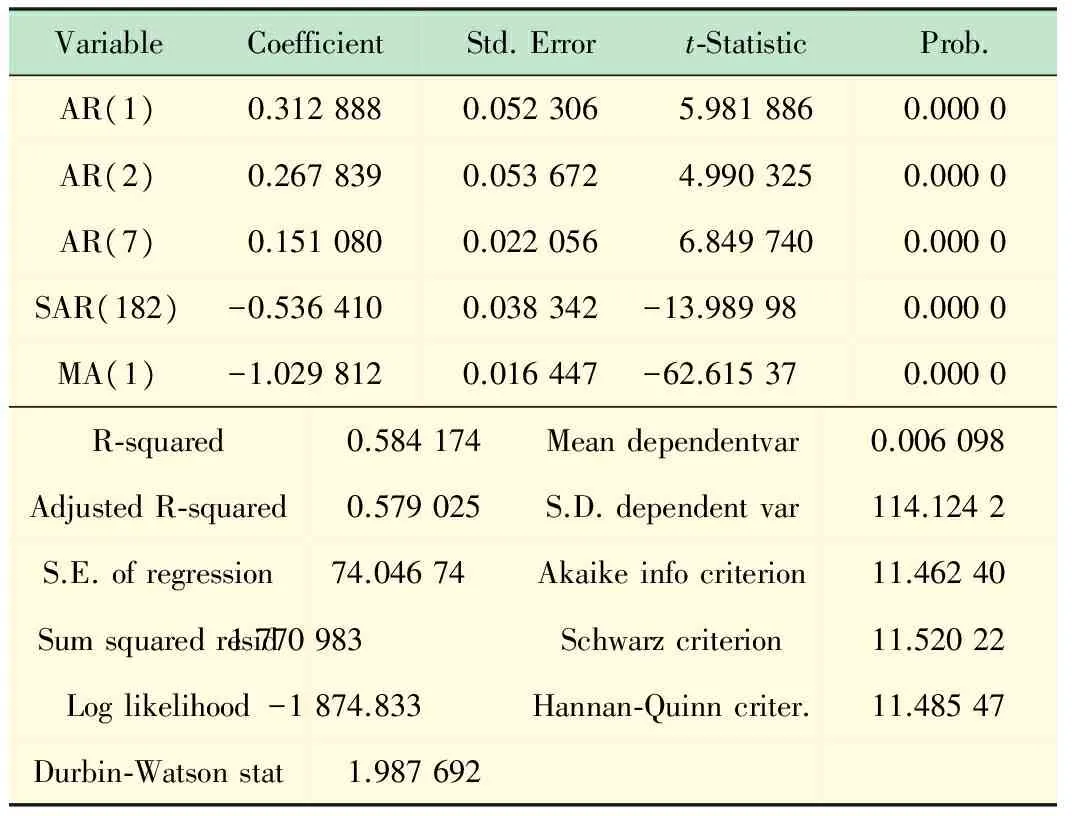
2.5 模型的建立與預(yù)測
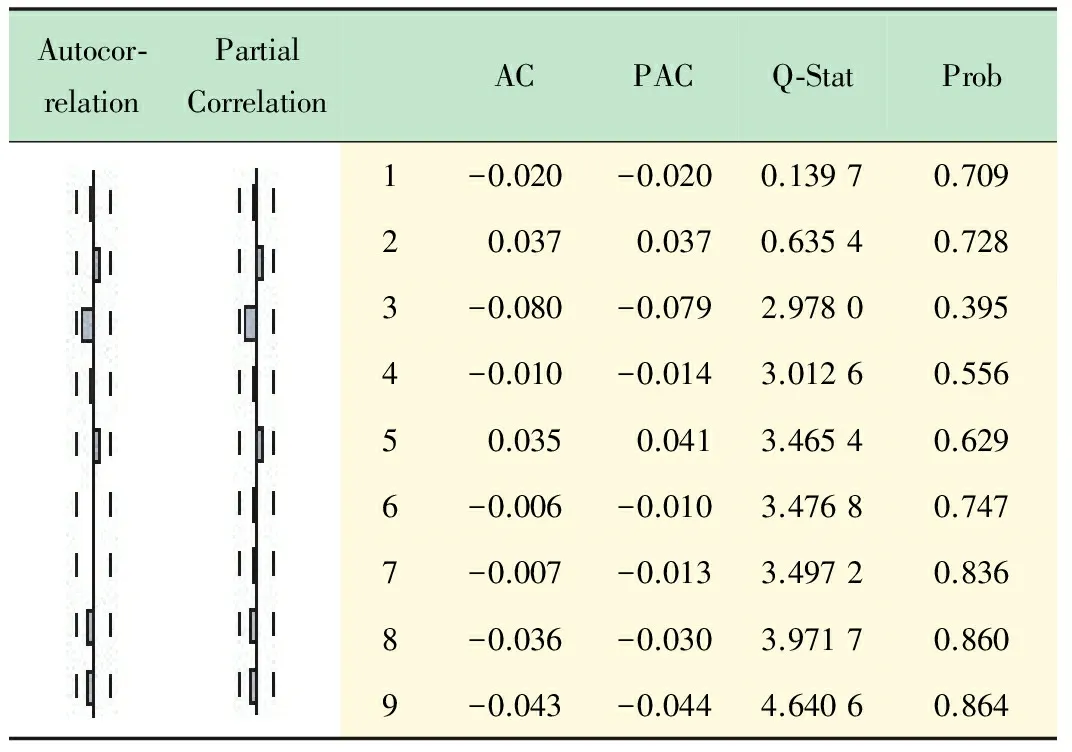
3 結(jié) 語


