定積分的定義及其應用
唐方旭
(天津財經大學珠江學院基礎課部,天津,301811)
一、引言
定積分起源于求圖形的面積和體積等實際問題。古希臘的阿基米德用“窮竭法”,我國的劉徽用“割圓術”,都曾計算過一些幾何體的面積和體積,這些均為定積分的雛形。直到17世紀中葉,牛頓和萊布尼茨先后提出了定積分的概念,并發現了積分與微分之間的內在聯系,給出了計算定積分的一般方法,方使定積分成為解決有關實際問題的有力工具,并使各自獨立的微分學與積分學聯系起來,構成完整的理論體系——微積分學。
二、定積分的定義
定義1[1]設函數f(x)在區間[a,b]上有定義,用(a,b)內的n-1個分點
a=x0 故Dirichlet函數在[0,1]上不可積。 例3 何時有λ→0?n→∞? 利用此公式可以計算一類極限問題。 定義2[2]設函數f(x)在區間[a,b]上有定義,將[a,b]區間進行n等分 利用定積分定義求解一類極限問題。 理論依據:設函數f(x)在區間[0,1]上可積分,則 實例分析: 分析:將這類問題轉化為定積分主要是確定被積函數和積分上下限。若對題目中被積函數難以想到,可采取如下方法:先對區間[0,1]n等分寫出積分和,再與所求極限相比較來找出被積函數與積分上下限。 例4[4]極限 =________ 例5 求極限 [1] 盧興江,金蒙偉.微積分[M].杭州:浙江大學出版社,2012. [2] 柳潔冰,張宏亮.關于定積分定義及可積條件的討論[J].科教文匯:上旬刊,2011(3). [3] 陳仲.高等數學競賽題解析教程[M].南京:東南大學出版社,2010. [4] 田勇.碩士研究生入學考試歷年真題解析:理工數學二[M].北京:機械工業出版社,2002. [5] 張瑜.21世紀高職高專課程改革新教材:高等數學競賽教程[M].蘇州:蘇州大學出版社,2009.









三、定積分定義的應用
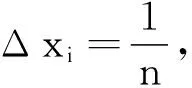



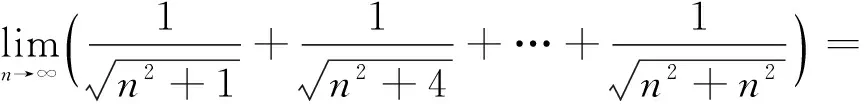


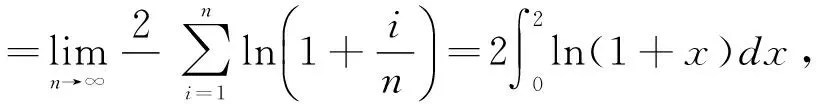




四、小結


