順學而教,在“存異”中“求同”
——以解決問題的策略(假設)為例
楊金珠
(南京市江寧實驗小學,江蘇南京,211106)
蘇教版六(上)解決問題的策略(假設)是在學生已經學習了畫圖、列表、一一列舉和倒推等策略基礎上又一次有關策略的學習,許多課外輔導用書和提優訓練都把此類問題稱之為“雞兔同籠”。解決此類問題需要學生具備較高的思維水平和邏輯推理能力。
一、了解學生學習情況
為了全面掌握學生知識情況,筆者課前對所教兩個班級103名學生進行“學習前置”(只做“自主探索”部分)。
表1學生預習表

課題解決問題的策略(2)自主探索 例2:全班42人去公園劃船,一共租了10只船。每只大船坐5人,每只小船坐3人。租用的大船和小船各有多少只?想一想:你能用已學過的策略解決這個問題嗎?
結果統計如表2。

表2 學生預習情況統計
從上表信息可知:學生想到用列表方法(含多種方法中的列表)解決的有50人,占49%;畫圖9人,占8.7%;算式54人,占52.4%;方程14人,占13.6%。通過分析能看出學生解決此類問題時所使用的一般方法是列表法和假設法。接著,筆者對學生做了進一步調查。
師:你是怎么想到用這些方法的?
生1:我們在五年級學過一一列舉,這道題目數字不大,我一個一個列出來就能找到答案了。
生2:畫圖的方法比較直觀,好理解。
生3:這學期第一單元我們學的就是方程,根據等量關系就可以列出方程,不過怎樣解方程是我爸爸教的。
生4:我在輔導班的時候學過用假設法求解。
師:對于用假設法列出的算式你能解釋每一步表示的意義嗎?
生4:我只是記住算式模型。
通過訪談,可以較客觀地了解到學生對于此類問題的一般思考過程和個體間的思維差異。教學中要尊重這種差異,充分展示彼此間不同的觀點和想法,在多維立體互動中不斷對學生差異進行比較、修正和提升。而這,無疑是需要教師進行思考和正視的。
二、教學案例分析
(一)列表
1.陳諾:我先從9只大船1只小船開始想。9只大船1只小船可以坐50人,比42人多,8只大船2只小船……
生1:當我們列舉出“6只大船4只小船”正好坐42人時,下面就不要再列舉了。因為隨著大船的增加,小船的減少,人數會越來越多,肯定不符合條件。
師:對于這張表格的數據同學們有什么發現?
生2:每增加1只大船,減少1只小船,人數會多2人。
生3:我補充一下,應該有個條件“船的只數10只”要保持不變。
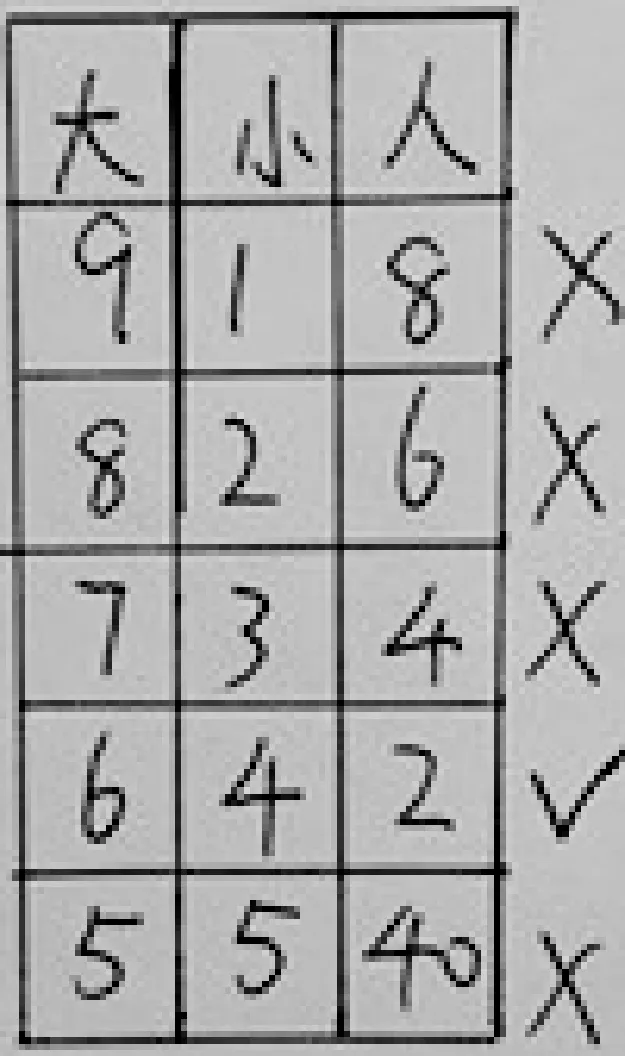
一一列舉是學生以前學過的策略,這其中就蘊含了“假設”的思想,學生通過同學對列表方法的介紹,初步體會“假設”思想在列表中的運用。同時,與以前所學的一一列舉答案的多樣性不同,此類題目答案是唯一的。
師:我覺得應該從“10只大船0只小船”開始想。雖然“10只大船和0只小船”一看就知道不符合條件,但如果寫出來的話,這樣列表就會很有序。
(用紅筆補上“10只大船0只小船”)
假設策略的重心是假設后的調整,調整的過程實質上是替換的過程。在“一一列舉”中其實就蘊含“一一替換(1只小船替換1只大船)”的思想。當教師提出需要補上“10只大船0只小船”時,“10大0小”或“0大10小”正是下面學生畫圖、假設法的基礎,這樣從學生熟知的列表法切入符合學生的實際。
2.唐沛年:我和陳諾的方法有點不一樣,我是從1只大船9只小船開始想的……

生1:我發現陳諾列舉的次數多。
師:你能解釋其中的原因嗎?
生1:當我們假設9只大船1只小船時,總人數是48人,48離42很近。而1只大船和9只小船總人數是32人,離42比較遠。
生2:有價值的發現!如果從不同的角度思考,替換次數會有不同。
生3:應該像陳諾那樣補上“0只大船和10只小船”的情況。
設計意圖:學生兩種不同的列表方法實際上就是兩種不同假設法的原型。在這里通過師生對話、生生互動,為下面調整假設策略解決問題做了提前滲透和有力鋪墊,可謂“未成曲調先有情”。
3.岳晨曦:我先假設有5只大船和5只小船,可以坐40人,然后4只大船6只小船發現人數少得更多,所以應該是6只大船4只小船。
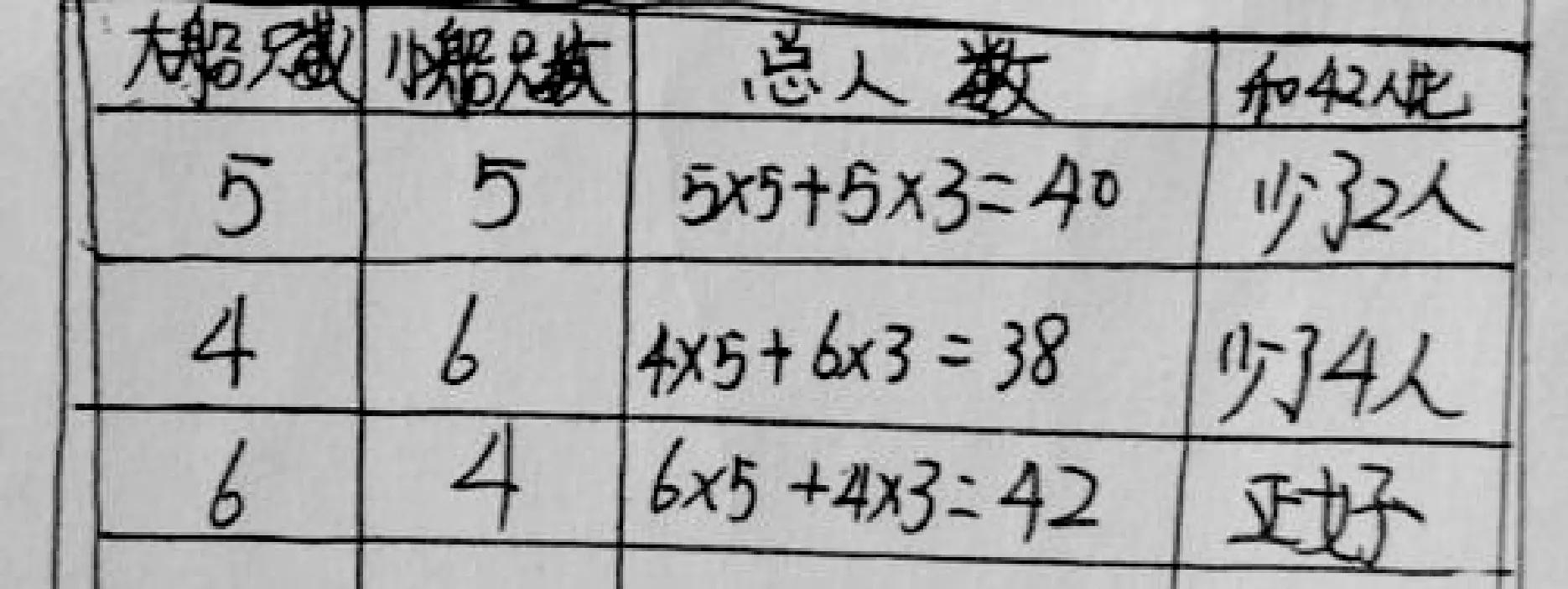
師:是的,當岳晨曦先假設“5大5小”時發現和42人是有“差距”的,岳晨曦先用向小船方向調整,發現人數少更多,所以才向大船方向調整,誰能解釋其中的道理?
一股透骨的寒氣直抵他的心底里,他不禁打了一個寒顫。莫非……他不敢繼續想下去了,那簡直太可怕了!還沒有弄清事實的真相,一股巨大的憂郁就將他徹底地擊傷了,他默不作聲,離開了茶莊。山野中移動著一個越來越小的灰點,像一朵灰暗的流云在緩慢地往山坡下飄移。冷颼颼地刮來一陣涼風,他突然感到滿目瘡痍的荒涼,身子也失重似的飄浮起來。以往,他喜歡獨來獨往,喜歡獨自在山野里漫步,享受那份清靜,那種自在,孤獨與快樂。可是眼下,他像一個幽靈似的在荒山野嶺里飄蕩著,紅塵世界里,他只能是一只小小的螻蟻。佛在云端拈花微笑,是否見到了他這枚枯黃的落葉在風中飄動?
生:當5只大船5只小船時坐40人,比42人少,所以應該增加大船減少小船,因為大船能坐更多的人。
設計意圖:調整可以是“漸進式”的,也可以是“跨越式”的,無論從哪個角度想起,重點都是要讓學生借助表格感受為什么要把大船換成小船或者為什么要把小船換成大船,以及因為“換”而帶來的人數變化。充分展開這個過程,使學生深刻體會調整的目的、方向和方法,進而初步形成調整意識。
(二)畫圖
陶致遠講解畫圖過程。

師:陶致遠為什么一次只畫去2人?
生:一只小船替換一只大船只能少2人。
師:誰能把陶致遠和陳諾的方法聯系來說一說?
設計意圖:借助圖示,結合學生的講解把結果的呈現過程化、動態化,清晰呈現畫圖過程。并與列表方法相互比較,相互驗證,相互啟迪。這其中算式方法的雛形已初見端倪,使學生對假設策略的認識進一步接近其核心和本質。
(三)算式
蔣霏凡介紹自己的思考過程。
師:同學們,“數形結合”是一種重要的思想方法,你能不能根據陶致遠的“圖”來解釋這位同學的算式呢?

設計意圖:細細分析列表、畫圖和算式,可以發現都有假設和替換的影子。某些時候,它們的思路完全一致。“打通”這些方法的聯系,讓學生通過不同的方式理解同一種策略,理解會更深刻。
師:明明假設的全是大船,怎么求出來的卻是小船呢?
(學生一時難以回答,沉默片刻后,從畫圖方法中找到了解釋)
生1:因為假設全是大船,會多算出8人。
生2:把多算的8人要“趕下船”,1只大船“趕”下兩人后就變成小船,因為要“趕”4次,就變成了小船。所以假設全是大船,求出來的就是小船。
生3:如果假設全是小船,求出來的就是大船。
設計意圖:為什么明明假設的是大船,求出來的卻是小船?這歷來是不少學生的困惑之處。在這里,教師應放大這個環節,在反問、追問中,放慢進程,借助表格的直觀、示意圖的支撐、形成式的凝練,理解掌握假設法的內涵和本質,在此基礎上抽象出一般算式方法。
三、分析總結
通過列表和畫圖不難發現,隨著小船數量的逐一增加,總人數逐次減少2人,正是這一基本的變化規律,我們很容易得出“如果人數要減少2人,應該將一只大船‘變成’小船,反之,人數要增加2人,應該將1只小船‘變成’1只大船”。進而思考:如果人數要減少8人(增加12人),應該將幾只大船(小船)“變成”幾只小船(大船)?有了這些觀察思考的基礎,在列表和畫圖中就找到了“假設法”的影子。如果說第一次列舉被視為假設的前提,那么接下來就可以根據人數的差距,計算出應該將多少只大船(小船)“變成”小船(大船),就能解決一共有多少只大船和多少只小船的問題。由此,解決“雞兔同籠”一類問題的典型方法——假設法,便躍然紙上。這樣教學不僅切合教材的實際,而且切合教學的實際,更是切合學生的實際。
[1] 周勝瓊.小學數學六年級上冊“雞兔同籠”教學反思[J].中國科教創新導刊,2012(6).
[2] 潘粉娥.“雞兔同籠問題”教學設計[J].課程教材教學研究:小教研究,2013(12).
[3] 王興.淺談如何提高小學六年級數學的教學質量[J].教育教學論壇,2013(11).

