雙向飛翼超聲速客機激波阻力和聲爆研究

李占科, 張旭, 馮曉強, 關曉輝

(西北工業大學 航空學院,陜西 西安 710072)

雖然以“協和號”為代表的超聲速客機由于各種原因而退出歷史舞臺,但是人們超聲速旅行的需求和夢想卻沒有因此而中斷和停止,歐美等國一直在致力于新一代超聲速客機的研究[1]。如美國波音公司的“靜音超聲速計劃(QSP)”,洛馬公司的“安靜超聲速客機(QSST)”,俄羅斯圖波列夫設計局的“圖-244”,英國的“A-2”等。由于“協和號”退出運營的主要原因是經濟性差和噪聲污染,因此新一代超聲速客機項目的研究以提高氣動效率和減少噪聲(主要是聲爆)為重點內容[2]。

影響超聲速客機氣動效率的首要因素是超聲速飛行時由強激波造成的激波阻力, 降低超聲速巡航時的激波阻力對于超聲速客機具有十分重要的意義。聲爆是超聲速飛機產生激波并傳播到地面形成的[3],它關系到超聲速客機能否被允許在陸地上空飛行,是最需要解決的超聲速客機噪聲問題。若效率和噪聲問題得不到解決,超聲速飛機就不會實現經濟和環保。

雙向飛翼的概念由邁阿密大學査葛城教授提出[4-6]。雙向飛翼超聲速客機以大展弦比狀態起飛著陸,通過飛行方向轉變,以小展弦比狀態進行超聲速巡航。這樣就解決了起飛著陸狀態和超聲速巡航狀態飛行器外形要求相互矛盾的問題。

為了使雙向飛翼超聲速客機產生的地面聲爆信號盡可能小,査葛城教授提議使用下表面更為平坦的翼型來構成雙向飛翼。平坦的下表面減小了飛翼對下表面超聲速氣流的擾動,可以降低向飛行器下方傳播的激波強度,從而達到降低聲爆的目的。

本文將基于雙向飛翼構型,以CFD方法進行阻力計算,以F-BOOM程序進行聲爆計算,研究翼型、平面形狀和EFCE激波阻力優化算法對雙向飛翼激波阻力和聲爆的影響,形成對雙向飛翼構型低阻力設計和低聲爆設計的權衡研究。

1 計算方法與網格的選取

1.1 計算方法

本文以雙向飛翼構型為基礎,利用CFD方法進一步的探討該構型的阻力和聲爆特性。由于本文討論對象為超聲速情況下的激波阻力,所以暫不考慮激波對于附面層的干擾以及氣體黏性帶來的阻力。因此,求解歐拉方程即可滿足精度要求,笛卡爾坐標系下的歐拉方程方程如公式(1)～(4)[7-8]。

(1)

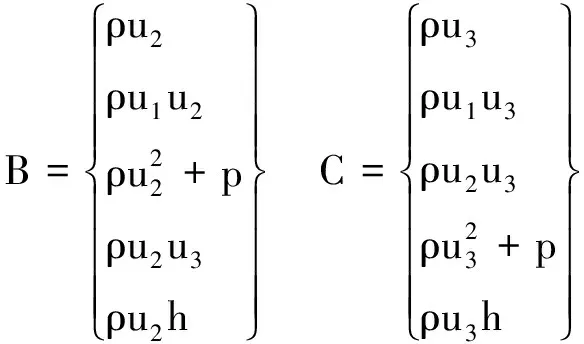
(2)

式中：u1、u2、u3分別為為笛卡爾坐標系x、y、z方向上的速度,ρ為密度,P為壓力,E代表氣體的總能量,壓力及總能量之間的關系如公式(3)所示,h的表達式如公式(4)所示

(3)

(4)

文獻[9]進行了超聲速客機低聲爆布局設計及聲爆預測算法方面的研究,開發了F-BOOM程序,利用CFD計算提供的近場超壓值,可推算出地面遠場的聲爆信號,是聲爆計算領域的重要方法。

F-BOOM所用的方法是一種基于CFD和波形參數法的遠近場耦合匹配的高精度聲爆預測方法[10]。主要通過CFD對飛機近場擾動進行求解,利用得到的近場壓力分布,通過波形參數法求解遠場壓力擾動。

通過求解歐拉方程得到近場壓力分布,計算結果經過匹配之后用于遠場聲爆的計算。公式(5)～公式(7)為遠場波動方程[11],通過輸入近場的壓力擾動可以計算得到遠場的聲爆信號。

(5)

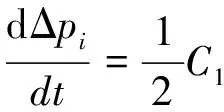
綜上所述，齊齊哈爾大學圖書館開展閱讀推廣活動對大學生的品德教育是有一定影響的，也在開展閱讀推廣活動的同時總結經驗、完善不足，也希望高校圖書館的閱讀推廣活動能夠更有深度和廣度，但是圖書館的閱讀推廣仍然處于初期階段，仍需要和其他高校圖書館進行溝通和合作，促進高校圖書館的閱讀推廣活動能夠上一個臺階，讓學生能夠切身去感受品德的重要性。

(6)

(7)

式中:第i段聲爆信號的持續時間為λi=Ti+1-Ti,壓強隨時間的變化率為mi=(pi-pi-1)/λi,通過激波后的壓強增量為Δpi=pi-pi-1。

1.2 計算網格的選取

本文計算是在半機身模型上進行的,使用網格為結構六面體網格,網格密度為238×90×94,總網格量為200萬左右,如圖1a)所示。整個網格區域包括流場區域和半翼身組合體,外邊界條件設定為壓力遠場。圖1b)為模型周圍網格分布放大圖,為保證計算結果的精確度,越靠近模型壁面,網格劃分越密集,并對模型重點區域的網格進行了加密。

聲爆近場精確預測的關鍵在于能否對近場的激波進行精確捕捉和計算。因為激波在傳播過程中主要沿馬赫面方向,所以為了更精確地捕捉激波及擾動,本文采用楔形網格[12],即網格以馬赫角為斜度傾斜。本文采用2.0馬赫所對應的60°馬赫角為傾斜角。

圖1 流場網格

2 雙向飛翼激波阻力和聲爆研究

2.1 翼型對雙向飛翼激波阻力和聲爆的影響

本節研究翼型對雙向飛翼激波阻力和聲爆的影響。所使用的超聲速雙向飛翼構型的巡航馬赫數為2.0。模型平面形狀如圖2所示。超聲速巡航狀態下的內側機翼后掠角78°,外側機翼的后掠角為46°,其展弦比為1.53;亞聲速狀態下的內側機翼后掠角44°,外側機翼的后掠角12°,其展弦比為6.18。

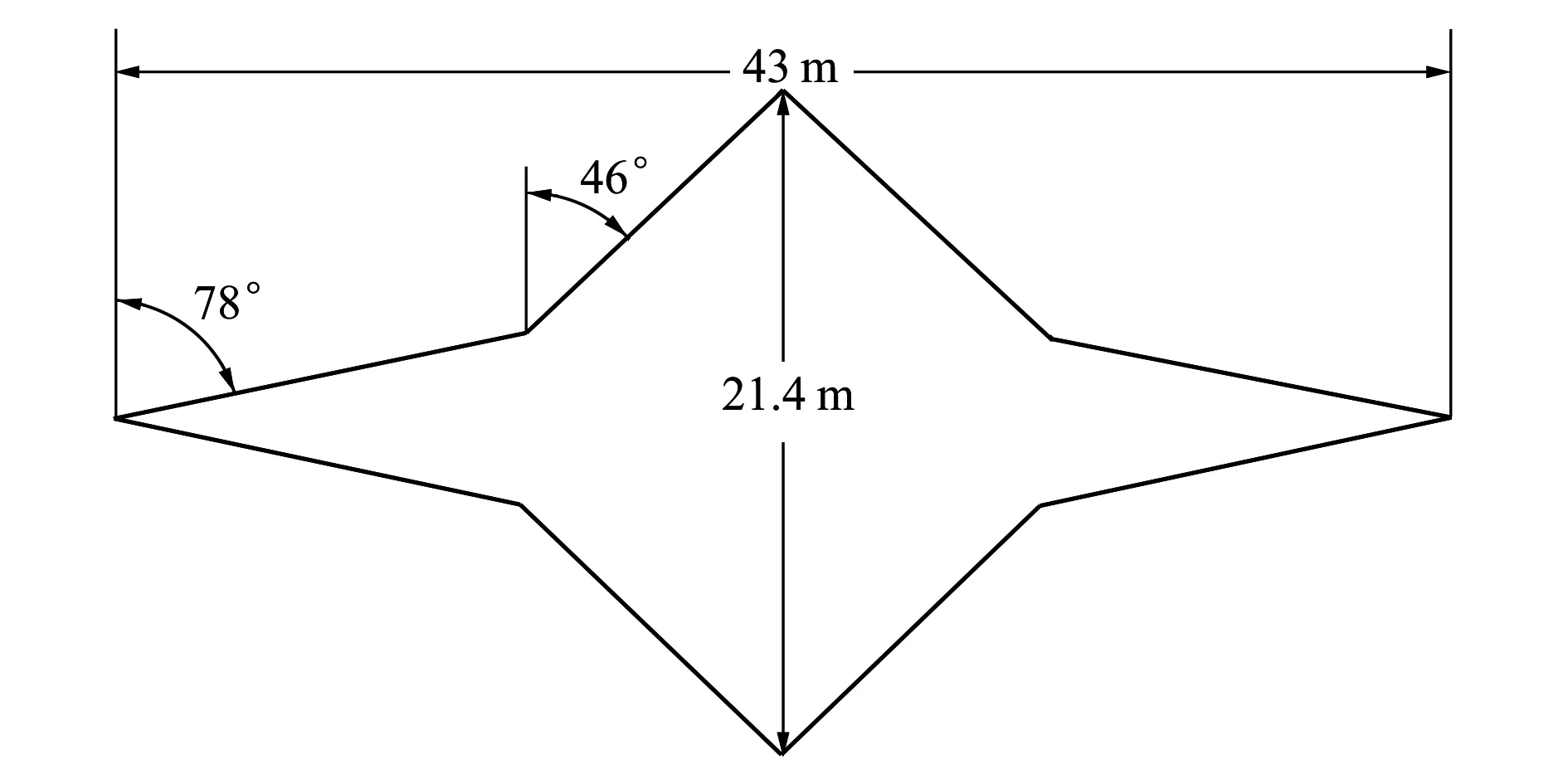
圖2 平面形狀

本節首先將從激波阻力方面對平底翼型和雙圓弧對稱翼型構成的雙向飛翼構型進行考察。依據《飛機設計手冊》中關于民用飛機客艙高度的規定[13],采用相對厚度為6%的構型。保持飛翼的相對厚度不變,分別使用平底翼型和雙圓弧對稱翼型構成雙向飛翼外形,其中平底翼型的上表面曲線高度是對稱翼型上表面曲線高度的2倍。圖3為2種翼型構成的飛翼在來流馬赫數為2.0的情況下求解歐拉方程得到的10°迎角以內的極曲線對比,其中阻力包括激波阻力和升至渦阻力,即壓差阻力,不考慮摩擦阻力。

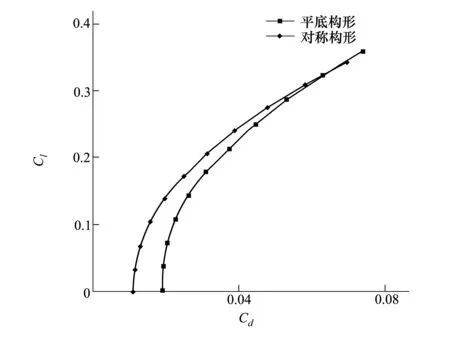
圖3 小迎角狀態下極曲線對比

從圖3可以看出由對稱翼型構成的雙向飛翼構型在小迎角狀態下的阻力系數明顯小于由平底翼型構成的雙向飛翼構型。隨著迎角的增大,二者的阻力系數的差別逐漸縮小,但在10°迎角以內仍然是對稱構型的阻力系數小于平底構型的阻力系數。從圖3中可以看出小迎角下對稱構型的升力系數只略小于平底構型的升力系數,二者差別很小,但是隨著迎角的增大,升力系數差別逐漸增大。在10°迎角下平底構型的升力系數明顯大于對稱構型的升力系數。由于超聲速巡航一般是在小迎角狀態下進行的,從升阻特性的角度來看,對稱翼型構成的雙向飛翼構型作為超聲速客機的氣動外形更加有利。

如圖4所示,為由平底翼型和對稱翼型組成的雙向飛翼構型在馬赫數為2.0時,0°迎角下求解歐拉方程得到的上表面壓強分布對比。從圖中可以看出,平底構型的前緣激波與后緣膨脹波的強度和范圍都大于對稱構型,這是導致其阻力系數大于對稱構型主要原因。在保持飛翼相對厚度相同的情況下,平底構型飛翼的上翼面高度將是對稱構型的2倍,這雖然使平底構型的下表面對來流的擾動減小了,但卻使其上表面對氣流的擾動大大增強,產生更強的激波和膨脹波,反而比上下表面都產生較弱的激波與膨脹波的上下對稱構型產生更大的阻力。

圖4 壓強對比

采用F-BOOM方法分別對0°迎角時2種雙向飛翼構型進行聲爆計算,結果見圖5。圖中的超壓部分顯示了超聲速雙向飛翼構型在0°迎角、反射因子1.9時地面的N形波聲爆特征。從圖中可以看到,對稱構型的遠場超壓值為38.25 Pa,遠遠高于平底構型的22.15 Pa,噪聲級別較高。

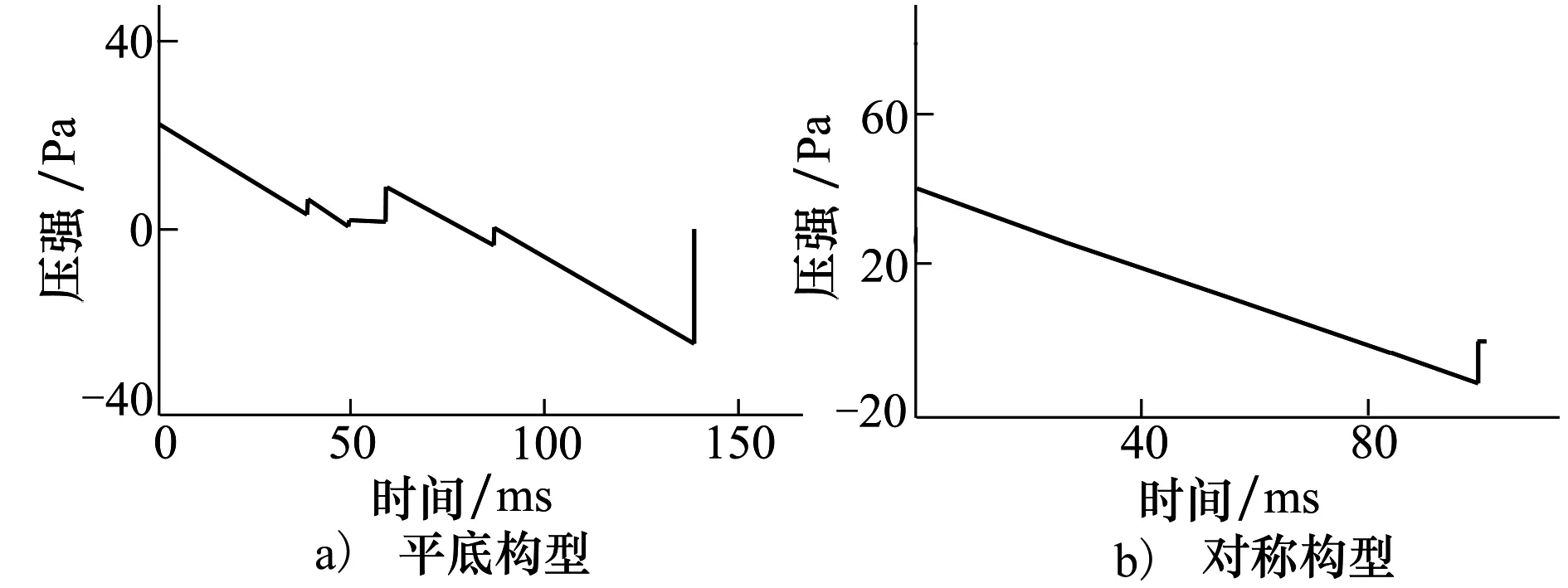
圖5 聲爆計算結果

平底翼型可以明顯降低機翼下表面的激波強度,進而降低雙向飛翼超聲速客機的超聲速巡航的聲爆,卻很大程度上增加了巡航阻力;對稱翼型在減小激波阻力方面有其固有優勢,卻增加了機翼下表面的激波強度,提高了聲爆。可見在實際設計中需要進行相關的權衡研究。

2.2 平面形狀對雙向飛翼激波阻力和聲爆的影響

本節研究平面形狀對雙向飛翼激波阻力和聲爆的影響。所使用的超聲速雙向飛翼構型采用長60 m,寬21.4 m,相對厚度4.3%的設計,與前一節所用構型的客艙高度保持一致,平面形狀變化如圖6所示。超聲速巡航狀態下的內側機翼后掠角81°,外側機翼的后掠角為58°,其展弦比為1.19;亞聲速狀態下的內側機翼后掠角32°,外側機翼的后掠角9°,其展弦比為9。根據所使用翼型的不同,仍然分為平底構型和對稱構型。

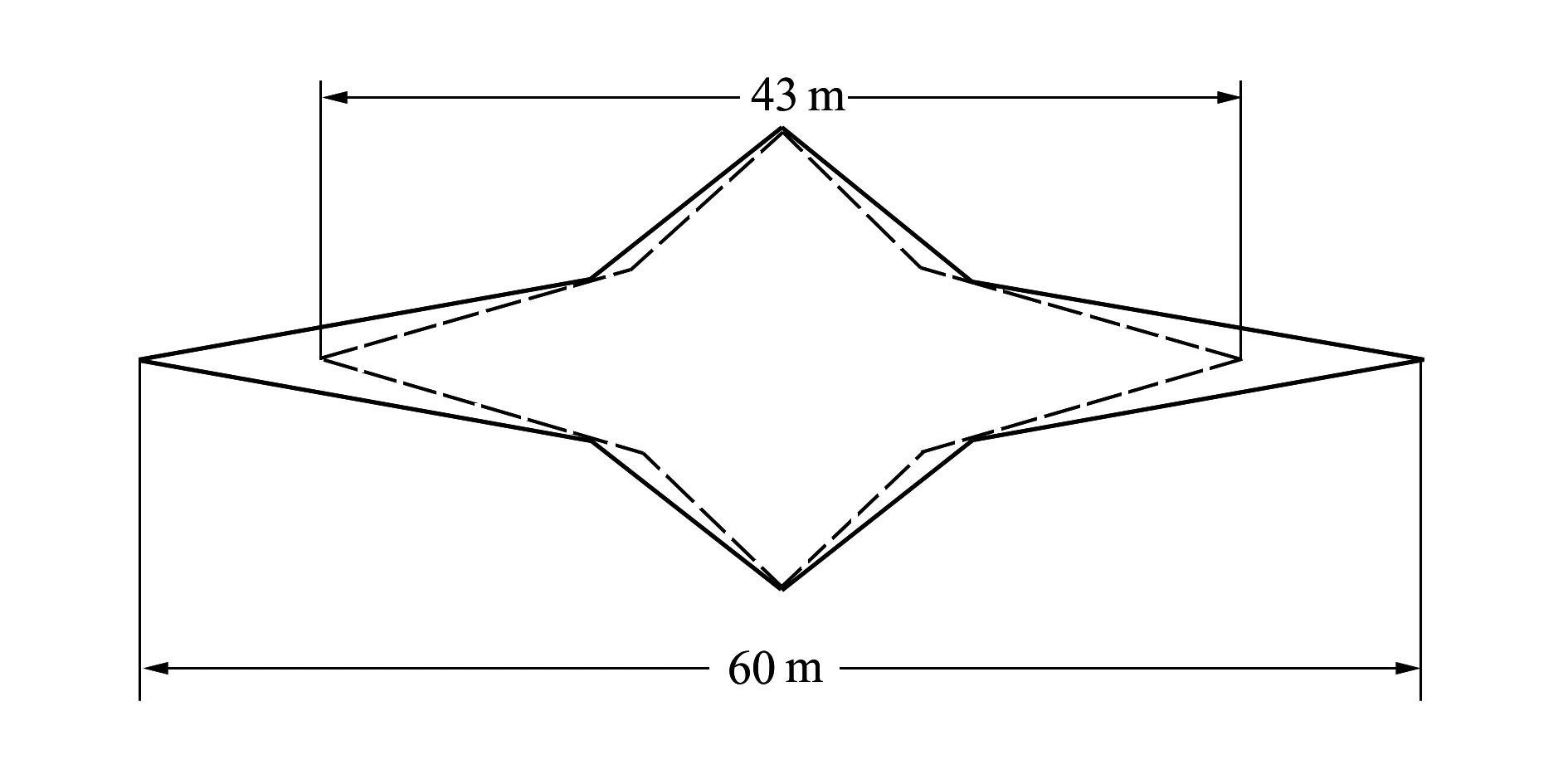
圖6 平面形狀變化示意

對2種構型的模型分別建立網格后,進行CFD計算,求解歐拉方程得到各模型0°迎角時的阻力系數。圖7是其各自的壓力云圖。

圖7 壓力云圖

采用F-BOOM程序,對3種模型0°迎角時的聲爆水平進行計算,得到2種構型在0°迎角、反射因子1.9時地面的N形波聲爆特征(見圖8)。具體計算結果見表1。

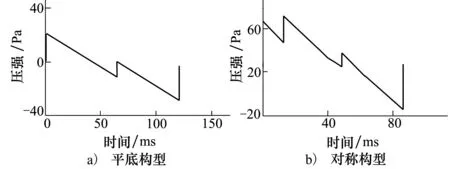
圖8 聲爆計算結果

從表中的數據可以看到,阻力方面,與較短的構型相比,不管是平底構型還是對稱構型,其對應較長構型的阻力系數都有了大幅下降。其中平底構型的阻力系數下降了52.36%,對稱構型的阻力系數下降了65.22%。

表1 計算結果

聲爆方面,較長的平底構型比較短的平底構型稍有下降,幅度為8.8%。而對稱構型的聲爆水平則有36.25%的大幅下降,達到24.4 Pa。表明在聲爆方面,幾何外形對于對稱構型的影響更為明顯。然而,對稱構型的聲爆水平仍高于平底構型。

從以上研究結果可以得出結論,細長的平面幾何形狀對2種構型雙向飛翼的低阻力設計都非常有利,對降低聲爆也有作用,尤其對降低對稱構型的聲爆效果明顯。

2.3 EFCE激波阻力優化算法對雙向飛翼激波阻力和聲爆的影響

文獻[14]提出了擴展的遠場組元(extended far-field composite element,EFCE)翼身組合體激波阻力優化算法,可以對超聲速翼身組合體進行零升激波阻力優化。EFCE激波阻力優化方法使用超聲速面積率進行激波阻力計算,結合拉格朗日乘子法進行優化參數的計算,無須迭代,是超聲速飛行器概念設計階段降低機翼機身激波阻力的一種有用的氣動外形優化方法,對超聲速細長體外形飛行器的氣動外形設計有一定的參考價值。

本節采用EFCE方法對60 m長的對稱構型雙向飛翼進行激波阻力優化。EFCE方法使用CST參數化方法[15]對機翼外形進行參數化表示(見圖9),以零升激波阻力最小為目標對雙向飛翼進行厚度分布優化。

圖9 雙向飛翼外形的CST表示

對優化后的模型進行0°迎角下的阻力和聲爆計算,結果見表2。

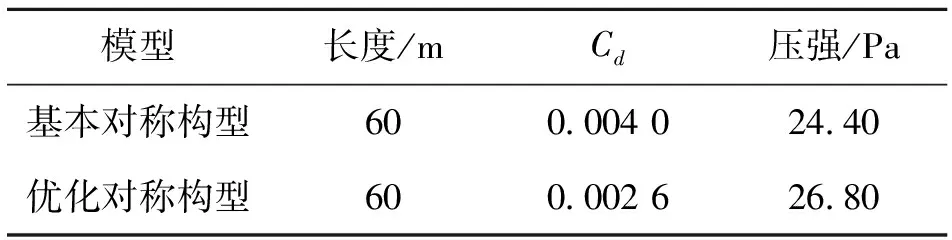
表2 優化結果

從計算結果可以看出,經過優化后模型的阻力系數下降了35%。但同時可以看到,優化后模型的聲爆水平有略微的提高。

為了進一步研究,本節對平底構型、對稱構型和EFCE方法優化過的對稱構型在0°到3°迎角下的聲爆水平進行了計算,對比情況見圖10。通過曲線可以看到,對雙向飛翼激波阻力的優化確實會帶來聲爆方面的不利影響,而且隨迎角的增加呈擴大趨勢。這是因為對雙向飛翼的激波阻力進行優化的時候改變了機身機翼的厚度分布,進而對聲爆水平產生影響。

圖10 3種構型聲爆對比

因此,在應用EFCE優化算法或其它優化算法時,應進行全面考慮。

3 結論

1) 雙向飛翼的平底構型雖然能夠降低超聲速巡航時飛行器下表面向下傳播的激波強度,從而降低聲爆信號,但與同等容積的上下對稱構型相比卻大幅增加了超聲速巡航的激波阻力。

2) 細長的平面幾何形狀對兩種構型雙向飛翼的低阻力設計都非常有利,對降低聲爆也有作用,尤其對降低對稱構型的聲爆效果明顯。

3) 遠場組元(far-field composite element,EFCE)翼身組合體激波阻力優化算法對雙向飛翼構型減小波阻有明顯效果,但同時會略微提高該構型的聲爆信號。

因此,在超聲速客機研究中,要根據具體設計需求對超聲速客機的減阻設計和低聲爆設計進行權衡處理。

參考文獻：

[1] National Research Council. High Speed Research Aeronautics and Space Engineering Board U.S. Supersonic Commercial Aircraft: Assessing NASA′s High Speed Research Program[M]. Washington, D.C. National Academy Press,1997

[2] 馮曉強,宋筆鋒,李占科. 超音速客機音爆問題初步研究[J]. 飛行力學, 2010, 28(6): 21-23

Feng X Q, Li Z K, Song B F. Preliminary Analysis on the Sonic Boom of Supersonic Aircraft[J]. Flight Dynamics, 2010, 28(6): 21-25 (in Chinese)

[3] 楊訓仁,陳宇. 大氣聲學[M]. 北京：科學出版社, 2007: 256-260

Yang X R, Chen Y. Atmospheric Acoustics[M]. Beijing: Science Press, 2007: 256-260 (in Chinese)

[4] Zha G C. Toward Zero Sonic-Boom and High Efficiency Supersonic UAS: A Novel Concept of Supersonic Bi-Directional Flying Wing. U S Air Force Academic Outreach UAS Symposium,Grand Forks, ND, 2009

[5] Zha G C, Im H, Espinal D. Toward Zero Sonic-Boom and High Efficiency Supersonic Flight,Part I: A Novel Concept of Supersonic Bi-Directional Flying Wing[R]. AIAA-2010-1013

[6] Zha G C, Im H, Espinal D. Supersonic Bi-Directional Flying Wing, Part II: Conceptual Design of a High Speed Civil Transport[R]. AIAA-2010-1393

[7] 李鳳蔚. 空氣與氣體動力學引論[M]. 西安：西北工業大學出版社,2007

Li F W. Introduction of Aerodynamics[M]. Xi′an, Northwestern Polytechnical University Press, 2007 (in Chinese)

[8] Siclari M. CFD Predictions of the Near-Field Sonic Boom Environment for Two Low Boom HSCT Configurations[R]. AIAA-1991-1631

[9] 馮曉強,宋筆鋒,李占科等. 超聲速飛機低聲爆布局混合優化方法研究[J]. 航空學報, 2012, 34(8): 1768-1777

Feng X Q, Song B F, Li Z K, et al. Timized Approach for Low Boom Supersonic Aircraft Configuration[J]. Acta Aeronautica et Astronautica Sinica, 2012, 34(8): 1768-1777 (in Chinese)

[10] Siclari M, Darden C. A Euler Code Prediction of Near to Mid-Field Sonic Boom Pressure Signature[R]. AIAA-1990-4000

[11] Thomas C L. Extrapolation of Sonic Boom Pressure Signatures by the Waveform Parameter Method[R]. NASA TND-6832

[12] 馮曉強. 聲爆計算方法研究及在超聲速客機設計的應用[D]. 西安：西北工業大學, 2012: 43-53

Feng X Q. The Research of Sonic Boom Prediction Method and Application in Supersonic Aircraft Design[D]. Xi′an, Northwestern Polytechnical University, 2012: 43-53 (in Chinese)

[13] 飛機設計手冊總編委. 飛機設計手冊(第5冊) [M]. 北京: 航空工業出版社, 2002: 11-12

Aircraft Design Manual (Volume 5)[M]. Beijing: Aviation Industry Press, 2002: 11-12 (in Chinese)

[14] 關曉輝,宋筆鋒,李占科. 超聲速翼身組合體激波阻力優化的EFCE算法[J]. 航空學報, 2013,34(5): 1036-1045

Guan X H, Song B F, Li Z K. Extended Far-Field Composite Element Supersonic Wing-Body Wave Drag Optimization Method[J]. Acta Aeronauticaet Astronautica Sinica, 2013, 34(5): 1036-1045 (in Chinese)

[15] 關曉輝,李占科,宋筆鋒. CST氣動外形參數化方法研究[J]. 航空學報, 2012, 33(4): 625-633

Guan X H, Li Z K, Song B F. A Study on CST Aerodynamic Shape Parameterization Method[J]. Acta Aeronauticaet Astronautica Sinica, 2012, 33(4): 625-633 (in Chinese)