凸肩葉片抗共振的模糊可靠性評估方法

張萌, 陸山

(西北工業大學 動力與能源學院, 陜西 西安 710072)

葉片是航空發動機的主要部件之一,由于共振引起的葉片故障往往占發動機零件疲勞故障的30%～40%,研究葉片的抗共振可靠性具有重要意義。葉片振動過程中含有大量的模糊因素[1]，主要有2大類:①振動失效區域的模糊性；②基本變量的模糊性。考慮前者的可靠性模型稱為基于狀態模糊性的振動可靠性模型;考慮后者的可靠性模型稱為基于變量模糊性的振動可靠性模型。目前關于構件抗共振的模糊可靠性研究成果較少,且均為基于狀態模糊性的振動可靠性研究[2-4]。這些研究都只考慮了共振失效域的模糊性,而忽略了振動固有頻率的模糊性。因此,本文將分析帶阻尼結構(如凸肩)葉片固有頻率的客觀模糊性,建立基于變量模糊性的葉片抗共振模糊可靠度模型。

1 帶阻尼結構葉片固有頻率的模糊性

帶阻尼結構葉片固有頻率的模糊性主要源于:

1) 帶阻尼結構(如凸肩)葉片的固有頻率受到眾多因素的影響,其中有些因素對固有頻率的影響比較復雜,還有些因素(如凸肩相對榫齒周向位置偏移,榫頭榫槽安裝緊度等)對固有頻率的影響尚無規律可言,甚至存在某些未知的偶然因素也會對其產生影響,這使得帶阻尼結構葉片的固有頻率本身具有模糊性;

2) 固有頻率的獲取過程具有模糊性,試驗方案的制定、試驗裝置或者算法和程序的設計等,都依賴試驗人員的經驗和主觀意識,而經驗和意識本身就是模糊的；此外,設備的完備程度、穩定程度(如帶凸肩平板葉片固有特性試驗時,接觸壓力在振動過程中本身就是變化的,因而測不準[5])等,也帶有一定的模糊性。

可見，只從隨機的角度來解釋固有頻率是不夠的，還應引入模糊理論對常規方法進行補充和修正。

2 模糊性的描述

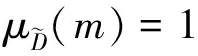
步驟1 確定固有頻率中值m

1) 確定統計區間[TL,TU];其中下限TL應比數據最小值略小,而上限TU應比數據最大值略大;

2) 給定分組數k,計算組距l并分組;分組區間為[si,si+1](i=1,…,k),其中si=TL+l(i-1);

3) 統計落在各分組區間內的數據個數Ni,并求出Nmax=max(N1,N2,…,Nk);

4) 判斷:若Nmax=Nj(j∈{1,…,k})且j值唯一,則為有效分組,此時以分組區間[sj,sj+1]的組中值mj=(sj+sj+1)/2作為固有頻率中值,即令m=mj;若j值不唯一,則為無效分組,此時應改變分組數,重復步驟2～步驟4,直至分組有效。

步驟2 確定各分組區間組中值及其隸屬度

計算各分組區間[si,si+1](i=1,…,k)組中值mi,取Di=Ni/Nj為mi的隸屬度,則得數據點列(mi,Di)(i=1,…,k);

步驟3 處理數據,擬合隸屬函數

1) 對(mi,Di)(i=1,…,k)進行處理;刪去隸屬度為0的中間數據,即:若Di=0,并存在ri且Dr≠0,Ds≠0,則刪去(mi,Di)。處理后得新的數據列(mij,Dij)(j=1,…,p)且p≤k;

2) 以數據(mj,1)為分界點,對數據點列(mij,Dij)(ij≤j)在約束L(mj)=1下進行擬合,得到L(x);對數據點列(mij,Dij)(ij≥j)在約束R(mj)=1下進行擬合,得到R(x);

步驟4 隸屬函數性質檢驗與改寫

對擬合出的函數L(x)和R(x)進行性質檢驗,確保L(x)和R(x)滿足單點L-R型隸屬函數的定義。若其值域可取負值,則應對其進行非負截斷改寫,即:若L(x1)=0,則定義x≤x1時,L(x)≡0;若R(x2)=0,則定義x≥x2時,R(x)≡0。

至此,中值m、函數L(x)和R(x)均已得到,固有頻率的隸屬函數得以確定。

3 葉片抗共振的模糊可靠度模型

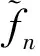
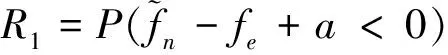
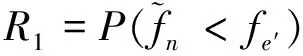
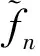
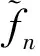
(1)

(2)

截集可靠度與所取閾值λ有關,且λ在[0,1]內可等概率隨機給出,因此可利用截集可靠度Rλ對λ的期望值作為可靠度的最終評估結果:

(3)

特別地,當固有頻率的隸屬函數在論域上恒等于1時,則任意λ所對應的截集均為整個論域,因此任意λ對應的截集可靠度均相等,與λ無關,可記為R′。由(3)式可知,此時葉片抗共振模糊可靠度R=R′。而R′為固有頻率在論域上服從概率密度gfn(fn)的常規可靠度模型,因而此時,模糊可靠度模型退化為常規可靠度模型。可見,常規可靠性模型是模糊可靠性模型的特例,是隸屬函數在論域上恒為1時的模糊模型，而模糊模型則是常規模型的補充和延伸。

4 葉片抗共振模糊可靠度模型計算

利用上述模型進行可靠性評估時,需要在截集內引入概率分布。目前常用的截集分布主要有均勻分布和線性分布[6-7]。其函數形式如下所示:

1) 均勻分布:

(4)

2) 線性分布:

(5)

4.1 模糊可靠度R的數值計算方法

利用(3)式直接計算可靠度時涉及多重積分,其解析表達式難以獲得。因此,采用數值方法計算R。由于R=Eλ[Rλ],根據數理統計理論,可用樣本均值作為期望的估計。因此在[0,1]上隨機產生一組服從均勻分布的閾值λi(i=1,2,…,Nλ),對給定的λi計算其對應的截集可靠度Rλi,則抗共振模糊可靠度R可用截集可靠度的樣本均值來近似,即:

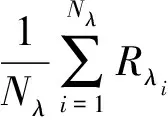
4.2 截集可靠度Rλ的計算

1) 引入均勻分布時,由(1)式和(4)式可得:

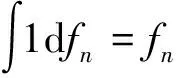
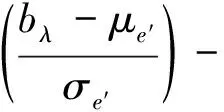
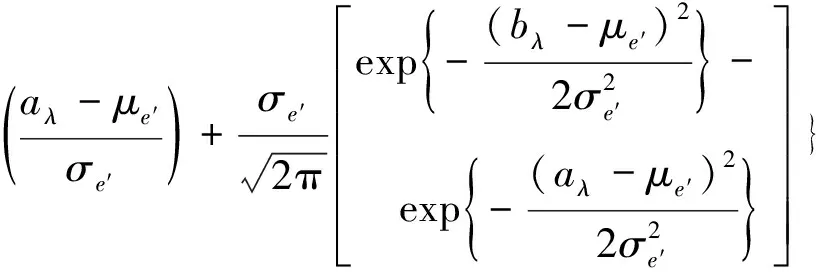
同理類似可得R2λ,進而可計算Rλ=R1λ+R2λ。

2) 引入線性分布時,由(1)式和(5)式通過推導(限于篇幅,推導過程略)可得:

同理類似可得R2λ,進而可計算Rλ=R1λ+R2λ。

5 仿真算例

5.1 確定隸屬函數的例子

由于加工、裝配精度的影響,凸肩葉片的周向接觸緊度通常落在設計值的某一公差帶內,同時又受到凸肩相對榫齒位置偏移等多種因素的干擾,偶有過緊(過松)的狀態出現。利用MATLAB軟件模擬上述過程,得到某凸肩風扇葉片模型的一組接觸緊度;根據文獻[8]接觸緊度與接觸壓力的關系式,計算出對應的凸肩接觸面壓力;再利用文獻[5]凸肩不同接觸面壓力與一彎頻率的仿真和試驗數據,擬合出凸肩接觸面壓力與一彎頻率之間函數關系,通過其計算出該葉片的一彎頻率,如表1所示。

表1 某凸肩葉片一彎頻率值

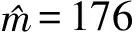
經性質檢驗發現，需對L(fn)進行非負截斷改寫。改寫后的隸屬函數如下：

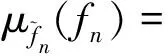
(6)

5.2 模糊方法算例

一般要求較低階振型共振裕度必須大于10%[9],因此本例中不妨取a=20。工作中當表1所示葉片受到服從隨機分布fe～N(230,10)的激振力時,使用本文模糊方法評估可得:該凸肩葉片抗一彎共振可靠度為0.989 1(均勻分布)或0.989 3(線性分布)。

圖1給出了模糊估計隨一彎頻率中值估計值的變化曲線。圖2～圖4給出了模糊估計隨各擬合參數的變化曲線。

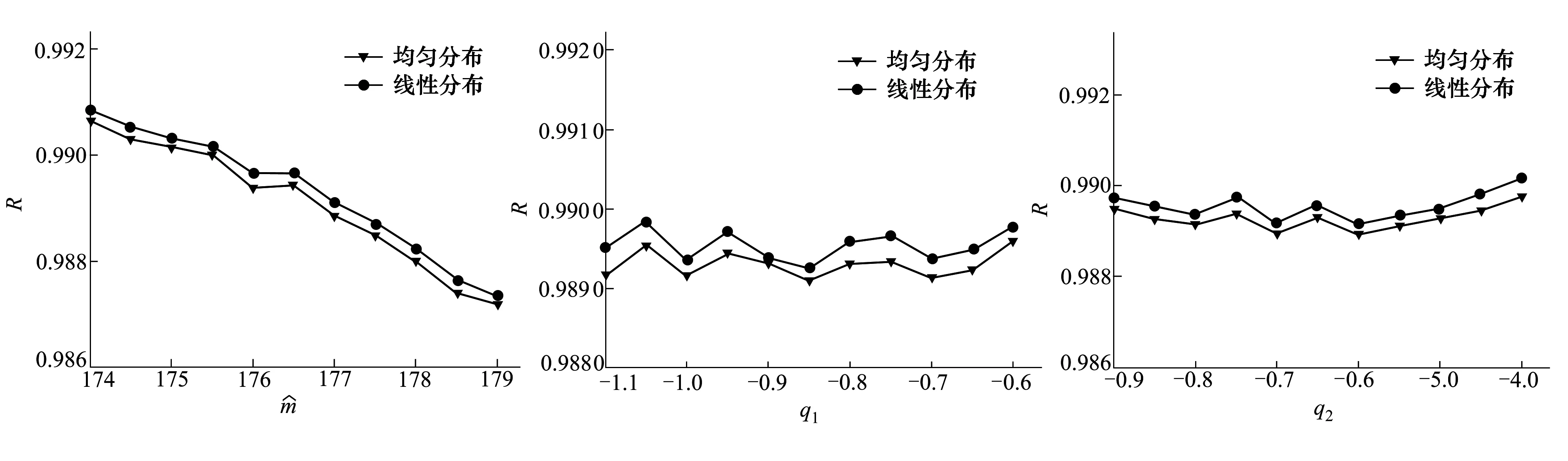
圖1 模糊估計隨的變化曲線 圖2 模糊估計隨q1的變化曲線 圖3 模糊估計隨q2的變化曲線

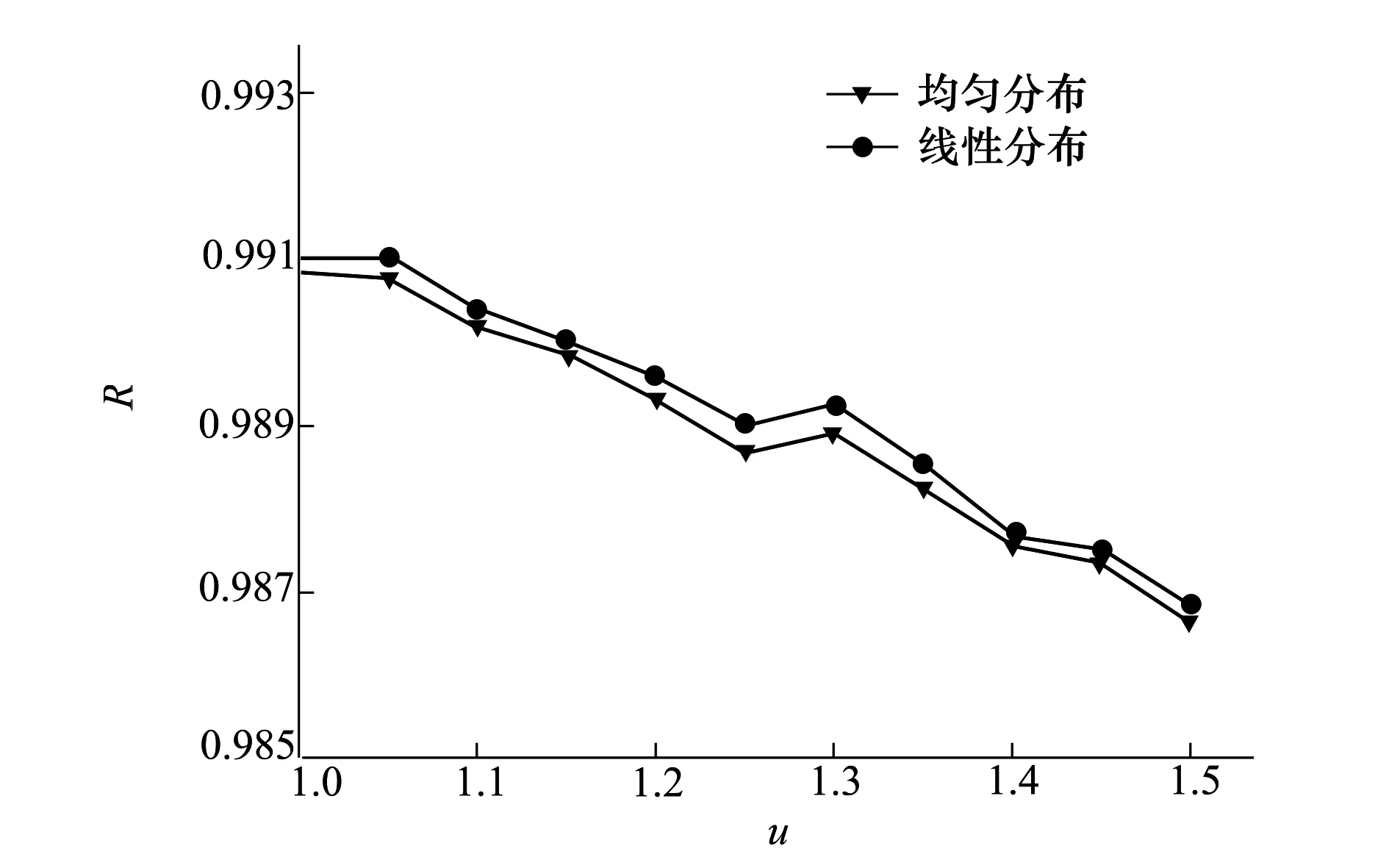
圖4 模糊估計隨擬合參數u的變化曲線

5.3 常規可靠性方法和模糊可靠性方法的比較

圖5和圖6分別給出了常規方法和模糊方法隨激振頻率均值和標準差的變化規律。由圖5可以看出,當激振頻率的均值小于130 Hz左右時,模糊方法的估計值始終小于常規方法的估計值;而當激振頻率的均值大于130 Hz左右時,無論使用何種方法,該凸肩葉片抗一彎共振可靠度均已低于97.5%,工程中還需考慮避開其他階共振,總可靠度將更低,已不滿足工程上可靠度的要求。也就是說,在工程可接受的可靠度范圍內,模糊方法估計值小于常規方法估計值。

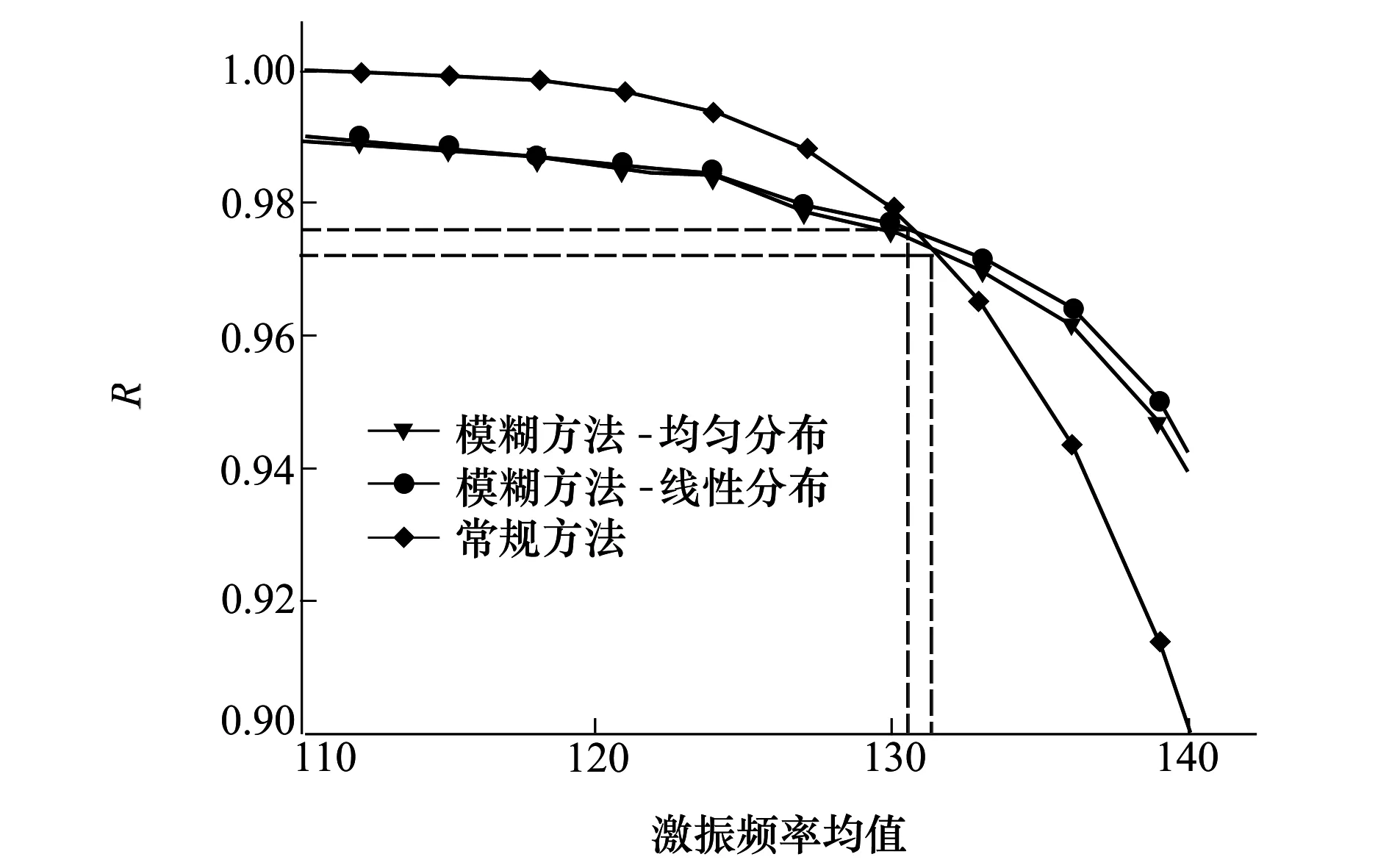
圖5 估計結果隨激振頻率均值的變化曲線

同時,圖6亦表明模糊方法的估計值小于常規方法的估計值。此外,由圖5和圖6可得:引入均勻分布時的模糊估計結果始終小于引入線性分布時的模糊估計結果。

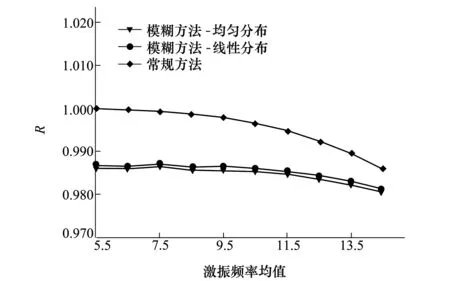
圖6 估計結果隨激振頻率標準差的變化曲線

6 結 論

本文分析了帶阻尼結構(如凸肩)葉片的固有頻率的模糊性,提出了確定固有頻率模糊隸屬函數的一種統計分析方法。同時利用截集理論建立了基于固有頻率模糊性的凸肩葉片抗共振模糊可靠度模型,并對模型進行了計算。通過分析指出常規模型是模糊模型的特例,模糊方法是當系統具有模糊性時,對常規方法的補充,為處理模糊現象提供了一種途徑。最后通過算例表明:本文所提模糊方法對葉片固有頻率中值估計值及隸屬函數擬合參數具有較好的穩定性,其估計結果略小于常規方法估計結果。

參考文獻：

[1] Zio E. Reliability Engineering: Old Problems and New Challenges [J]. Reliability Engineering and System Safety, 2009, 94(2): 125-141

[2] 皮福德. 結構振動模糊可靠性分析方法及應用研究[D]. 西安: 西北工業大學, 2006

Pi Fude. Study on the Structural Vibration Fuzzy Reliability Analysis Method and Its Application [D]. Xi′an: Northwestern Polytechnical University, 2006 (in Chinese)

[3] 徐可君,江龍平,隋育松. 應用模糊方法計算構件振動可靠性[J]. 機械強度,2003, 25(5): 523-526

Xu Kejun, Jiang Longping, Sui Yusong. Applying Fuzzy Method to Assessment Vibration Reliability of Structural Components [J]. Journal of Mechanical Strength, 2003, 25(5): 523-526 (in Chinese)

[4] 馬利,張恒喜,續斌,等. 航空發動機重要構件使用振動可靠性模糊評估[J]. 機械科學與技術, 2006, 11(25): 1365-1368

Ma Li, Zhang Hengxi, Xu Bin, et al. Fuzzy Estimation of Aeroengine Blades Operational Vibration Reliability[J]. Mechanical Science and Technology, 2006, 11(25): 1365-1368 (in Chinese)

[5] 張海洋. 風扇葉片凸肩減振效果研究[D]. 北京：中國航空研究院, 2011

Zhang Haiyang. The Shroud Fan Blade Design for Reducing the Vibration [D]. Beijing: Chinese Aeronautical Establishment, 2011 (in Chinese)

[6] 董玉革,朱文予,陳心昭. 機械模糊可靠性計算方法的研究[J]. 系統工程學報, 2000, 15(1):7-12

Dong Yuge, Zhu Wenyu, Chen Xinzhao. Study on a Calculating Method of Machine Fuzzy Reliability [J]. Journal of Systems Engineering, 2000, 15(1): 7-12 (in Chinese)

[7] Jiang Q M, Chen C H. A Numerical Algorithm of Fuzzy Reliability [J]. Reliability Engineering and System Safety, 2003, 80: 299-307

[8] 李文明. 鋸齒冠的結構特性與設計[J]. 航空發動機, 2009,35(1):17-21

Li Wenming. Structural Characteristics and Design of Serrated Shroud [J]. Aeroengine, 2009, 35(1): 17-21 (in Chinese)

[9] 李宏新,張連祥,王延榮,等. 風扇工作葉片振動可靠性評估[J]. 航空發動機,2003, 29(1): 17-19

Li Hongxin, Zhang Lianxiang, Wang Yanrong, et al. Estimation of Fan Blade Vibration Reliability for a Turbofan Engine [J]. Aeroengine, 2003, 29(1): 17-19 (in Chinese)