載荷AUV進水過程分析及分離運動仿真

潘光, 魏靜, 陳誠

(1.西北工業大學 航海學院, 陜西 西安 710072; 2.解放軍第94857部隊, 安徽 蕪湖 241007)

近些年來，隨著AUV相關技術的日趨成熟，其已經逐漸稱為各種背景下的海洋水下任務中的首選工具。載荷分離AUV隨著AUV相關技術的發展以及商業和科研等多方面需求而出現的新型AUV。與現有的其他類AUV相比，多載荷AUV可以同時攜帶多個不同的工作載荷，從而大大提高了AUV的利用率以及經濟性。多載荷AUV攜帶的是多個不同的獨立載荷，每個載荷都是一個自封閉的子系統，不同載荷之間僅通過分離機構等連接裝置相串接，當不發生分離時，其與多模塊AUV并無區別，而通過分離，多載荷AUV可以實現不同載荷之間的完全獨立工作，即不同任務、不同地點，這正是現有的其他各類AUV所缺乏的。

但是，當AUV施放載荷時，稍有不慎就有分離后的載荷和運載體發生撞擊而導致分離失敗的可能，所以，對AUV分離運動過程及分離安全性進行研究具有極高的實用價值。基于以上背景本文對載荷AUV分離進水過程，分離及過程分離后載荷的彈道進行了研究。

1 載荷AUV分離進水過程分析

本文建立的載荷AUV模型是無推力推動的，且具有前后2個平衡艙段和中間的1級載荷段3個部分，其中前平衡艙在航行初期通過進水來增加載荷AUV的重力，隨著重心的變化使其在航行中逐步旋轉下潛至分離方位，同時后平衡艙開始進水，隨著重力的增加和重心的偏移，后平衡艙依靠重力分離，載荷脫離開始自由航行到達預定位置，完成既定任務。由此可見載荷AUV在分離運動時，通過進水以增加其負浮力，從而實現分離要求，故進水過程的研究與分析具有極高的實用價值。

前、后平衡艙空腔的進水過程屬于涉及空氣、海水的氣液兩相流問題，過程較為復雜。本文運用基于計算流體力學的VOF多相流技術[1]，針對前、后平衡艙空腔在靜止情況下進水過程進行數值模擬，以得到進水體積及質量隨時間的變化過程，避免加工模型水池實驗所帶來的周期長、費用高等問題。

為了簡化考慮，也將前、后平衡艙的密封空氣當作不可壓縮流體處理，本文中的進水過程即屬于互不摻混的不可壓縮氣/液兩相流問題的范疇[1-2]。則對于整個計算域而言，控制方程[1-2]可表示為：

液相：

(1)

氣相:

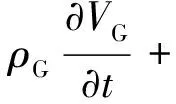
(2μGDG)+ρGf·VG=0

(2)

式中：下標L和G分別表示液體和氣體。對于體積力,僅考慮重力的作用,則f即為重力加速度向量。

為精確模擬進水過程,計算域全部采用結構化多塊網格劃分的思路,最終生成了高質量的內外流場網格,計算生成了一系列前后平衡倉進水過程的進水云圖,通過計算模擬的方式的展示了前后平衡倉進水全過程,以進水后期的前后平衡艙的進水云圖為例,從圖1、圖2可以看出,進水效率較高,最終的進水體積前平衡倉可以達到92%,后平衡倉可以達到95%,滿足無推沖作用下的載荷分離條件。

圖1 前平衡艙進水云圖

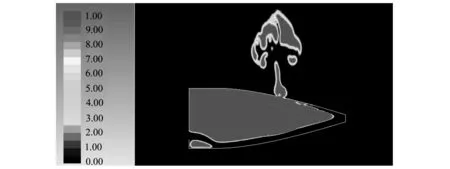
圖2 后平衡艙進水云圖

2 載荷AUV分離彈道仿真

當載荷AUV在前平衡艙進水的過程中運行到某一預定分離點后,在航行過程中后平衡艙開始進水,到達分離點實現與搭載單元分離,分離后載荷繼續自由航行,最終降落到某一位置。載荷在分離后的航行中,有可能發生觸底、和搭載單元尾部碰撞等現象。彈道仿真的目的就是通過分離姿態及運行軌跡等的仿真,得到載荷是否安全分離,是否降落到預定的位置的結果。

2.1 空間運動動力學模型

推導載荷AUV的動力學方程之前,首先假設:

① 載荷AUV單元為剛體;

② 載荷AUV完全浸沒在流體介質中,并處于全黏濕狀態。

載荷AUV的位置在地面坐標系中表示為r=[x0,y0,z0]T,在體坐標系中載荷AUV速度描述為v=[vx,vy,vz]T,在地面坐標系中描述其姿態為Θ=[θ,ψ,φ]T,角速度描述為ω=[ωx,ωy,ωz]T[6],載荷AUV在航行過程中具有進水過程,因此在航行過程中其質量隨時間是不斷變化的,因此必須考慮變質量的問題。相關的參數有:質量、重力、重心位置、轉動慣量及慣性積。由于本文研究的是縱向運動則載荷AUV的運動學方程組[5-6]為:

(3)

(4)

式中：Amλ為慣性矩陣,Avω為速度矩陣,AFM為力矩陣,且

式中：

在此需要特別注意的是雖然分離前AUV整體及分離后載體段與載荷段的運動都是建立在以其各自浮心為原點的體坐標系中的,但是由于分離運動造成坐標原點的改變使得開始分離后載體段和載荷段的初始條件變得較為復雜。由于分離之后新的坐標原點和舊的坐標原點不重合,故不能把AUV分離前一時刻的運動參數作為分離后載荷段和載體段的初始條件,因此將舊體坐標系(AUV浮心為原點的體坐標系)中的載體段和載荷段的坐標投影到地面坐標系中得到載體段和載荷段的初始坐標,再通過坐標轉換得到載體段和載荷段最終的運動初始條件進行下一步的計算。

2.2 典型工況下的彈道仿真結果

以載荷段用于布雷為例(即分離后載荷段具有錨雷的特性),本文研究了不同進水時間及不同初始速度條件下載荷AUV彈道曲線及分離后載荷的彈道曲線,具體如下:

1) 前平衡艙不同進水時間的載荷AUV分離彈道仿真結果

設定彈道傾角為-60°時到達載荷分離時刻,假設初始深度為-10 m,海底深度為-150 m,載荷AUV初始速度vx為2.57 m/s,vy為0,vz為0,俯仰角θ為0,前平衡艙進滿水的時間不同對載荷段和后平衡艙段分離及其分離后的航行具有很大的影響,因此本文對前平衡艙進水時間為3 s、5 s的工況做了彈道仿真,結果如下:

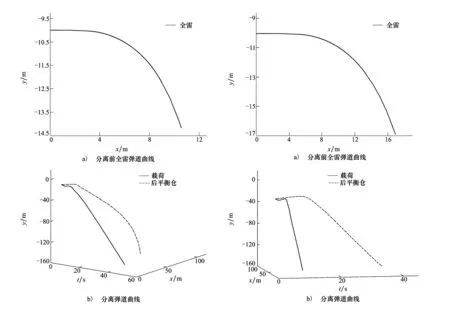
圖3 前平衡倉進水3 s時彈道仿真結果示意圖 圖4 前平衡倉進水5 s時彈道仿真結果示意圖

通過仿真得到的彈道曲線(見圖3和圖4)可以看出,前平衡艙進滿水的時間越短,雷體到達分離狀態的時間越短,航行損耗越小,而且分離后水雷的彈道軌跡與后平衡艙的彈道軌跡沒有相交的部分,證明分離后的動作過程中水雷不會與后平衡艙相碰,具有可靠的安全性。

2) 不同航行速度的載荷AUV分離彈道仿真結果

設定彈道傾角為-90°時到達載荷分離時刻,按照水池實驗模型條件,假設初始深度為-0.5 m,海底深度為-150 m,載荷AUV初始速度vx不定,vy為0,vz為0,俯仰角θ為0,平衡艙進水速度不變的情況下,由于載荷AUV初始速度vx不同對載荷段和后平衡艙段分離及其分離后的航行具有很大的影響,因此本文對初始速度vx為0 kn,2 kn的工況做了彈道仿真,結果如下:

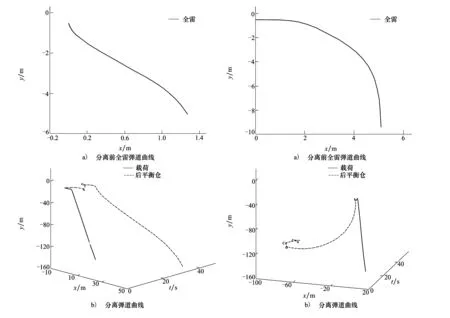
圖5 初始速度為0 kn時彈道仿真結果示意圖 圖6 初始速度為2 kn時彈仿真結果示意圖

按照水池實驗模型條件，利用所建立的數學模型對其分離彈道進行仿真，仿真結果(見圖5、圖6)與實驗結果吻合較好，同時也證明了在不大于2 kn速度航行分離后載荷的彈道軌跡與后平衡艙的彈道軌跡沒有相交的部分，證明了彈道仿真結果的可靠性。

3 結 論

本文運用基于計算流體力學的VOF多相流技術，針對載荷AUV前、后平衡艙空腔在靜止情況下的進水過程進行了數值模擬，以得到進水體積及質量隨時間的變化過程，并對前平衡艙不同進水速度及不同初始速度作用下載荷AUV的彈道及分離后載荷的彈道進行了仿真，并與水池實驗結果進行比對分析，證明了彈道仿真結果的可靠性。研究結果具有一定的工程應用價值，對多載荷AUV水下分離運動進一步的研究具有指導意義。

參考文獻：

[1] 劉儒勛, 舒其望. 計算流體力學的若干新方法[M]. 北京: 科學出版社,2003

Liu Ruxun, Shu Qiwang. Several New Methods of Calculate Fluid Dynamics[M]. Beijing: Science Press,2003 (in Chinese)

[2] Kalland K M. A Navier-Stokes Solver for Single-And Two-Phase Flow[D]. University of Oslo, 2008

[3] Sussman M, Smith K M, Hussaini M Y, et al. A Sharp Interface Method for Incompressible Two-Phase Flows[J]. Journal of Computational Physics, 2007, 221(2): 469-505

[4] 黃景泉, 張宇文. 魚雷流體力學[M]. 西安：西北工業大學出版社, 1989

Huang Jingquan, Zhang Yuwen. Torpedo Hydromechanics[M]. Xi′an: Northwestern Polytechnical University Press, 1989 (in Chinese)

[5] 張宇文. 魚雷彈道與彈道設計[M]. 西安：西北工業大學出版社, 1999

Zhang Yuwen. Torpedo Trajectory and Trajectory Design[M]. Xi′an: Northwestern Polytechnical University Press, 1999 (in Chinese)

[6] 潘光，杜曉旭，宋保維，等. 魚雷力學[M]. 西安：陜西師范大學出版社,2013

Pan Guang, Du Xiaoxu, Song Baowei, et al. Torpedo Mechanics[M]. Xi′an: Shaanxi Normal University Press, 2013 (in Chinese)

[7] 宋保維，趙娥，邵成，等. AUV重力加小推沖載荷分離方法[J]. 魚雷技術,2008, 16(1):7-10

Song Baowei, Zhao E, Shao Cheng, et al. A Method for Load Separation from Head of Autonomous Underwater Vehicle Using Load Gravity and Suitable Thrust[J]. Torpedo Technology, 2008, 16(1):7-10 (in Chinese)

[8] 潘瑛, 徐德民. AUV水下分離運動及分離方式研究[J]. 西北工業大學學報, 2004, 22(4): 505-509

Pan Ying, Xu Demin. On the Kinematics and Mode Selection for Separation Motion of AUV[J]. Journal of Northwestern Polytechnical University, 2004, 22(4): 505-509 (in Chinese)

[9] 邵成, 宋保維. 攜帶正浮力載荷AUV的載荷分離運動仿真研究[J]. 系統仿真學報,2008,20(9):2454-2457

Shao Cheng, Song Baowei. Simulation of AUV Load Separation Motion with Positive Buoyancy Force Load[J]. Journal of System Simulation. 2008, 20(9): 2454-2457 (in Chinese)