基于流固耦合方法的大展弦比機(jī)翼非線性顫振特性分析

馬艷峰, 賀爾銘, 曾憲昂, 李俊杰, 唐長(zhǎng)紅

(1.西北工業(yè)大學(xué) 航空學(xué)院, 陜西 西安 710072; 2.中航工業(yè)第一飛機(jī)設(shè)計(jì)研究院, 陜西 西安 710089)

大型運(yùn)輸機(jī)、高空長(zhǎng)航時(shí)無(wú)人機(jī)都具有展弦比大、柔性大、變形大等特點(diǎn)，飛機(jī)在飛行載荷作用下會(huì)產(chǎn)生彎曲和扭轉(zhuǎn)變形，一方面結(jié)構(gòu)平衡狀態(tài)相對(duì)于未變形結(jié)構(gòu)有一定差異，結(jié)構(gòu)存在預(yù)應(yīng)力，各振型和頻率也有差別；另一方面，變形前后氣動(dòng)面的差異也會(huì)導(dǎo)致非定常氣動(dòng)力的不同。這兩方面綜合將使機(jī)翼的顫振特性發(fā)生變化[1]。

隨著數(shù)學(xué)計(jì)算工具的進(jìn)步和對(duì)復(fù)雜系統(tǒng)非線性空氣動(dòng)力學(xué)認(rèn)識(shí)的加深，飛行器顫振問(wèn)題得到了更深入研究。在20世紀(jì)90年代早期, Van Schoor等[2]基于完全線性理論對(duì)一個(gè)大柔性飛機(jī)進(jìn)行了氣動(dòng)彈性分析, 討論了結(jié)構(gòu)彈性對(duì)氣動(dòng)彈性和飛行動(dòng)力學(xué)穩(wěn)定性的影響。Patil等[3]研究了高空長(zhǎng)航時(shí)飛行器的氣動(dòng)穩(wěn)定性和飛行力學(xué)特性, 并在考慮幾何非線性的基礎(chǔ)上, 分析了大展弦比機(jī)翼的顫振特性。Mayuresh和Dowell[4]結(jié)合理論和實(shí)驗(yàn)方法研究了大展弦比機(jī)翼的氣動(dòng)彈性相應(yīng)問(wèn)題, 并由此掀起了大展弦比機(jī)翼非線性氣動(dòng)彈性研究的熱潮[5-6]。國(guó)內(nèi)方面，楊智春等[7]研究了非線性大展弦比柔性機(jī)冀模型的靜氣動(dòng)彈性特性, 并通過(guò)提取靜平衡位置的剩余剛度, 計(jì)算了顫振特性。謝長(zhǎng)川、楊超[8]基于動(dòng)力學(xué)小擾動(dòng)假設(shè)，建立了具有大展弦比機(jī)翼柔性飛機(jī)的全機(jī)幾何非線性氣動(dòng)彈性穩(wěn)定性分析的線性化方法和工程求解流程。崔鵬、韓景龍[9]考慮了幾何非線性，進(jìn)行了切尖三角翼的非線性顫振和極限環(huán)振蕩的研究。

本文綜合考慮機(jī)翼結(jié)構(gòu)的幾何非線性和氣動(dòng)力非線性，詳細(xì)地分析了大展弦比機(jī)翼的非線性顫振特性。以平板機(jī)翼為例，計(jì)算了機(jī)翼在不同攻角下的靜彈性變形、模態(tài)特性以及顫振特性。通過(guò)比較顫振計(jì)算線性解與非線性解的差別，說(shuō)明對(duì)大展弦比機(jī)翼進(jìn)行顫振分析時(shí)，必須同時(shí)考慮結(jié)構(gòu)幾何非線性和氣動(dòng)力非線性。

1 計(jì)算方法

常規(guī)顫振計(jì)算采用偶極子網(wǎng)格法計(jì)算非定常氣動(dòng)力，當(dāng)結(jié)構(gòu)發(fā)生變形，偶極子網(wǎng)格無(wú)法跟隨結(jié)構(gòu)運(yùn)動(dòng)形成曲面，因此它不適用于大變形的非線性顫振分析。針對(duì)大變形計(jì)算氣動(dòng)網(wǎng)格要跟隨結(jié)構(gòu)形成曲面的特點(diǎn)[10]，本文選用非定常渦格法來(lái)求解非定常氣動(dòng)力，渦格的形狀較為靈活，沿展向2條端線也無(wú)須滿足平行于來(lái)流的限制，可形成任意曲面形狀[10-11]，另外一個(gè)主要差別是用渦格法計(jì)算非定常流動(dòng)時(shí)采用時(shí)域法，比偶極子網(wǎng)格多出了從后緣到遠(yuǎn)場(chǎng)的尾渦網(wǎng)格。

1.1 渦格模型

渦格模型示意圖如圖1所示[12]。將拓展到遠(yuǎn)場(chǎng)的馬蹄渦拆分成若干個(gè)獨(dú)立渦格，而這些渦格一部分附著于物面上，一部分則形成尾渦，將尾渦網(wǎng)格布置到距翼面后緣30倍弦長(zhǎng)為止。

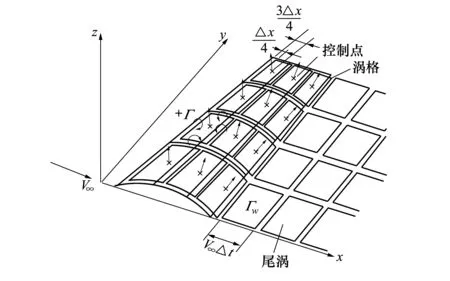
圖1 渦格模型示意圖

設(shè)物面上的渦格共有N=Nc·Ns個(gè)(Nc為物面沿弦向的網(wǎng)格數(shù),Ns為沿展向的網(wǎng)格數(shù)),尾渦格共M=Nw·Ns個(gè)(Nw為尾渦沿弦向的網(wǎng)格數(shù)),則法向洗流速度和渦強(qiáng)度的關(guān)系可寫成如下的矩陣形式[11]:

(1)

式中：上標(biāo)‘～’表示尾渦。

對(duì)于定常問(wèn)題:

vn=-V∞·n

(2)

對(duì)于非定常問(wèn)題:

vn=(Vs-V∞)·n

(3)

式中：Vs為物體在該控制點(diǎn)處的運(yùn)動(dòng)速度,對(duì)于非定常問(wèn)題,單元法向矢量n隨物體的運(yùn)動(dòng)而不斷變化。

1.2 載荷計(jì)算

渦格上作用的空氣動(dòng)力與渦強(qiáng)度有關(guān),它由兩部分組成,一部分是與渦強(qiáng)度時(shí)間導(dǎo)數(shù)相關(guān)的Ft,另一部分是與渦強(qiáng)度空間導(dǎo)數(shù)相關(guān)的Fs。

(4)

式中：ρ∞為來(lái)流密度,S為渦格面積。Ft作用于渦格的中心,方向沿單元的法向。

當(dāng)渦格位于機(jī)翼前緣時(shí):

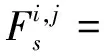
i=(m-1)·Nc+1,m=1,2,…,Ns

(5)

當(dāng)渦格不位于機(jī)翼前緣時(shí):

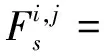
i≠(m-1)·Nc+1,m=1,2,…,Ns

(6)

式中:b為渦格沿展向的跨度,FS作用于渦格前端渦線的中點(diǎn),方向沿單元的法向,通過(guò)杠桿原理將Ft和Fs分配到角點(diǎn)上[11]。

1.3 增量法求結(jié)構(gòu)靜變形

本文只考慮翼面大變形產(chǎn)生的幾何非線性影響,不考慮材料非線性等因素,采用增量法計(jì)算,結(jié)構(gòu)的增量平衡方程如下:

KTΔq=ΔP-ΔR

(7)

式中：ΔP為載荷增量,ΔR為內(nèi)力增量,Δq為增量位移,KT為切線剛度矩陣:

KT=K0+Kσ

(8)

式中：K0為線彈性剛度矩陣,Kσ為幾何剛度矩陣(初應(yīng)力陣)。

1.4 模態(tài)分析

在變形后的平衡位置求結(jié)構(gòu)響應(yīng)還需求解結(jié)構(gòu)在該位置的動(dòng)態(tài)特性,在平衡位置的結(jié)構(gòu)動(dòng)力方程為:

(9)

通過(guò)模態(tài)法求解該方程,將(9)式表示為模態(tài)坐標(biāo)下的減縮形式如下:

(10)

1.5 分析流程圖

本文使用改進(jìn)的“松耦合”方式來(lái)聯(lián)合推進(jìn)結(jié)構(gòu)和氣動(dòng)方程。分析時(shí)尋求二者之間的匹配關(guān)系,顫振速壓即為產(chǎn)生靜彈變形的速壓,靜彈變形則為顫振分析的平衡狀態(tài)。反復(fù)進(jìn)行靜彈和顫振計(jì)算,不斷迭代使二者關(guān)系達(dá)成一致,圖2給出了分析流程圖。

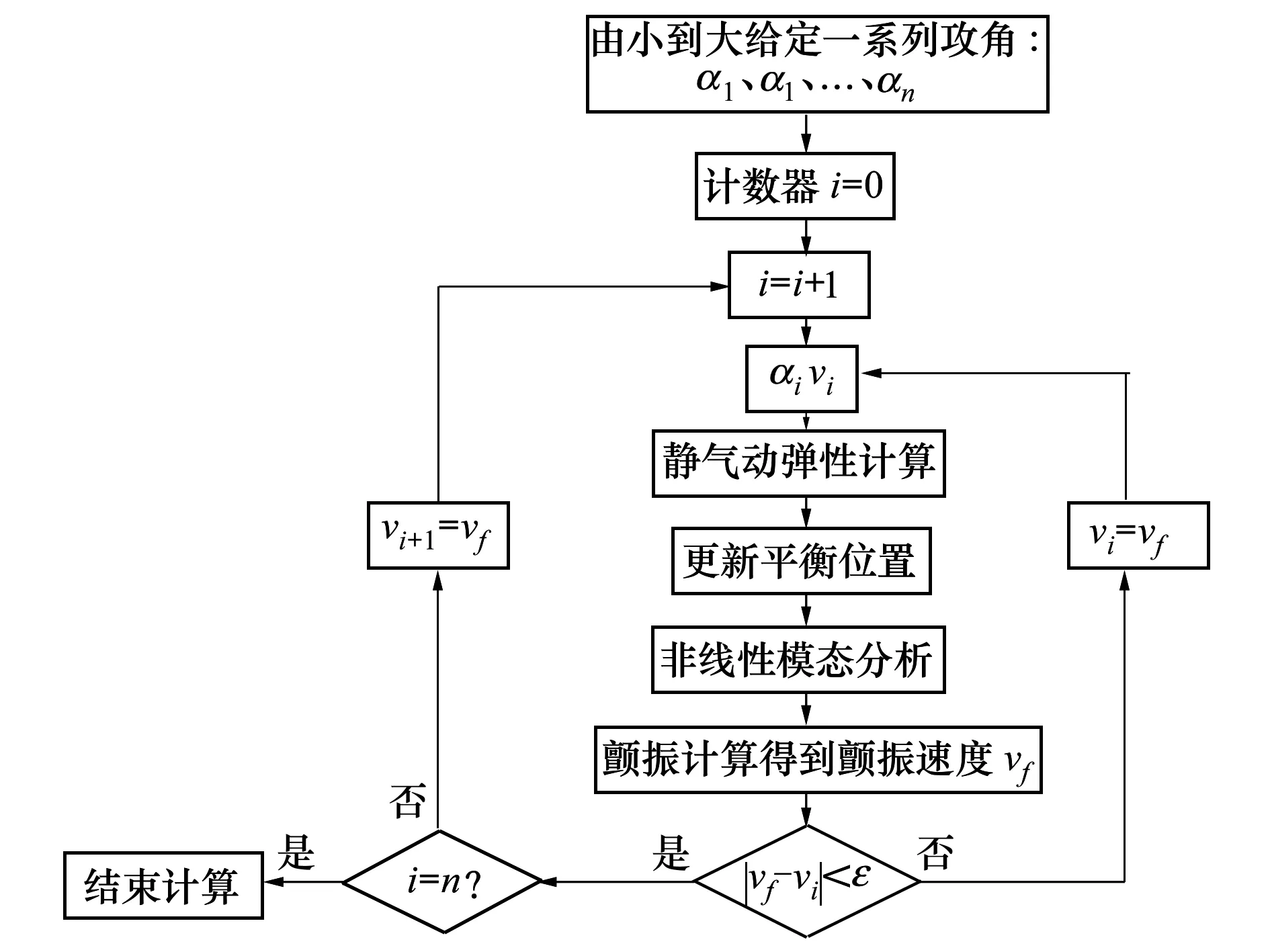
圖2 非線性顫振分析流程圖

2 非定常氣動(dòng)力驗(yàn)證

建立一個(gè)展弦比為24的長(zhǎng)直機(jī)翼,網(wǎng)格數(shù)為20×40,給它施加一個(gè)強(qiáng)迫俯仰運(yùn)動(dòng):

?=?msin(kt)

(11)

式中:?m為俯仰角的振幅,k為減縮頻率,t為無(wú)量綱時(shí)間,轉(zhuǎn)動(dòng)的軸線為機(jī)翼沿展向的中心線,減縮頻率k=0.2時(shí),升力和俯仰力矩響應(yīng)歷程與經(jīng)典theodorson理論計(jì)算結(jié)果比較如圖3所示。二者的響應(yīng)曲線吻合好,驗(yàn)證了渦格法計(jì)算的正確性。

圖3 渦格法與theodorson氣動(dòng)力的比較(k=0.2)

3 算例及結(jié)果分析

3.1 計(jì)算模型

計(jì)算選用的平板機(jī)翼根弦長(zhǎng)為1 m,根梢比為1,展長(zhǎng)為4 m,展弦比為4,前緣后掠角為8°。結(jié)構(gòu)模型如圖4所示,平板的厚度為0.03 mm,材料彈性模量E=71 GPa,密度為2 700 kg/m3,泊松比為0.33。主要前5階振動(dòng)頻率見表1。

圖4 結(jié)構(gòu)有限元模型

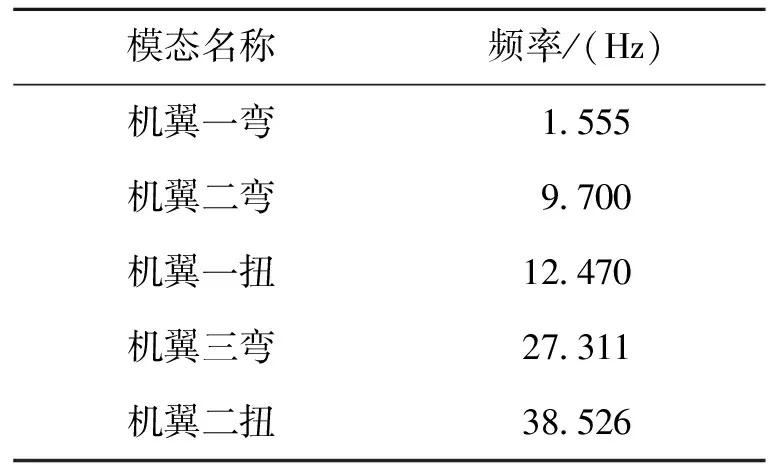
表1 主要振型及頻率

氣動(dòng)網(wǎng)格分為物面網(wǎng)格和尾渦網(wǎng)格兩部分,物面網(wǎng)格數(shù)量為20×30,與結(jié)構(gòu)網(wǎng)格數(shù)一致,為了便于數(shù)據(jù)交換,尾渦網(wǎng)格一致延伸到距后緣30倍弦長(zhǎng)。

3.2 線性顫振分析

來(lái)流密度ρ∞=2 kg/m3,通過(guò)調(diào)整來(lái)流速度,判斷結(jié)構(gòu)響應(yīng)是否等幅震蕩來(lái)判斷是否發(fā)生臨界顫振,得到Vf=171.47 m/s,ωf=6.115 Hz。在顫振速度下的廣義位移響應(yīng)如圖5所示。由圖可見,顫振形態(tài)是典型的彎扭耦合型顫振,參與顫振的模態(tài)主要是機(jī)翼一彎、二彎和一扭。

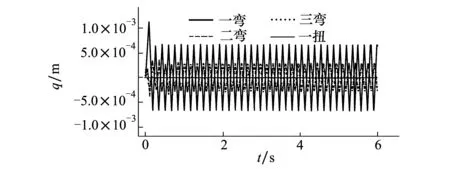
圖5 廣義位移響應(yīng)

3.3 非線性顫振分析

計(jì)算攻角取α=0°～10°,攻角增量的間隔取Δα=1°。當(dāng)α1=0°時(shí),取v1=171.47 m/s。按圖2所示的流程圖進(jìn)行靜彈和顫振的匹配計(jì)算。顫振速度和頻率隨攻角的變化如圖6、圖7和表2所示。

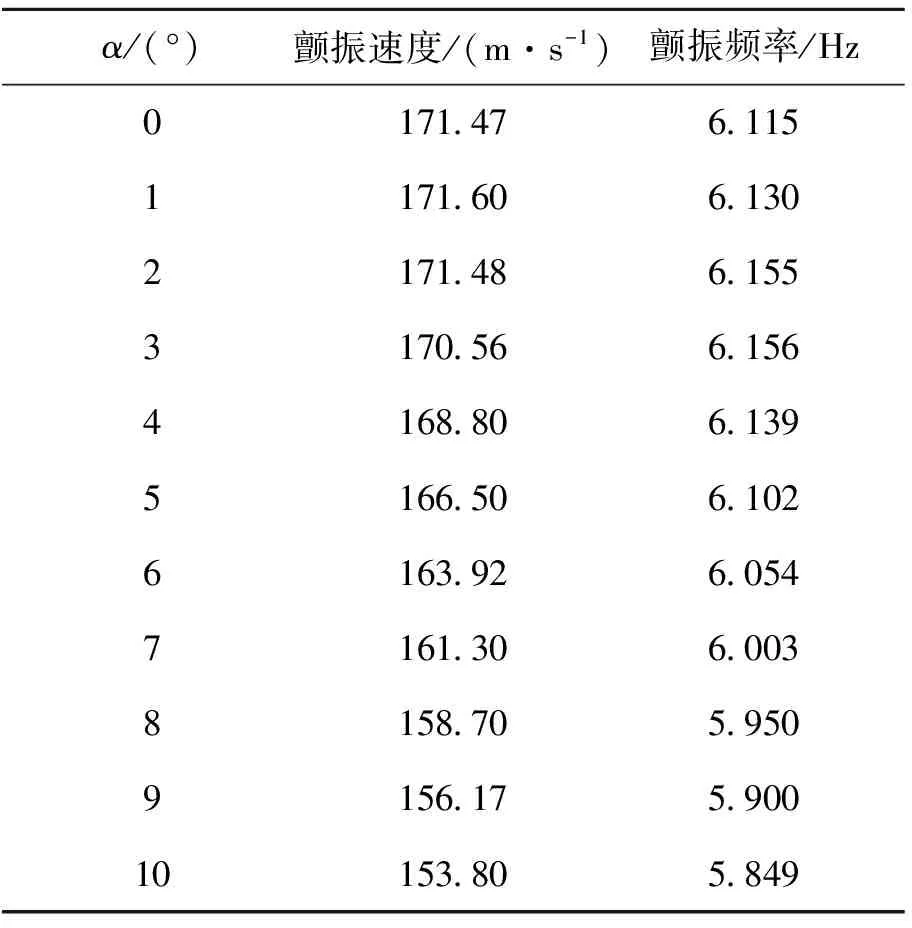
表2 顫振速度和頻率隨攻角的變化

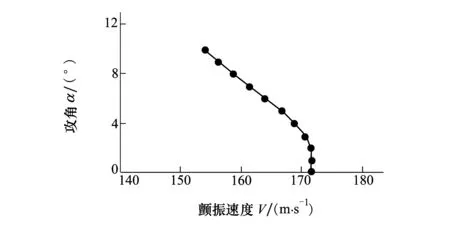
圖6 顫振速度隨攻角的變化

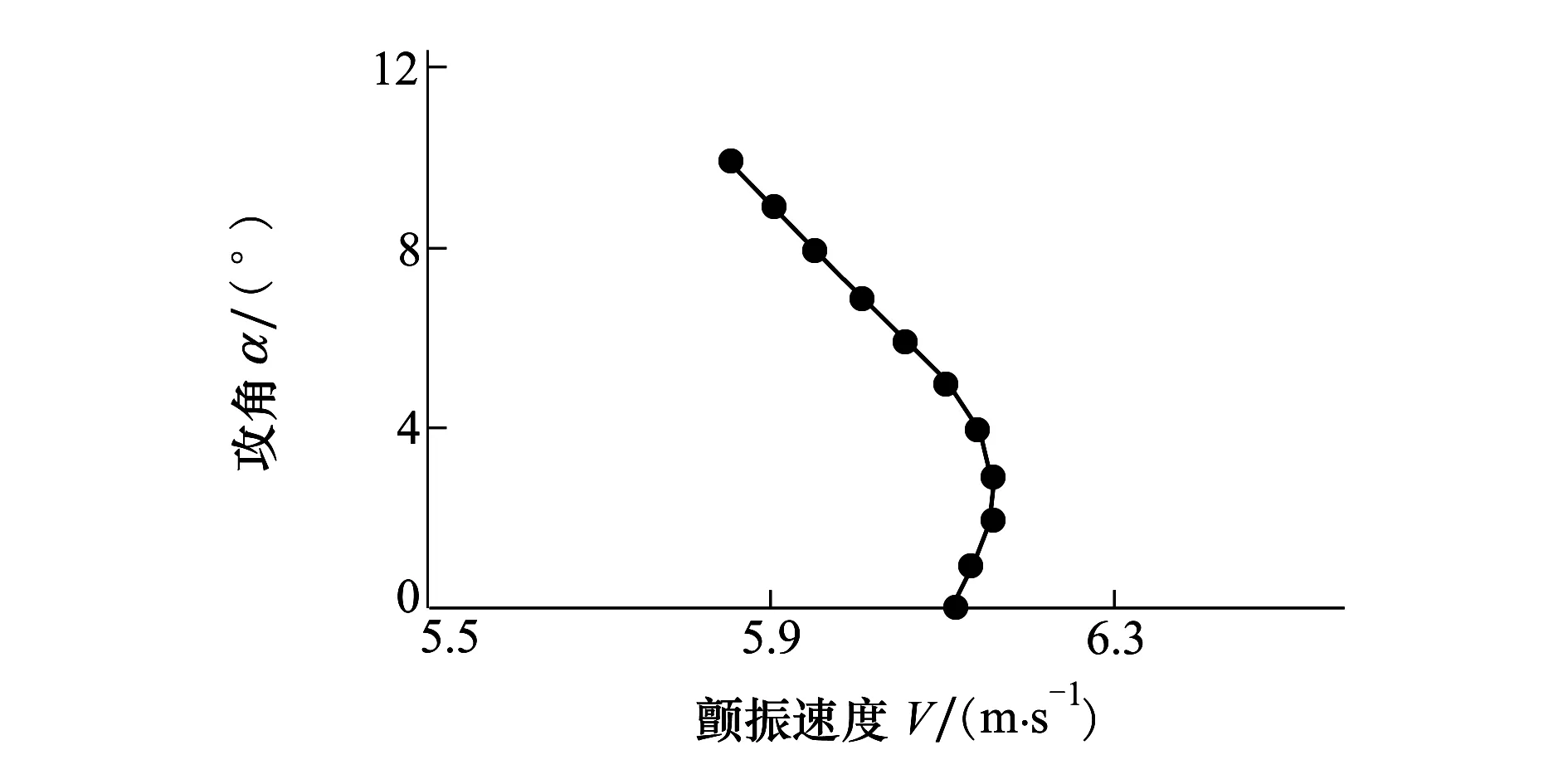
圖7 顫振頻率隨攻角的變化

圖8 不同攻角,顫振速壓下,機(jī)翼前緣的靜變形

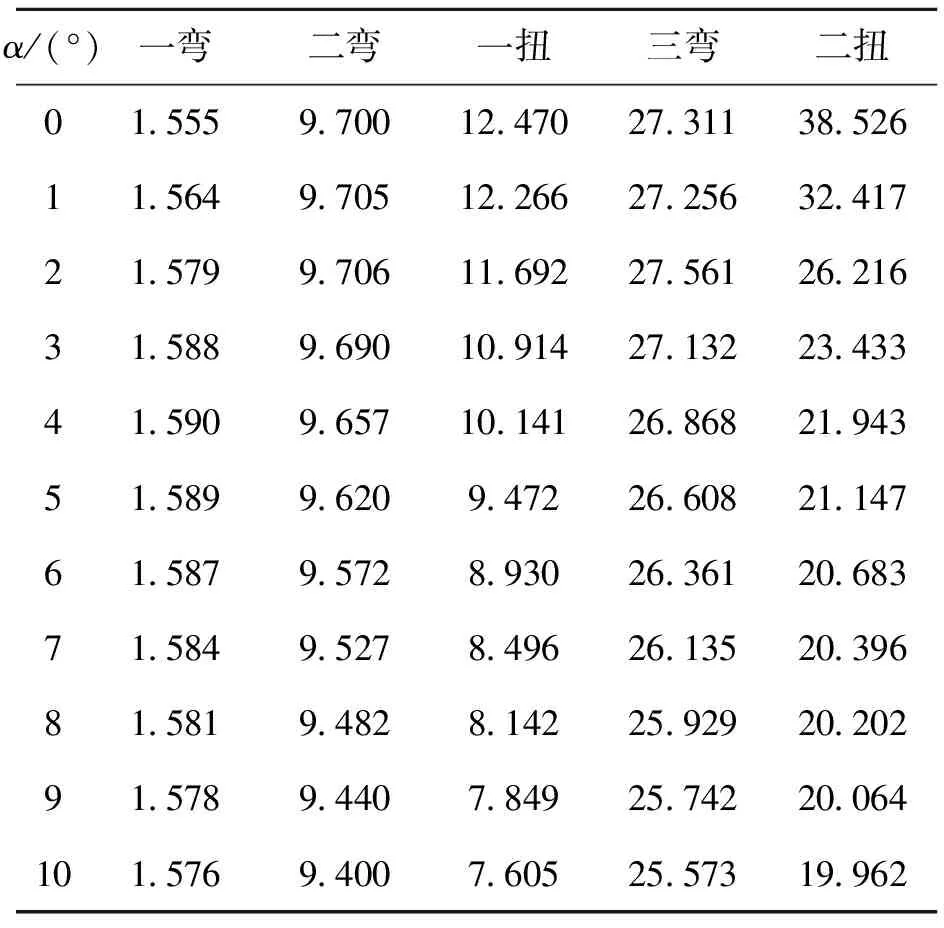
表3 不同攻角下機(jī)翼平衡位置的模態(tài)頻率

如圖6可見,顫振速度呈現(xiàn)出隨攻角先略微增大,后逐漸減小的過(guò)程(拐點(diǎn)在α≈2°),說(shuō)明結(jié)構(gòu)非線性將給顫振帶來(lái)不利影響。圖8給出了機(jī)翼前緣線隨攻角的變化,由于結(jié)構(gòu)非線性的影響,隨著攻角的增大,每1°攻角產(chǎn)生的位移增量逐漸減小。表3給出了振動(dòng)模態(tài)的頻率隨攻角的變化,隨著攻角的增大,機(jī)翼彎曲頻率變化幅度不大,相比之下扭轉(zhuǎn)頻率減小的幅度很大,10°攻角時(shí)機(jī)翼一扭頻率只有0°攻角時(shí)機(jī)翼一扭頻率的61%,這也正是顫振速度隨攻角減小的主要原因。

3.4 結(jié)果比較

以下討論不考慮非線性或是部分考慮非線性對(duì)計(jì)算結(jié)果的影響。對(duì)以下3種情況的計(jì)算結(jié)果進(jìn)行比較:

a) 結(jié)構(gòu)非線性+氣動(dòng)力非線性;

b) 結(jié)構(gòu)非線性+氣動(dòng)力線性;

c) 結(jié)構(gòu)線性+氣動(dòng)力線性

結(jié)果如圖9所示。可見,當(dāng)只考慮結(jié)構(gòu)非線性變形,氣動(dòng)網(wǎng)格不隨平衡位置變化時(shí),計(jì)算出來(lái)的顫振速度變化趨勢(shì)與考慮氣動(dòng)網(wǎng)格變化的結(jié)果趨勢(shì)完全相反,原因解釋如下:

圖9 考慮非線性對(duì)計(jì)算結(jié)果的影響

如圖10所示,非線性模態(tài)振型基本垂直于變形后的網(wǎng)格,若氣動(dòng)網(wǎng)格隨結(jié)構(gòu)變化,則(2)式中vn=

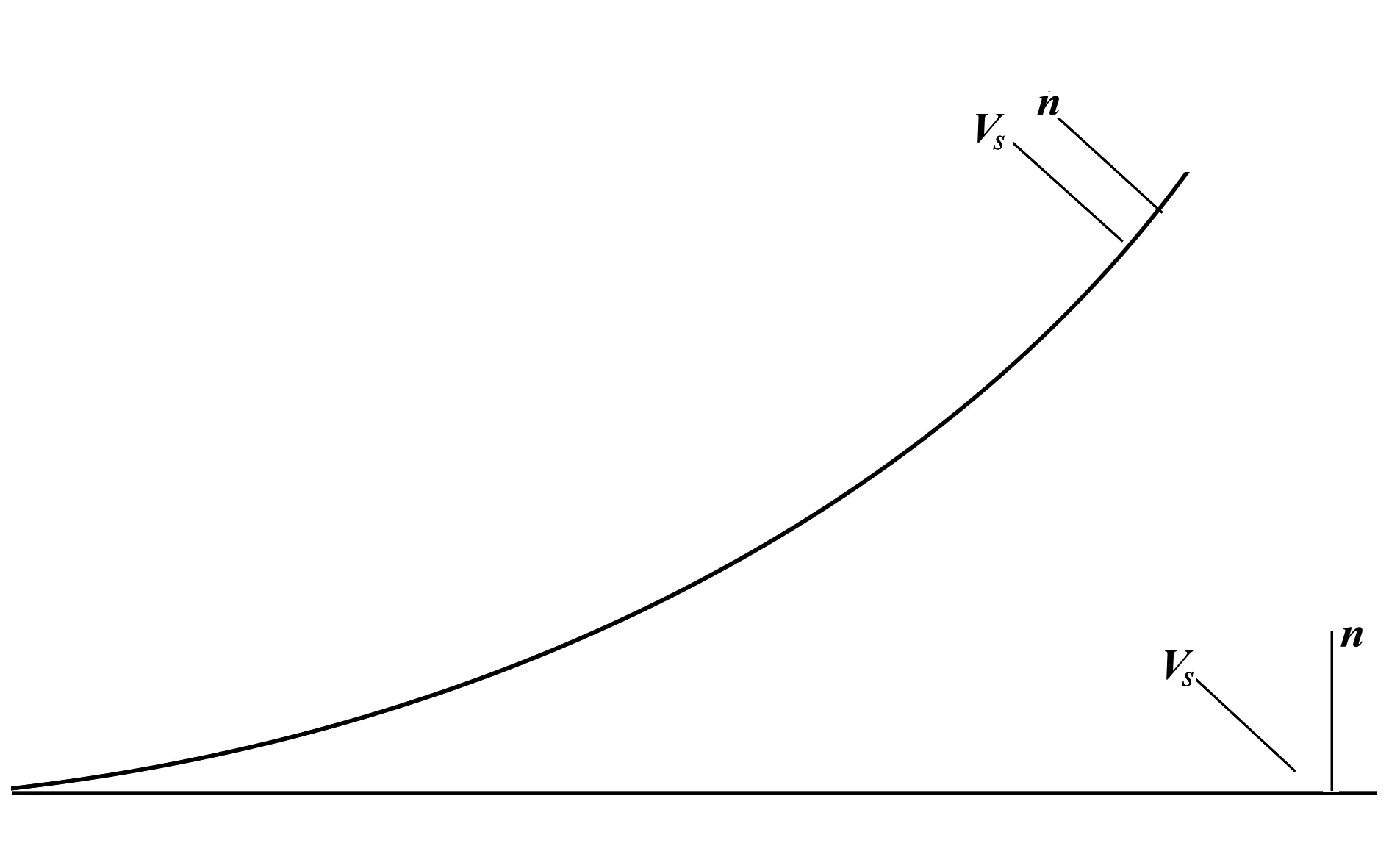
圖10 氣動(dòng)力線性與非線性差異示意圖

|Vs·n|≈|Vs|,而當(dāng)氣動(dòng)網(wǎng)格不變時(shí),運(yùn)動(dòng)速度Vs和法向量n之間存在夾角,則vn=|Vs·n|<|Vs|,且隨著變形的增大,vn減小的幅度越大。由(1)式可知,vn減小會(huì)直接導(dǎo)致渦強(qiáng)度的減小,相應(yīng)的非定常氣動(dòng)力減小,從而使計(jì)算的顫振速度偏高。所以,在結(jié)構(gòu)非線性求解中考慮氣動(dòng)面的變形是十分必要的,否則得出的結(jié)果不準(zhǔn)確,甚至可能得出相反的結(jié)果。

4 結(jié) 論

本文針對(duì)大展弦比機(jī)翼進(jìn)行了靜氣動(dòng)彈性分析與顫振分析, 并通過(guò)考慮結(jié)構(gòu)變形和內(nèi)應(yīng)力對(duì)系統(tǒng)剛度的影響, 形成了機(jī)翼幾何非線性氣動(dòng)彈性分析的實(shí)施方法。計(jì)算結(jié)果表明：

1) 隨著攻角的增大，由于結(jié)構(gòu)非線性的影響，每1°攻角產(chǎn)生的位移增量逐漸減小。

2) 攻角的增大對(duì)機(jī)翼彎曲頻率影響較小，相比之下扭轉(zhuǎn)頻率減小的幅度很大。

3) 顫振速度隨攻角的增大呈現(xiàn)出先略微增大而后減小的趨勢(shì)，說(shuō)明結(jié)構(gòu)非線性將給大展弦比機(jī)翼顫振帶來(lái)不利影響。

4) 氣動(dòng)網(wǎng)格隨平衡位置變化與保持不變2種情形下計(jì)算結(jié)果表明考慮氣動(dòng)網(wǎng)格變形的必要性。

從研究結(jié)果來(lái)看, 傳統(tǒng)的線性分析方法對(duì)于大展弦比機(jī)翼不適用,因此進(jìn)一步研究大展弦比機(jī)翼的幾何非線性氣動(dòng)彈性分析方法是很有必要的。

參考文獻(xiàn)：

[1] Dowell E. Some Recent Advances in Nonlinear Aeroelasticity: Fluid-Structure Interaction in the 21st Century[R]. AIAA-2010-3137

[2] Van Schoor M C, Von Flotow A H. Aeroelastic Characteristics of a Highly Flexible Aircraft[J]. Journal of Aircraft, 1990, 27: 901-908

[3] Patil M J. Nonlinear Aeroelastic Analysis, Flight Dynamics, and Control of a Complete Aircraft[D]. Atlanta:Georgia Institute of Technology, 1999

[4] Mayuresh J P, Dewey H H. Nonlinear Aeroelasticity and Flight Dynamics of High-Altitude Long-Endurance Aircraft[J]. Journal of Aircraft, 2001, 38: 88-94

[5] Dowell E, Edwards J, Strganac T. Nonlinear Aeroelasticity[J]. Journal of Aircraft, 2003, 40: 857-874

[6] Weihua Su, Carlos E, Cesnik S. Nonlinear Aeroelasticity of a Very Flexible Blended-Wing-Body Aircraft[J]. Journal of Aircraft,2010, 47: 1539-1553

[7] 楊智春，黨會(huì)學(xué)，李毅. 大展弦比機(jī)翼非線性氣動(dòng)彈性特性的數(shù)值模擬研究[C]∥第十一屆全國(guó)空氣彈性學(xué)術(shù)交流會(huì)，昆明：2009

Yan Zhichun, Dang Huixue, Li Yi. Research of Nonlinear Aeroelastic Characteris on High-Aspect-Ratio wing[]∥CARS-2009, Kunming, 2009 (in Chinese)

[8] 謝長(zhǎng)川，楊超. 大展弦比飛機(jī)幾何非線性氣動(dòng)彈性穩(wěn)定性的線性化方法[J]. 中國(guó)科學(xué)：技術(shù)科學(xué), 2011, 41(3): 385-393

Xie Changchuan, Yang Chao. Linearization Method of Nonlinear Aeroelastic Stability for Complete Aircraft with High-Aspect-Ratio Wings[J]. Sci China: Tech Sci, 2011, 41(3): 385-393 (in Chinese)

[9] 崔鵬,韓景龍. 基于CFD/CSD的非線性氣動(dòng)彈性分析方法[J]. 航空學(xué)報(bào), 2010, 31(3): 480-486

Cui Peng, Han Jinglong. Investigation of Nonlinear Aeroelastic Analysis Using CFD/CSD[J]. Chinese Journal of Aeronautics, 2010, 31(3): 480-486 (in Chinese)

[10] Ivan W, Chad Gibbsy S, Dowell E. Aeroelastic Analysis of a Folding Wing: Comparison of Simple and Higher Fidelity Models for a Wide Range of Fold Angles[R]. AIAA-2013-1635

[11] Bret K S, Philip S Beran. Analytical Sensitivity Analysis of an Unsteady Vortex Lattice Method for Flapping Wing Optimization[R]. AIAA-2009-2614

[12] Christopher C C, Tim F, Balakumar B. GPGPU Implementation and Benchmarking of the Unsteady Vortex Lattice Method[R]. AIAA-2013-0288, 2013