不同負載時最大功率傳輸研究

鄭焱真,任智磊，何慕威，吳援明

(電子科技大學 光電信息學院，四川 成都 611731)

實現最大功率的傳輸對于減少功率的損耗，在微弱信號的處理以及節約能源方面具有重大意義。對于一般的電路，可以將其等效為戴維南等效電路后再進行具體的研究。在一般情況下，負載往往是多種多樣的，可以是感性負載，也可以是容性負載，因此必須探討在不同負載下如何獲得最大功率。本文通過嚴格的數學推導以及具體的仿真實驗驗證得到了在負載不同情況下獲得最大功率的條件，同時，對于加入儲能元件構成的網絡以及理想變壓器來使負載獲得最大功率也進行了較為簡單的探究。

1 不同負載時最大功率的理論推導

將內部電路等效成圖1電路，然后討論ab端口外接不同負載時負載獲得的最大功率的問題，最后根據歐姆定律求出負載兩端的電壓及電流。根據有功功率的表達式進行推導[1-4]。負載為ZL=RL+jXL=|ZL|·(cosθ+jsinθ),RL為外接負載電阻，戴維南等效阻抗Zo=Ro+jXo=|Zo|(cosφ+j sinφ)，在不同情況下選擇不同的形式。

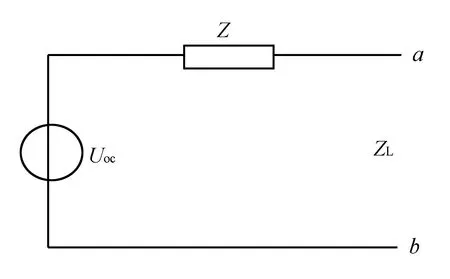
圖1 內部電路的等效電路

1.1 負載的實部和虛部都可變

此時負載ZL獲得的功率[5]為

若負載獲得最大功率，則有Xo+XL=0，也就是XL=-Xo；此時，

當Ro=RL時就是常說的共軛匹配。容易知道，若負載共軛匹配時，此時負載獲得的功率在理論上能獲得最大功率。因此當XL=-Xo且Ro=RL時，負載獲得的最大功率[6]為

(1)

1.2 負載的實部可變而虛部不變

此時負載ZL獲得的功率為

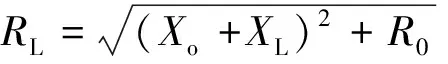
(2)

1.3 負載的虛部可變而實部不變

此時負載ZL獲得的功率為

P為XL的函數。P取得最大時，顯然有Xo+XL=0，即XL=-Xo[5]，所獲得的最大功率為

(3)

1.4 負載的模及相位都可變

本模型重在討論戴維南等效內阻與外接負載同為容性負載或者同為感性負載的情況，意即后文中的θ恒大于等于零或恒小于等于零的情況，此情況對于實際應用具有重要意義。

此時有

令

可知：|zL|2=|zo|2，則有

因此容易得到以下結論：

因此負載獲得的最大功率的條件是|zL|2=|zo|2即阻抗匹配，且負載為純電阻，所獲得的最大功率為

(4)

1.5 負載的模可變而相位不變

此時負載ZL獲得的功率為

(5)

1.6 負載的相位可變而模不變

此時負載ZL獲得的功率為

令

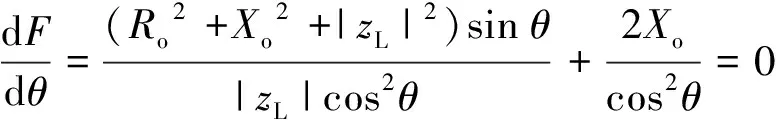
由極值的第一充分條件[8]，F取得最小值，因此，P有最大值。

(6)

如果負載的模與戴維南等效電路內部阻抗模的大小相等，容易知道上式θ等于戴維南等效電路內部阻抗阻抗角[9]。

1.7 加入儲能元件構成的匹配網絡

假設加入一個電感L與電容C構成的匹配網絡(見圖2)，戴維南等效內阻Z0以及負載R均為純電阻的情況。如果滿足共軛匹配的條件，顯然負載獲得最大功率，經過簡單的數學推導，得到以下2個最簡單的等式：

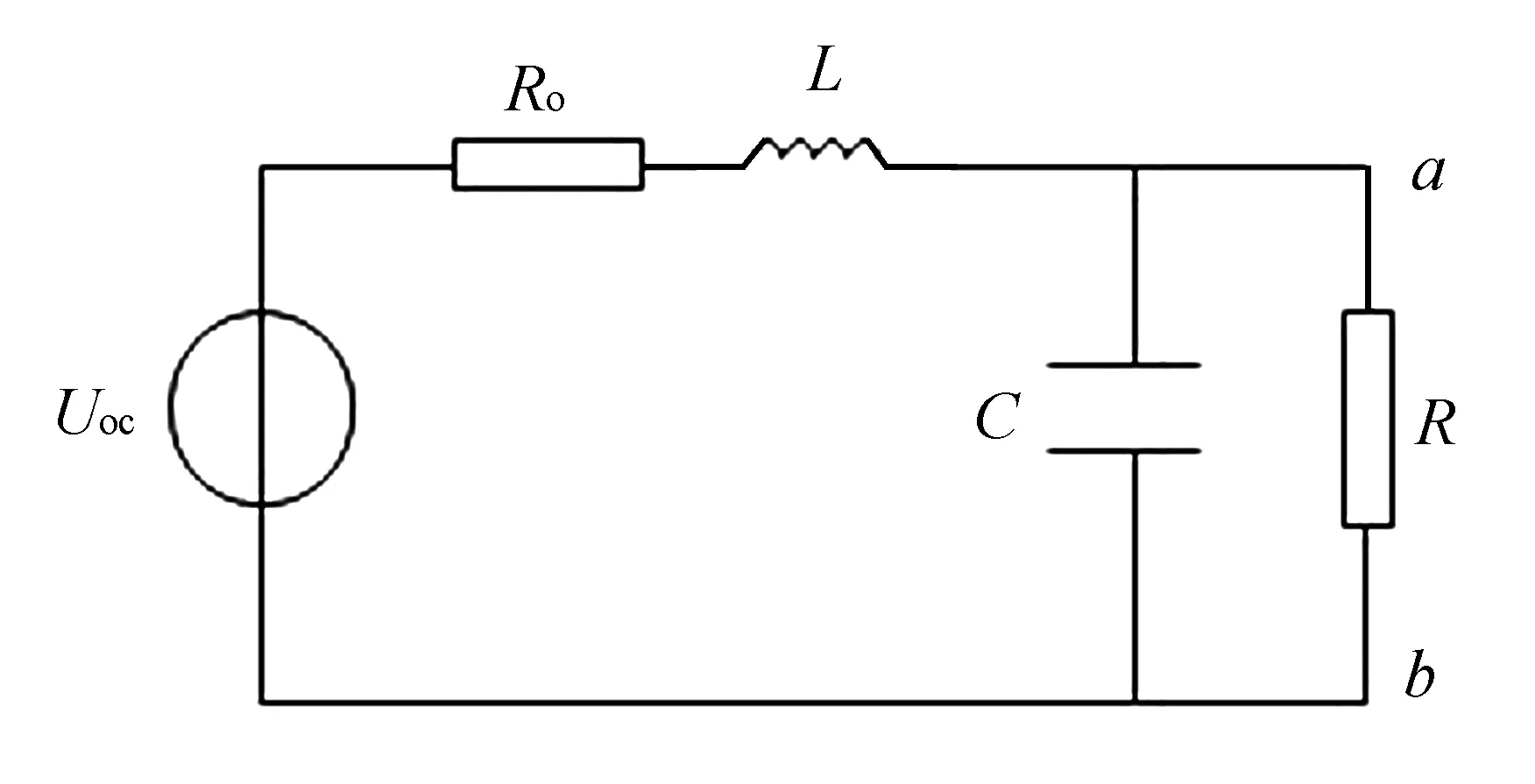
圖2 匹配網絡

解這兩個式子即可得到L、C、R與Ro的關系，得到匹配網絡需要滿足的關系為

1.8 加入理想變壓器

對于該種情況，仍然只討論負載以及戴維南等效阻抗仍僅為純電阻的情況。由于理想變壓器不吸收功率并且具有阻抗變換的作用，其公式為R′=n2R,n為變壓器匝數比。當戴維南等效阻抗與負載不為負電阻時，總可以找到合適的n使負載滿足共軛匹配的條件，讓負載獲得最大功率[10]。

由于此種方法成本較高并且變壓器體積較大，不適于在電子電路中使用。

2 部分結論的仿真驗證

Multisim軟件是NI公司發布的交互式SPICE仿真和電路分析的軟件仿真[11]。實驗采用Multisim12.0仿真軟件(以下均使用“仿真軟件”)，利用瓦特計測量功率[12-14]。

2.1 負載的實部和虛部都可變

在仿真軟件中搭載如圖3所示的電路。通過調節可變電阻及可變電感的大小來實現負載的實部及虛部單獨可變，并且記錄負載不同時瓦特計測量功率的大小。

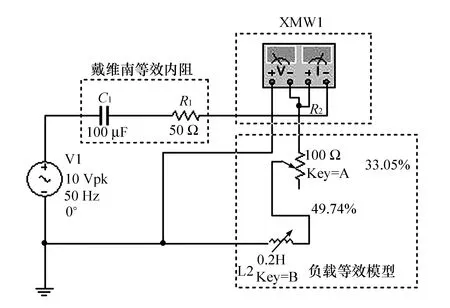
圖3 負載的實部和虛部單獨可變仿真電路

根據1.1中的結論，當且僅當外部負載阻抗為(50+j31.85)Ω時，外部負載獲得最大功率，對應的電感與電阻的百分比分別為50.5%和50%，最大功率為250 mW。

仿真實驗數據見表1。由實驗數據可知，在電感與電阻百分比分別為50.5%、50%時有最大功率，為250.00 mW。

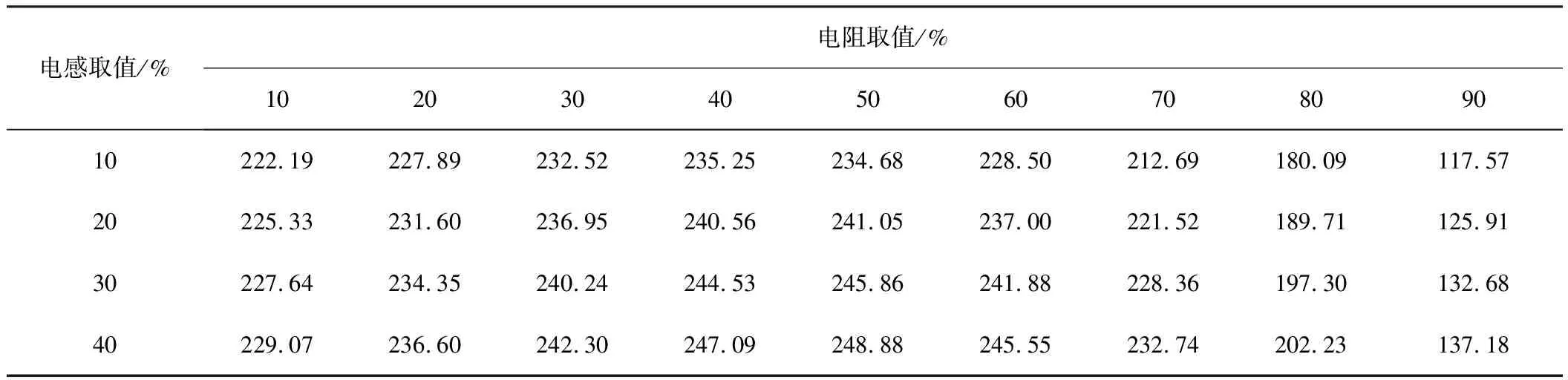
表1 負載的實部和虛部單獨可變時仿真實驗數據 mW

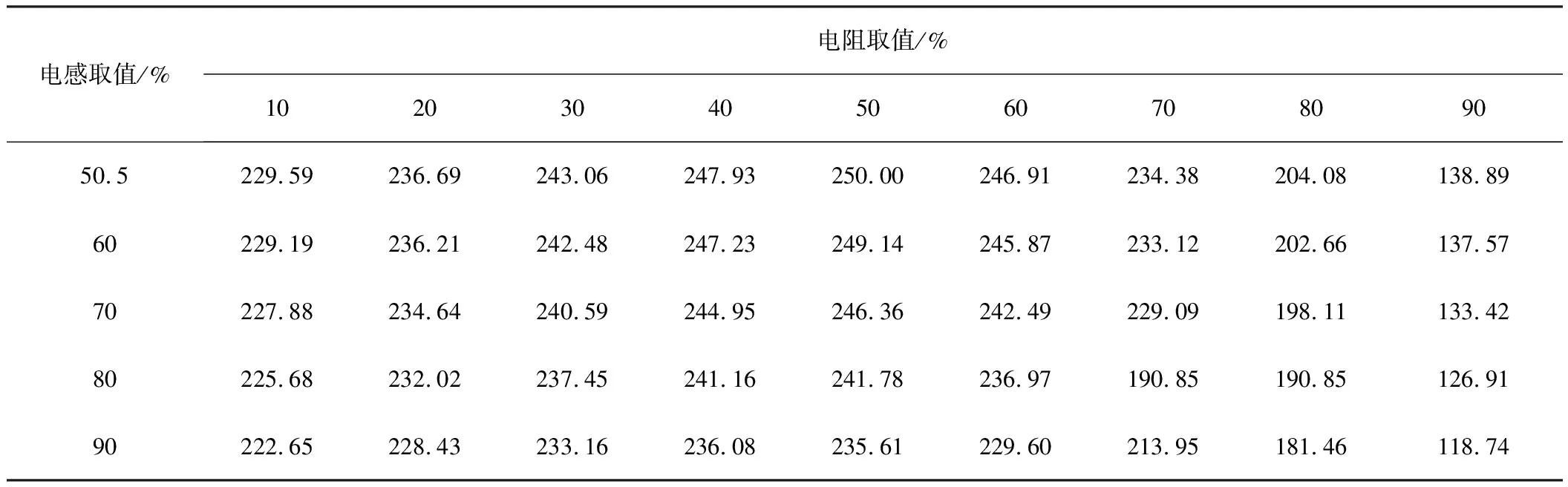
表1(續) mW

對于負載的實部可變而虛部不變、負載的虛部可變而實部不變的仿真實驗與本實驗的方案類似。

2.2 負載的模和相位單獨可變

本文僅就戴維南等效內阻為感性負載的情況進行分析。在仿真軟件中搭載如圖4所示的電路，通過改變可變電阻與可變電感的百分比來改變負載的模及相位的大小，記錄百分比不同時負載瓦特計示數。根據2.4中的結論，當負載為8.9 Ω時功率存在最大值，即可變電感與可變電阻的百分比分別為0%與85.95%時存在最大值，最大功率為1.507 W。

圖4 感性負載且負載的模和相位可變的仿真電路

仿真結果見表2,由實驗結果可知，負載在可變電感與可變電阻的百分比分別為0%與85.95%時取得最大功率，為1.507 W，與理論結果相一致。

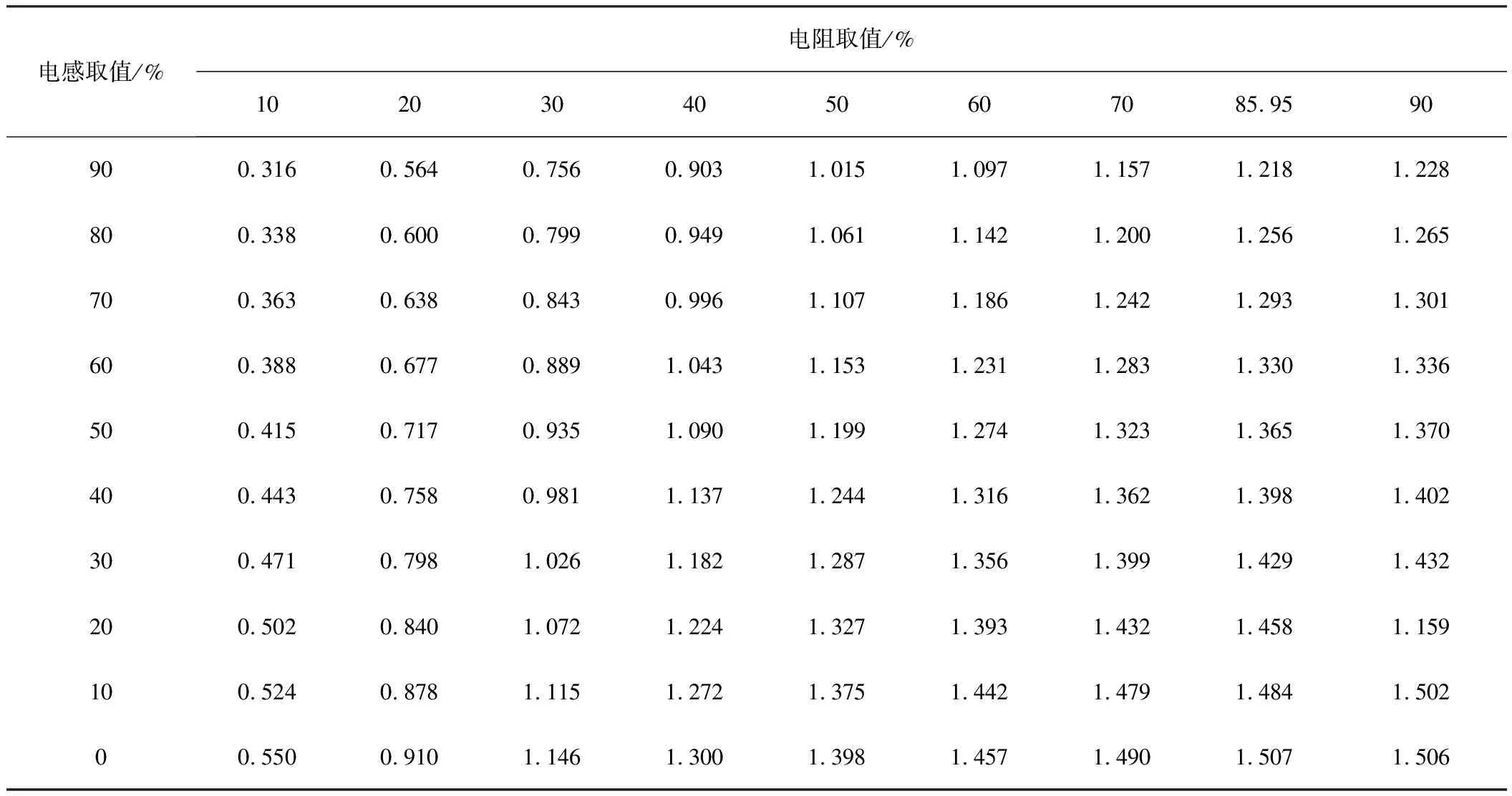
表2 負載的模和相位單獨可變時仿真實驗數據 W

對于戴維南等效內阻為容性負載的情況，仍然可以用類似的方法做分析。

2.3 負載的模可變而相位不變

在仿真軟件中搭載如圖5所示的電路，通過控制可變電感及可變電阻所占電阻大小的百分比來控制負載模的大小，由于相位不能變，故應保持可變電感及可變電阻的百分比比值不發生改變。

根據1.5中的結論，當可變電感與可變電阻的百分比都為50%時取得最大功率，最大功率為12.5 W。

仿真實驗結果見表3。由仿真的結果可知，可變電阻與可變電感的百分比均為50%時取得最大功率，為12.500 W與理論推導的結果一致。

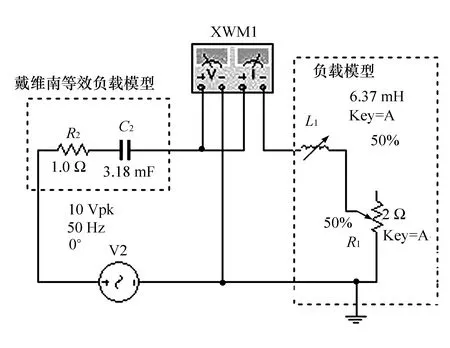
圖5 負載的模可變而相位不變的仿真電路

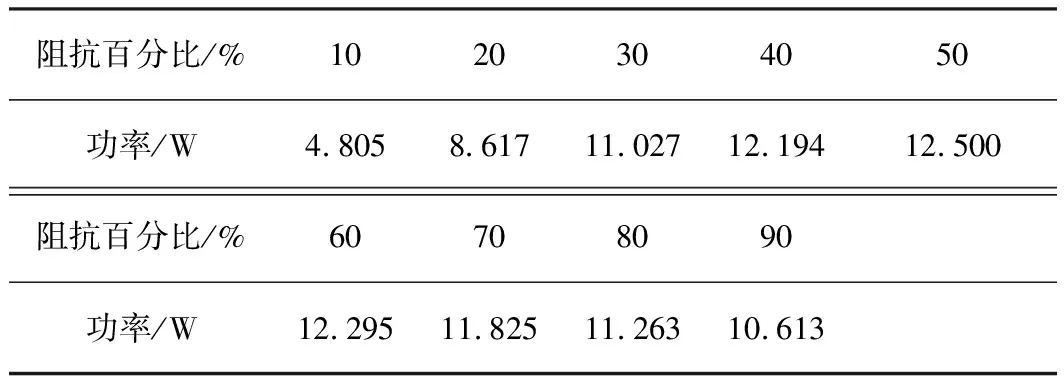
表3 負載的模可變而相位不變時仿真實驗數據

2.4 負載的相位可變而模不變

該種情況本文不再詳細驗證，只給出具體思路。不妨假設戴維南等效內阻為容性負載的情況，而負載為感性負載。由于模不改變，因此，可通過改變可變電阻及可變電感的百分比來改變其相位的大小，此處假設模的大小為|ZL|，可變電阻(R1)的百分比為x，可變電感(L1)的百分比為y，由于保證模的大小不發生改變，因此有如下恒等式成立：(2πfL1y)2+(R1x)2=|ZL|，找出x與y的關系，通過簡單的仿真，即可驗證理論推導結果的正確性。

3 結束語

實際應用中的負載多種多樣，但是容性負載與感性負載是兩種重要的負載模型，討論這兩種抽象的負載模型對于工程上的應用具有重要價值。但正是因為實際情況的復雜，在很多情況下不能滿足共軛匹配的理想狀況，因此對于其他一些情況的討論就顯得有必要。Multisim仿真提供了一個十分便捷的科學實驗平臺[15],可以方便計算有關問題。本文通過理論推導以及Multisim仿真驗證，對于實際工程應用中的復雜情況進行了初步探討，得到在負載不同情況下負載獲得最大功率的條件(例如共軛匹配和阻抗匹配)，這些結論對電子工程中微弱信號的處理以及能源的節約和能源充分利用方面具有重要意義。

對于加入理想變壓器及匹配網絡的情況，本文僅僅進行了簡單的討論，但是加入匹配網絡對于實際應用具有重要的價值。這種方法不僅不會消耗功率，同時可讓負載實現共軛匹配以獲得最大功率。

本文僅僅對集中參數電路最大功率進行討論，同時得到的也是在較低頻率情況下的最大功率傳輸，對于頻率較高的情況未加涉及。

[1] 胡翔駿.電路分析[M].2版.北京：高等教育出版社，2007：164-169,409-412.

[2] 狄蘇爾C A，葛守仁.電路基本理論[M].林爭輝,譯.北京：人民教育出版社，1979.

[3] 顏秋容,李妍,曹娟.最大功率傳輸定理應用的思考[J].電氣電子教學學報,2007,29(3):51-53.

[4] 劉秀成，黃松嶺，于歆杰，等.關于最大功率傳輸問題的討論[J].電氣電子教學學報,2008,30(1):19-22.

[5] 李瀚蓀.電路分析基礎(下冊)[M].4版.北京：高等教育出版社，2006：90-93.

[6] 周茜.電路分析基礎[M].北京:電子工業出版社，2010.

[7] 嚴朝雄，戴亞文，徐志花.最大功率傳輸問題的研究[J].黃岡師范學院學報，2010，30(6)：53-56.

[8] 傅英定，謝云蓀.微積分(上冊)[M].2版.北京：高等教育出版社，2009.

[9] 左全生.負載阻抗ZL受限制情況下的最大功率傳輸的研究[J].常州工學院學報,2008,21(2):32-35.

[10] 王全保.電子變壓器手冊[M].北京：科學出版社，1983.

[11] National Instruments Cooperation.Multisim MCU Module User Gudie[Z].

[12] 尹勇,李林凌.Multisim 電路仿真入門與進階[M].北京：科學出版社，2005.

[13] 蔣卓勤,黃天錄,鄧玉元.Multisim及其在電子設計中的應用[J].2版.西安：西安電子科技大學出版社，2011.

[14] 酆達,姜珊.感性負載功率因數提高的 Multisim2001仿真分析[J].實驗科學與技術,2010,8(2):5-14.

[15] 付揚.Multisim仿真在電工電子實驗中的應用[J].實驗室研究與探索，2011，30(4):120-122,126.